人教A数学必修二 直线平面平行的判定及其性质学案 4页

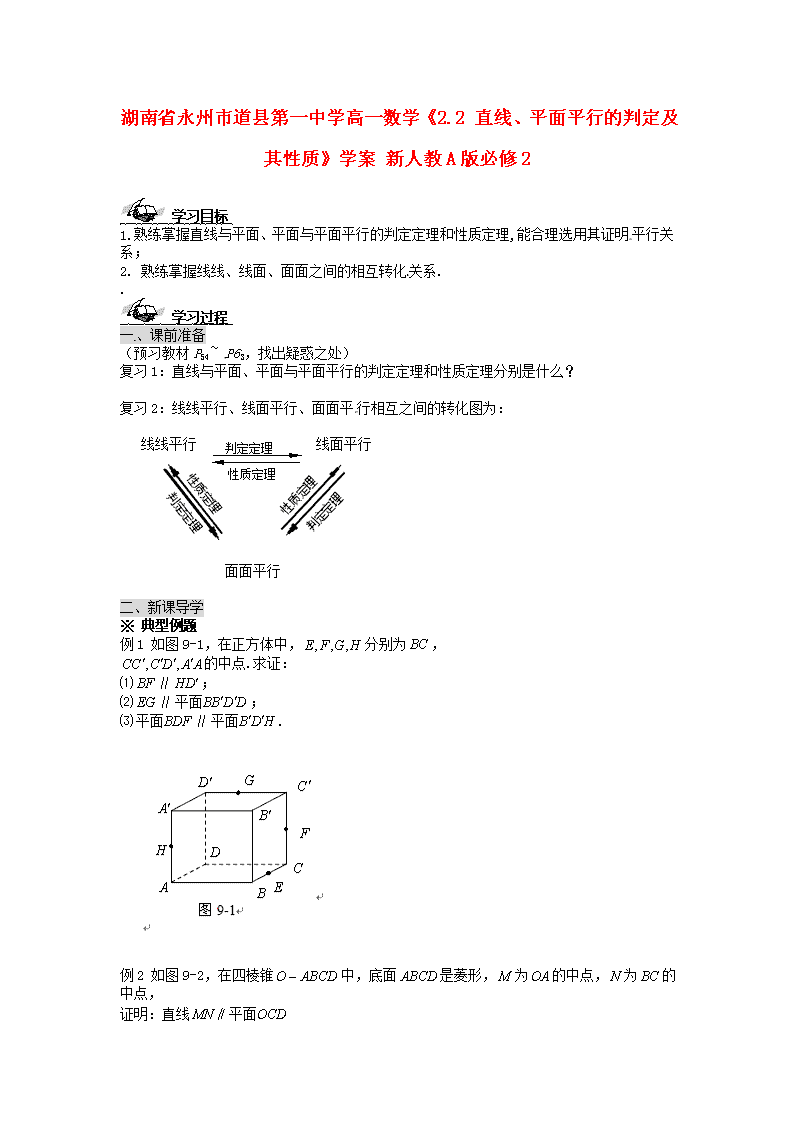
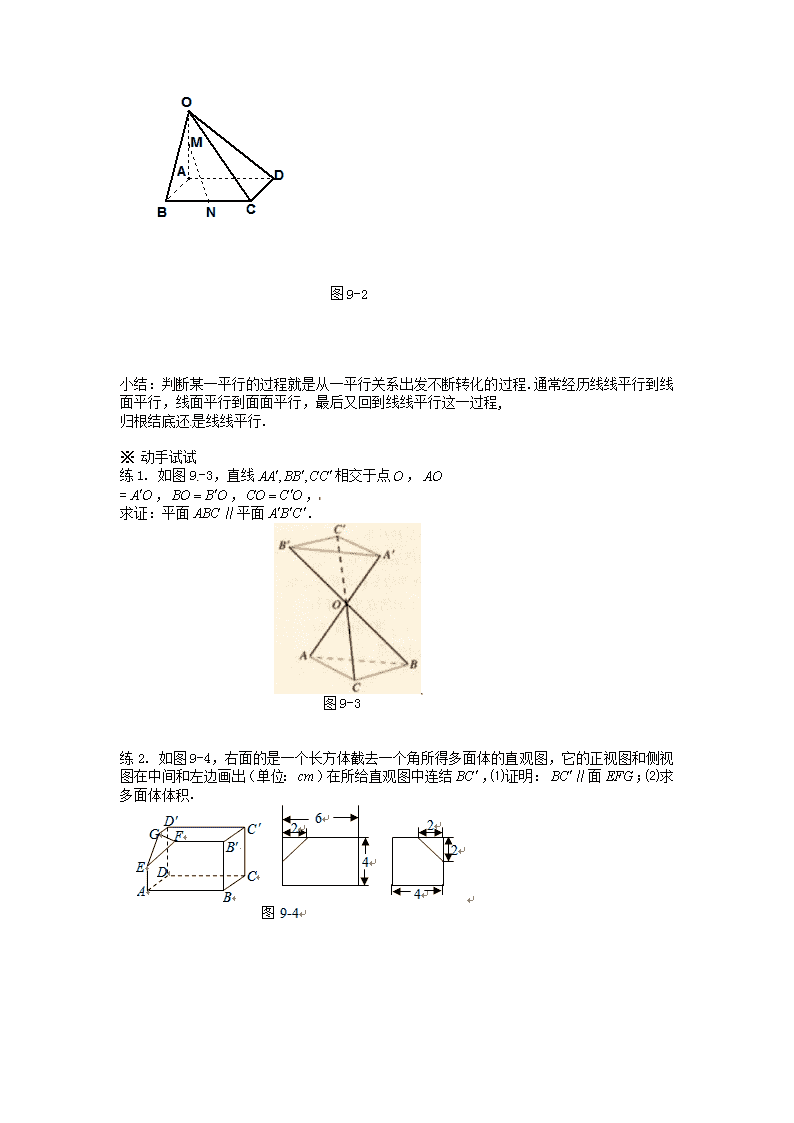
湖南省永州市道县第一中学高一数学《2.2 直线、平面平行的判定及其性质》学案 新人教A版必修2‎ ‎ 学习目标 ‎ ‎1. 熟练掌握直线与平面、平面与平面平行的判定定理和性质定理,能合理选用其证明平行关系；‎ ‎2. 熟练掌握线线、线面、面面之间的相互转化关系.‎ ‎.‎ ‎ 学习过程 ‎ 一、课前准备 ‎（预习教材P54~ P63，找出疑惑之处）‎ 复习1：直线与平面、平面与平面平行的判定定理和性质定理分别是什么？‎ 判定定理 性质定理 复习2：线线平行、线面平行、面面平行相互之间的转化图为：‎ 线线平行 线面平行 面面平行 ‎ ‎ ‎ 二、新课导学 ‎※ 典型例题 例1 如图9-1，在正方体中，分别为，‎ 的中点.求证：‎ ‎⑴∥；‎ ‎⑵∥；‎ ‎⑶∥.‎ ‎ ‎ 例2 如图9-2，在四棱锥中，底面是菱形，为的中点，为的中点，‎ 证明：直线 图9-2‎ 小结：判断某一平行的过程就是从一平行关系出发不断转化的过程.通常经历线线平行到线面平行，线面平行到面面平行，最后又回到线线平行这一过程,‎ 归根结底还是线线平行.‎ ‎※ 动手试试 练1. 如图9-3，直线相交于点，‎ ‎=，，，‎ 求证：平面∥平面.‎ 图9-3‎ 练2. 如图9-4，右面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在中间和左边画出（单位：）在所给直观图中连结，⑴证明：面；⑵求多面体体积.‎ 练3. 如图9-5，∥∥，直线与分别交,‎ ‎,于点和点，求证：.‎ 图9-5‎ 三、总结提升 ‎※ 学习小结 线面平行、面面平行判定定理和性质定理的熟练运用；平行关系的熟练转化.‎ ‎※ 知识拓展 ‎ 在立体几何中，证明图形的存在性或唯一性时，常常运用反证法和同一法.‎ 反证法：先提出和原命题中的结论相反的假定，然后从这个假定中得出和已知条件相矛盾的结果，这样就否定了原来的假定而肯定原命题.‎ 同一法：欲证图形有某种特性时，可另作一个具有同样特征的图形，再证明所作图形和已知条件中的图形是同一个.如果不是同一个，则与某公理或定理相矛盾.‎ ‎ 学习评价 ‎ ‎※ 自我评价 你完成本节导学案的情况为（ ）.‎ ‎ A. 很好 B. 较好 C. 一般 D. 较差 ‎※ 当堂检测（时量：5分钟 满分：10分）计分：‎ ‎1. 下列条件能推出平面∥平面的是（ ）.‎ ‎ A.存在一条直线，∥，∥‎ ‎ B.存在一条直线，，∥‎ ‎ C.存在两条平行直线，，∥，‎ ‎∥‎ ‎ D. 存在两条异面直线，，∥，‎ ‎∥‎ ‎2. 设为两条直线，为两个平面，下列三个结论正确的有（ ）个.‎ ‎①若与所成的角相等，则∥‎ ‎②若∥，∥，∥，则∥‎ ‎③若，∥，则∥‎ ‎ A.0 B‎.1 C.2 D.3‎ ‎3. 和是夹在平行平面间的两条异面线段，分别是它们的中点，则和（ ）.‎ ‎ A.平行 B.相交 C.垂直 D.不能确定 ‎4. 在由正方体棱的中点组成的直线中，和正方体的一个对角面平行的直线有_______条.‎ ‎5. ,试在横线上写出条件，使得 ‎∥.____________________________________‎ ‎ 课后作业 ‎ ‎1. 如图9-6，四边形是矩形，是、‎ 的中点，求证：∥面.‎ ‎2. 如图9-7，在正三棱柱中，是的中点，‎ 求证：∥面.‎ 图9-8‎