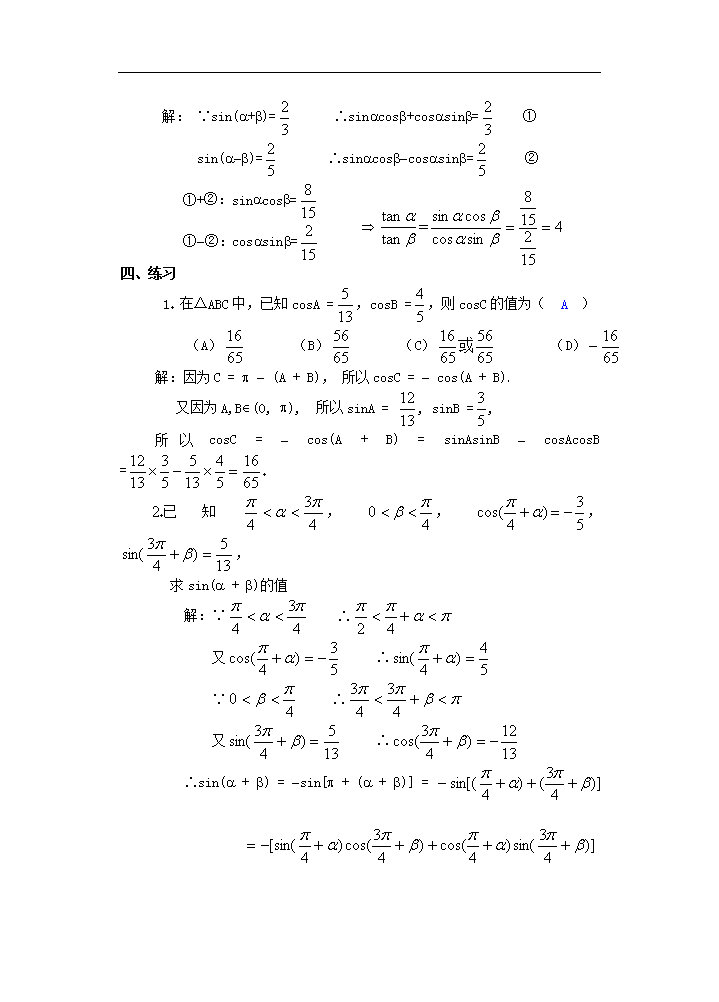高中数学必修1教案：第四章（第13课时）两角和差的正弦余弦正切（2） 4页

课 题：46 两角和与差的正弦、余弦、正切（2） 教学目的： 能由两角和的余弦公式推导出两角和的正弦公式，并进而推得两角和的正 弦公式，并运用进行简单的三角函数式的化简、求值和恒等变形 教学重点： 由两角和的余弦公式推导出两角和的正弦公式 教学难点： 进行简单的三角函数式的化简、求值和恒等变形 授课类型：新授课 课时安排：1 课时 教 具：多媒体、实物投影仪 教学过程： 一、复习引入： 1．两角和与差的余弦公式:  sinsincoscos)cos(   sinsincoscos)cos(  2．求 cos75的值 解：cos75=cos(45+30)=cos45cos30sin45sin30 = 4 26 2 1 2 2 2 3 2 2  3．计算：cos65cos115cos25sin115 解：原式= cos65cos115sin65sin115=cos(65+115)=cos180=1 4 计算：cos70cos20+sin110sin20 原式=cos70cos20+sin70sin20=cos(70+20)=0 5．已知锐角,满足 cos= 5 3 cos(+)= 13 5 求 cos 解：∵cos= 5 3 ∴sin= 5 4 又∵cos(+)= 13 5 <0 ∴+为钝角 ∴sin(+)= 13 12 ∴cos=cos[(+)]=cos(+)cos+sin(+)sin = 65 33 5 4 13 12 5 3 13 5  （角变换技巧） 二、讲解新课： 两角和与差的正弦 1 推导 sin(+)=cos[ 2  (+)]=cos[( 2  )] =cos( 2  )cos+sin( 2  )sin =sincos+cossin 即：  cossincossin)sin(  （S+） 以代得：  cossincossin)sin(  （S） 2 公式的分析，结构解剖，嘱记 三、讲解范例： 例 1 不查表，求下列各式的值： 1 sin75 2 sin13cos17+cos13sin17 解：1原式= sin(30+45)= sin30cos45+cos30sin45 = 4 62 2 2 2 3 2 2 2 1  2原式= sin(13+17)=sin30= 2 1 例 2 求证：cos+ 3 sin=2sin( 6  +) 证一（构造辅助角）： 左边=2( 2 1 cos+ 2 3 sin)=2(sin 6  cos+cos 6  sin) =2sin( 6  +)=右边 证二：右边=2(sin 6  cos+cos 6  sin)=2( 2 1 cos+ 2 3 sin) = cos+ 3 sin=左边 例 3 已知 sin(+)= 3 2 ,sin()= 5 2 求   tan tan 的值 解： ∵sin(+)= 3 2 ∴sincos+cossin= 3 2 ① sin()= 5 2 ∴sincoscossin= 5 2 ② ①+②：sincos= 15 8 ①②：cossin= 15 2 四、练习 1 在△ABC 中，已知 cosA = 13 5 ，cosB = 5 4 ，则 cosC 的值为（ A ） （A） 65 16 （B） 65 56 （C） 65 56 65 16 或 （D） 65 16 解：因为 C =   (A + B)， 所以 cosC =  cos(A + B) 又因为 A,B(0, ), 所以 sinA = 13 12 , sinB = 5 3 , 所以 cosC =  cos(A + B) = sinAsinB  cosAcosB = 65 16 5 4 13 5 5 3 13 12  2 已知 4 3 4   ， 40   ， 5 3)4cos(  ， 13 5)4 3sin(   ， 求 sin( + )的值 解：∵ 4 3 4   ∴   42 又 5 3)4cos(  ∴ 5 4)4sin(  ∵ 40   ∴   4 3 4 3 又 13 5)4 3sin(   ∴ 13 12)4 3cos(   ∴sin( + ) = sin[ + ( + )] = )]4 3()4sin[(   )]4 3sin()4cos()4 3cos()4[sin(   65 63]13 5 5 3)13 12(5 4[  五、小结 两角和与差的正弦、余弦公式及一些技巧“辅助角”“角变换”“逆 向运用公式”    tan tan = 4 15 2 15 8 sincos cossin   六、课后作业： 1 已知 sin + sin = 2 2 ，求 cos + cos的范围 解：设 cos + cos = t， 则(sin + sin)2 + (cos + cos)2= 2 1 + t2 ∴2 + 2cos(  ) = 2 1 + t2 即 cos(  ) = 2 1 t2  4 3 又∵1≤cos(  )≤1 ∴1≤ 2 1 t2  4 3 ≤1 ∴ 2 14 ≤t≤ 2 14 2 已知 sin(+) = 2 1 ，sin() = 10 1 ，求   tan tan 的值 解：由题设：                5 1sincos 10 3cossin 10 1sincoscossin 2 1sincoscossin     从而： 2 3510 3 sincos cossin tan tan      或设：x =   tan tan ∵ 5)sin( )sin(     ∴ 51 1 1tan tan 1tan tan tantan tantan coscos )sin( coscos )sin(        x x           ∴x = 2 3 即   tan tan = 2 3 七、板书设计（略） 八、课后记：