高中数学必修1教案第二章 2_2_2 第2课时对数函数及其性质的应用 10页

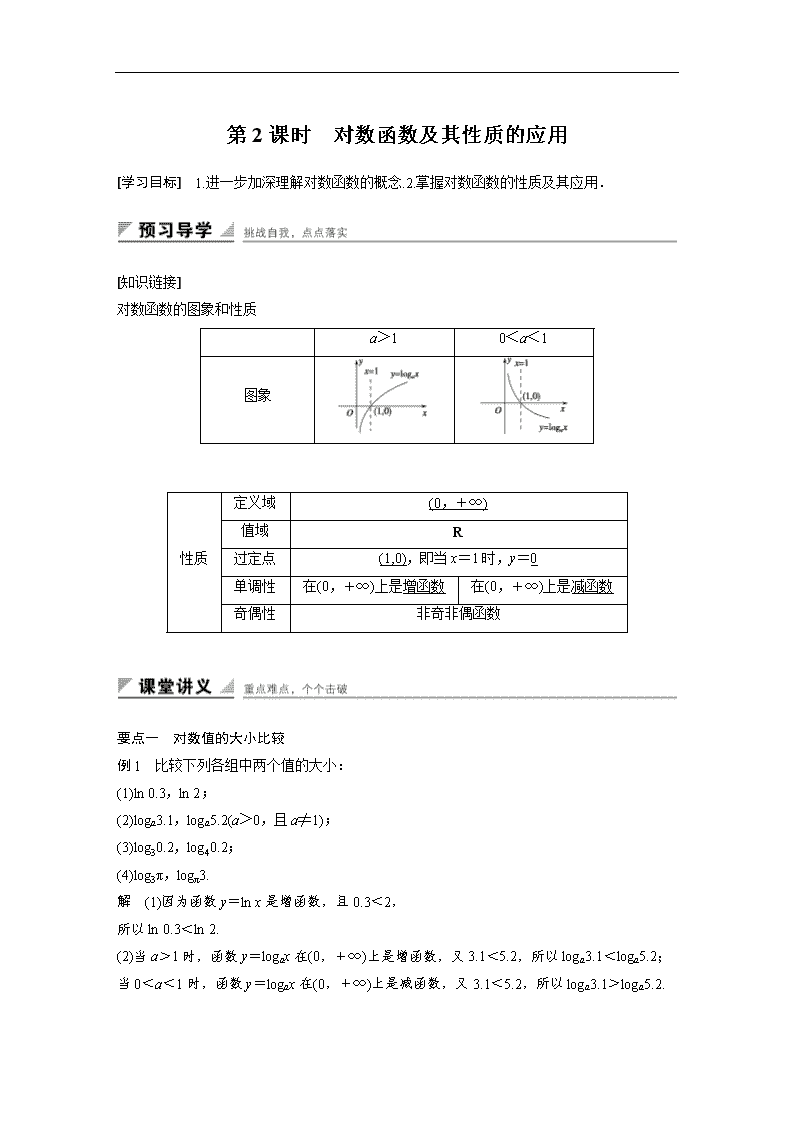
第2课时　对数函数及其性质的应用 ‎[学习目标]　1.进一步加深理解对数函数的概念.2.掌握对数函数的性质及其应用．‎ ‎[知识链接]‎ 对数函数的图象和性质 a＞1‎ ‎0＜a＜1‎ 图象 性质 定义域 ‎(0，＋∞)‎ 值域 R 过定点 ‎(1,0)，即当x＝1时，y＝0‎ 单调性 在(0，＋∞)上是增函数 在(0，＋∞)上是减函数 奇偶性 非奇非偶函数 要点一　对数值的大小比较 例1　比较下列各组中两个值的大小：‎ ‎(1)ln 0.3，ln 2；‎ ‎(2)loga3.1，loga5.2(a＞0，且a≠1)；‎ ‎(3)log30.2，log40.2；‎ ‎(4)log3π，logπ3.‎ 解　(1)因为函数y＝ln x是增函数，且0.3＜2，‎ 所以ln 0.3＜ln 2.‎ ‎(2)当a＞1时，函数y＝logax在(0，＋∞)上是增函数，又3.1＜5.2，所以loga3.1＜loga5.2；‎ 当0＜a＜1时，函数y＝logax在(0，＋∞)上是减函数，又3.1＜5.2，所以loga3.1＞loga5.2.‎ ‎(3)方法一　因为0＞log0.23＞log0.24，所以＜，即log30.2＜log40.2.‎ 方法二　如图所示，‎ 由图可知log40.2＞log30.2.‎ ‎(4)因为函数y＝log3x是增函数，且π＞3，所以log3π＞log33＝1.‎ 同理，1＝logππ＞logπ3，所以log3π＞logπ3.‎ 规律方法　比较对数式的大小，主要依据对数函数的单调性．‎ ‎1．若底数为同一常数，则可由对数函数的单调性直接进行比较．‎ ‎2．若底数为同一字母，则根据底数对对数函数单调性的影响，对底数进行分类讨论．‎ ‎3．若底数不同，真数相同，则可以先用换底公式化为同底后，再进行比较，也可以利用顺时针方向底数增大的规律画出函数的图象，再进行比较．‎ ‎4．若底数与真数都不同，则常借助1,0等中间量进行比较．‎ 跟踪演练1　(1)设a＝log32，b＝log52，c＝log23，则(　　)‎ A．a＞c＞b B．b＞c＞a C．c＞b＞a D．c＞a＞b ‎(2)已知a＝log23.6，b＝log43.2，c＝log43.6，则(　　)‎ A．a＞b＞c B．a＞c＞b C．b＞a＞c D．c＞a＞b 答案　(1)D　(2)B 解析　(1)a＝log32＜log33＝1；c＝log23＞log22＝1，‎ 由对数函数的性质可知log52＜log32，‎ ‎∴b＜a＜c，故选D.‎ ‎(2)a＝log23.6＝log43.62，函数y＝log4x在(0，＋∞)上为增函数，3.62＞3.6＞3.2，所以a＞c＞b，故选B.‎ 要点二　对数函数单调性的应用 例2　求函数y＝log(1－x2)的单调增区间，并求函数的最小值．‎ 解　要使y＝log(1－x2)有意义，则1－x2＞0，‎ ‎∴x2＜1，则－1＜x＜1，因此函数的定义域为(－1,1)．‎ 令t＝1－x2，x∈(－1,1)．‎ 当x∈(－1,0]时，x增大，t增大，y＝logt减小，‎ ‎∴x∈(－1,0]时，y＝log(1－x2)是减函数；‎ 当x∈[0,1)时，y＝log(1－x2)是增函数．‎ 故函数y＝log(1－x2)的单调增区间为[0,1)，且函数的最小值ymin＝log(1－02)＝0.‎ 规律方法　1.求形如y＝logaf(x)的函数的单调区间，一定树立定义域优先意识，即由f(x)＞0，先求定义域．‎ ‎2．求此类型函数单调区间的两种思路：(1)利用定义求证；(2)借助函数的性质，研究函数t＝f(x)和y＝logat在定义域上的单调性，从而判定y＝logaf(x)的单调性．‎ 跟踪演练2　(1)函数f(x)＝|logx|的单调递增区间是(　　)‎ A. B．(0,1]‎ C．(0，＋∞) D．[1，＋∞)‎ ‎(2)设函数f(x)＝则满足f(x)≤2的x的取值范围是(　　)‎ A．[－1,2] B．[0,2]‎ C．[1，＋∞) D．[0，＋∞)‎ 答案　(1)D　(2)D 解析　(1)f(x)＝当x≥1时，t＝logx是减函数，f(x)＝－logx是增函数．‎ ‎∴f(x)的单调增区间为[1，＋∞)．‎ ‎(2)f(x)≤2⇔或⇔0≤x≤1或x＞1，故选D.‎ 要点三　对数函数的综合应用 例3　已知函数f(x)＝loga(a＞0且a≠1)，‎ ‎(1)求f(x)的定义域；‎ ‎(2)判断函数的奇偶性和单调性．‎ 解　(1)要使此函数有意义，‎ 则有或 解得x＞1或x＜－1，‎ 此函数的定义域为(－∞，－1)∪(1，＋∞)．‎ ‎(2)f(－x)＝loga＝loga ‎＝－loga＝－f(x)．‎ 又由(1)知f(x)的定义域关于原点对称，‎ ‎∴f(x)为奇函数．‎ f(x)＝loga＝loga(1＋)，‎ 函数u＝1＋ 在区间(－∞，－1)和区间(1，＋∞)上单调递减．‎ 所以当a＞1时，f(x)＝loga在(－∞，－1)，(1，＋∞)上递减；‎ 当0＜a＜1时，f(x)＝loga在(－∞，－1)，(1，＋∞)上递增．‎ 规律方法　1.判断函数的奇偶性，首先应求出定义域，看是否关于原点对称．‎ ‎2．求函数的单调区间有两种思路：(1)易得到单调区间的，可用定义法来求证；(2)利用复合函数的单调性求得单调区间．‎ 跟踪演练3　已知函数f(x)＝loga(a＞0，a≠1，m≠1)是奇函数．‎ ‎(1)求实数m的值；‎ ‎(2)探究函数f(x)在(1，＋∞)上的单调性．‎ 解　(1)由已知条件得f(－x)＋f(x)＝0对定义域中的x均成立．‎ ‎∴loga＋loga＝0，‎ 即·＝1，‎ ‎∴m2x2－1＝x2－1对定义域中的x均成立．‎ ‎∴m2＝1，即m＝1(舍去)或m＝－1.‎ ‎(2)由(1)得f(x)＝loga.‎ 设t＝＝＝1＋，‎ ‎∴当x1＞x2＞1时，‎ t1－t2＝－＝＜0，‎ ‎∴t1＜t2.‎ 当a＞1时，logat1＜logat2，即f(x1)＜f(x2)，‎ ‎∴当a＞1时，f(x)在(1，＋∞)上是减函数．‎ 同理当0＜a＜1时，f(x)在(1，＋∞)上是增函数．‎ ‎1．函数y＝ln x的单调递增区间是(　　)‎ A．[e，＋∞) B．(0，＋∞)‎ C．(－∞，＋∞) D．[1，＋∞)‎ 答案　B 解析　函数y＝ln x的定义域为(0，＋∞)，其在(0，＋∞)上是增函数，故该函数的单调递增区间为(0，＋∞)．‎ ‎2．设a＝log54，b＝(log53)2，c＝log45，则(　　)‎ A．a＜c＜b B．b＜c＜a C．a＜b＜c D．b＜a＜c 答案　D 解析　∵1＝log55＞log54＞log53＞log51＝0，‎ ‎∴1＞a＝log54＞log53＞b＝(log53)2.‎ 又∵c＝log45＞log44＝1.∴c＞a＞b.‎ ‎3．函数f(x)＝的定义域是(　　)‎ A．(1，＋∞) B．(2，＋∞)‎ C．(－∞，2) D．(1,2]‎ 答案　D 解析　由题意有解得1＜x≤2.‎ ‎4．函数f(x)＝的值域为________．‎ 答案　(－∞，2)‎ 解析　当x≥1时，logx≤log1＝0，∴当x≥1时，f(x)≤0.当x＜1时，0＜2x＜21，即0＜f(x)＜2.因此函数f(x)的值域为(－∞，2)．‎ ‎5．函数f(x)＝log5(2x＋1)的单调增区间是________．‎ 答案　 解析　要使y＝log5(2x＋1)有意义，则2x＋1＞0，即x＞－，而y＝log5u为(0，＋∞)上的增函数，当x＞－时，u＝2x＋1也为R上的增函数，故原函数的单调增区间是.‎ ‎1.比较两个对数值的大小及解对数不等式问题，其依据是对数函数的单调性．‎ 若对数的底数是字母且范围不明确，一般要分a＞1和0＜a＜1两类分别求解．‎ ‎2．解决与对数函数相关的问题时要树立“定义域优先”的原则，同时注意数形结合思想和分类讨论思想在解决问题中的应用．‎ 一、基础达标 ‎1．若集合A＝，则∁RA等于(　　)‎ A．(－∞，0]∪ B. C．(－∞，0]∪ D. 答案　A 解析　logx≥，即logx≥log，∴0＜x≤，‎ 即A＝，∴∁RA＝.故选A.‎ ‎2．设a＝log3π，b＝log2，c＝log3，则(　　)‎ A．a＞b＞c B．a＞c＞b C．b＞a＞c D．b＞c＞a 答案　A 解析　a＝log3π＞1，b＝log2＝log23∈，c＝log3＝log32∈，故有a＞b＞c.‎ ‎3．函数f(x)＝logax(0＜a＜1)在[a2，a]上的最大值是(　　)‎ A．0 B．1 C．2 D．a 答案　C 解析　∵0＜a＜1，∴f(x)＝logax在[a2，a]上是减函数，‎ ‎∴f(x)max＝f(a2)＝logaa2＝2.‎ ‎4．函数f(x)＝lg()的奇偶性是(　　)‎ A．奇函数 B．偶函数 C．即奇又偶函数 D．非奇非偶函数 答案　A 解析　f(x)定义域为R，‎ ‎∵f(－x)＋f(x)‎ ‎＝lg()＋lg()‎ ‎＝lg＝lg 1＝0，‎ ‎∴f(x)为奇函数，选A.‎ ‎5．函数y＝log(－x2＋4x＋12)的单调递减区间是(　　)‎ A．(－∞，2) B．(2，＋∞)‎ C．(－2,2) D．(－2,6)‎ 答案　C 解析　y＝logu，u＝－x2＋4x＋12.‎ 令u＝－x2＋4x＋12＞0，得－2＜x＜6.‎ ‎∴x∈(－2,2)时，u＝－x2＋4x＋12为增函数，‎ ‎∵y＝log(－x2＋4x＋12)为减函数，‎ ‎∴函数的单调减区间是(－2,2)．‎ ‎6．已知定义域为R的偶函数f(x)在[0，＋∞)上是增函数，且f()＝0，则不等式f(log4x)＜0的解集是________．‎ 答案　{x|＜x＜2}‎ 解析　由题意可知，f(log4x)＜0⇔－＜log4x＜⇔log44＜log4x＜log44⇔＜x＜2.‎ ‎7．已知f(x)＝(logx)2－3logx，x∈[2,4]．试求f(x)的最大值与最小值．‎ 解　令t＝logx，‎ 则y＝t2－3t＝(t－)2－，‎ ‎∵2≤x≤4，∴log4≤logx≤log2，‎ 即－2≤t≤－1.‎ 可知y＝(t－)2－在[－2，－1]上单调递减．‎ ‎∴当t＝－2时，y取最大值为10；‎ 当t＝－1时，y取最小值为4.‎ 故f(x)的最大值为10，最小值为4.‎ 二、能力提升 ‎8．设a＝log36，b＝log510，c＝log714，则(　　)‎ A．c＞b＞a B．b＞c＞a C．a＞c＞b D．a＞b＞c 答案　D 解析　a＝log36＝log33＋log32＝1＋log32，‎ b＝log510＝log55＋log52＝1＋log52，‎ c＝log714＝log77＋log72＝1＋log72，‎ ‎∵log32＞log52＞log72，∴a＞b＞c，故选D.‎ ‎9．已知函数f(x)是定义在R上的偶函数，且在区间[0，＋∞)上单调递增．若实数a满足f(log2a)＋f(loga)≤2f(1)，则a的取值范围是(　　)‎ A．[1,2] B. C．[，2] D．(0,2]‎ 答案　C 解析　∵f(loga)＝f(－log2a)＝f(log2a)，∴原不等式可化为f(log2a)≤f(1)．又∵f(x)在区间[0，＋∞)上单调递增，∴0≤log2a≤1，即1≤a≤2.∵f(x)是偶函数，∴f(log2a)≤f(－1)．又f(x)在区间(－∞，0]上单调递减，∴－1≤log2a≤0，∴≤a≤1.综上可知≤a≤2.‎ ‎10．已知函数f(x)＝若f(x)在(－∞，＋∞)上单调递增，则实数a的取值范围为________．‎ 答案　{a|2＜a≤3}‎ 解析　∵函数f(x)是(－∞，＋∞)上的增函数，‎ ‎∴a的取值需满足 解得2＜a≤3.‎ ‎11．讨论函数f(x)＝loga(3x2－2x－1)的单调性．‎ 解　由3x2－2x－1＞0得函数的定义域为 .‎ 则当a＞1时，‎ 若x＞1，则u＝3x2－2x－1为增函数，‎ ‎∴f(x)＝loga(3x2－2x－1)为增函数．‎ 若x＜－，则u＝3x2－2x－1为减函数．‎ ‎∴f(x)＝loga(3x2－2x－1)为减函数．‎ 当0＜a＜1时，‎ 若x＞1，则f(x)＝loga(3x2－2x－1)为减函数；‎ 若x＜－，则f(x)＝loga(3x2－2x－1)为增函数．‎ 三、探究与创新 ‎12．已知x满足不等式：2(logx)2＋7logx＋3≤0，求函数f(x)＝·的最大值和最小值．‎ 解　由2(logx)2＋7logx＋3≤0，‎ 可解得－3≤logx≤－，即≤x≤8，‎ ‎∴≤log2x≤3.‎ ‎∵f(x)＝(log2x－2)(log2x－1)‎ ‎＝2－，‎ ‎∴当log2x＝，即x＝2时，f(x)有最小值－.‎ 当log2x＝3，即x＝8时，f(x)有最大值2.‎ ‎∴f(x)min＝－，f(x)max＝2.‎ ‎13．已知f(x)＝2＋log3x，x∈[1,9]，求y＝[f(x)]2＋f(x2)的最大值以及y取最大值时x的值．‎ 解　∵f(x)＝2＋log3x，‎ ‎∴y＝[f(x)]2＋f(x2)‎ ‎＝(2＋log3x)2＋2＋log3x2‎ ‎＝(2＋log3x)2＋2＋2log3x ‎＝(log3x)2＋6log3x＋6‎ ‎＝(log3x＋3)2－3.‎ ‎∵函数f(x)的定义域为[1,9]，‎ ‎∴要使函数y＝[f(x)]2＋f(x2)有意义，‎ 必须满足∴1≤x≤3，‎ ‎∴0≤log3x≤1.∴6≤y＝(log3x＋3)2－3≤13.‎ 当log3x＝1，即x＝3时，y＝13.‎ ‎∴当x＝3时，函数y＝[f(x)]2＋f(x2)取得最大值13.‎