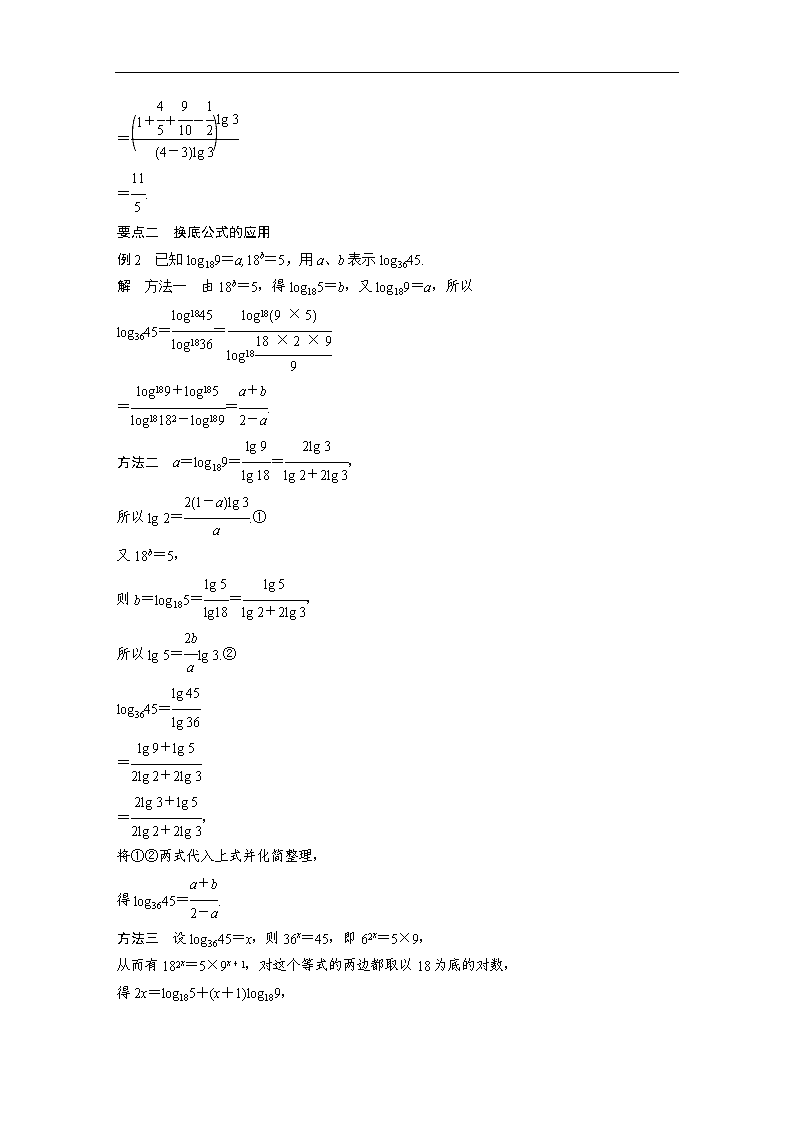高中数学必修1教案第二章 2_2_1 第2课时对数的运算 9页

第2课时　对数的运算 ‎[学习目标]　1.掌握对数的运算性质，能运用运算性质进行对数的有关计算.2.了解换底公式，能用换底公式将一般对数化为自然对数或常用对数．‎ ‎[知识链接]‎ 在指数的运算性质中：‎ am·an＝am＋n，＝am－n，(am)n＝amn.‎ ‎[预习导引]‎ ‎1．对数的运算性质 如果a＞0，且a≠1，M＞0，N＞0.那么：‎ ‎(1)loga(M·N)＝logaM＋logaN.‎ ‎(2)loga＝logaM－logaN.‎ ‎(3)logaMn＝nlogaM，(n∈R)．‎ ‎2．换底公式 logab＝(a＞0，且a≠1；c＞0，且c≠1；b>0)．‎ 温馨提示　常用结论(1)loganbn＝logab；‎ ‎(2)logambn＝logab；‎ ‎(3)logab·logba＝1；‎ ‎(4)logab·logbc·logcd＝logad.‎ 要点一　对数运算性质的应用 例1　计算下列各式的值：‎ ‎(1)lg－lg ＋lg；‎ ‎(2)lg 25＋lg 8＋lg 5×lg 20＋(lg 2)2.‎ 解　(1)方法一　原式＝(5lg 2－2lg 7)－×lg 2＋(2lg 7＋lg 5)‎ ‎＝lg 2－lg 7－2lg 2＋lg 7＋lg 5‎ ‎＝lg 2＋lg 5＝(lg 2＋lg 5)＝lg 10‎ ‎＝.‎ 方法二　原式＝lg－lg 4＋lg 7＝lg ‎＝lg(·)＝lg＝.‎ ‎(2)原式＝2lg 5＋2lg 2＋lg 5(2lg 2＋lg 5)＋(lg 2)2‎ ‎＝2lg 10＋(lg 5＋lg 2)2＝2＋(lg 10)2＝2＋1＝3.‎ 规律方法　1.对于同底的对数的化简，常用方法是(1)“收”，将同底的两对数的和(差)收成积(商)的对数．(2)“拆”，将积(商)的对数拆成对数的和(差)．‎ ‎2．对数式的化简，求值一般是正用或逆用公式．要养成正用、逆用、变形应用公式的习惯，lg 2＋lg 5＝1在计算对数值时会经常用到，同时注意各部分变形要化到最简形式．‎ 跟踪演练1　计算下列各式的值：‎ ‎(1)(lg 5)2＋2lg 2－(lg 2)2；‎ ‎(2).‎ 解　(1)原式＝(lg 5)2＋lg 2(2－lg 2)‎ ‎＝(lg 5)2＋(1＋lg 5)lg 2‎ ‎＝(lg 5)2＋lg 2·lg 5＋lg 2‎ ‎＝(lg 5＋lg 2)·lg 5＋lg 2‎ ‎＝lg 5＋lg 2＝1.‎ ‎(2)原式＝ ‎＝ ‎＝.‎ 要点二　换底公式的应用 ‎ 例2　已知log189＝a,18b＝5，用a、b表示log3645.‎ 解　方法一　由18b＝5，得log185＝b，又log189＝a，所以 log3645＝＝ ‎＝＝.‎ 方法二　a＝log189＝＝，‎ 所以lg 2＝.①‎ 又18b＝5，‎ 则b＝log185＝＝，‎ 所以lg 5＝lg 3.②‎ log3645＝ ‎＝ ‎＝，‎ 将①②两式代入上式并化简整理，‎ 得log3645＝.‎ 方法三　设log3645＝x，则36x＝45，即62x＝5×9，‎ 从而有182x＝5×9x＋1，对这个等式的两边都取以18为底的对数，‎ 得2x＝log185＋(x＋1)log189，‎ 又18b＝5，所以b＝log185.‎ 所以2x＝b＋(x＋1)a，‎ 解得x＝，即log3645＝.‎ 规律方法　1.利用换底公式可以把不同底的对数化为同底的对数，要注意换底公式的正用、逆用以及变形应用．‎ ‎2．题目中有指数式与对数式时，要注意将指数式与对数式进行互化、统一成一种形式．‎ 跟踪演练2　(1)(log29)·(log34)等于(　　)‎ A. B. C．2 D．4‎ ‎(2)log2·log3·log5＝________.‎ 答案　(1)D　(2)－12‎ 解析　(1)(log29)·lg34＝(log232)·(log322)‎ ‎＝2log23·(2log32)＝4log23·log32＝4.‎ ‎(2)原式＝·· ‎＝＝－12.‎ 要点三　对数的实际应用 例3　一种放射性物质不断变化为其他物质，每经过一年剩余的质量约是原来的75%，估计约经过多少年，该物质的剩余量是原来的(结果保留1位有效数字)？(lg 2≈0.301 0，lg 3≈0.477 1)‎ 解　设最初的质量是1，经过x年，剩余量是y，则：‎ 经过1年，剩余量是y＝0.75；‎ 经过2年，剩余量是y＝0.752；‎ ‎……‎ 经过x年，剩余量是y＝0.75x；‎ 由题意得0.75x＝，‎ ‎∴x＝log0.75＝＝≈4.‎ ‎∴估计经过4年，该物质的剩余量是原来的.‎ 规律方法　解决对数应用题的一般步骤 跟踪演练3　里氏震级M的计算公式为：M＝lg A－lg A0，其中A是测震仪记录的地震曲线的最大振幅，A0是相应的标准地震的振幅．假设在一次地震中，测震仪记录的最大振幅是1 000，此时标准地震的振幅为0.001，则此次地震的震级为________级；9级地震的最大振幅是5级地震最大振幅的________倍．‎ 答案　6　10 000‎ 解析　由M＝lg A－lg A0知，M＝lg 1 000－lg 0.001＝6，所以此次地震的级数为6级．设9‎ 级地震的最大振幅为A1,5级地震的最大振幅为A2，则lg＝lg A1－lg A2＝(lg A1－lg A0)－(lg A2－lg A0)＝9－5＝4.所以＝104＝10 000.所以9级地震的最大振幅是5级地震的最大振幅的10 000倍．‎ ‎1．下列式子中成立的是(假定各式均有意义)(　　)‎ A．logax·logay＝loga(x＋y)‎ B．(logax)n＝nlogax C.＝loga D.＝logax－logay 答案　C 解析　根据对数的运算性质知，C正确．‎ ‎2．lg 8＋3lg 5的值为(　　)‎ A．－3 B．－1‎ C．1 D．3‎ 答案　D 解析　lg 8＋3lg 5＝lg 8＋lg 53＝lg 8＋lg 125‎ ‎＝lg (8×125)＝lg 1 000＝3.‎ ‎3．lg＋lg的值是________．‎ 答案　1‎ 解析　lg＋lg＝lg＝lg 10＝1.‎ ‎4.＝________.‎ 答案　2‎ 解析　＝log39＝log332＝2.‎ ‎5．已知2m＝5n＝10，则＋＝________.‎ 答案　1‎ 解析　因为m＝log210，n＝log510，所以＋＝log102＋log105＝lg10＝1.‎ ‎1.换底公式可完成不同底数的对数式之间的转化，可正用，逆用；使用的关键是恰当选择底数，换底的目的是利用对数的运算性质进行对数式的化简．‎ ‎2．运用对数的运算性质应注意：‎ ‎(1)在各对数有意义的前提下才能应用运算性质．‎ ‎(2)根据不同的问题选择公式的正用或逆用．‎ ‎(3)在运算过程中避免出现以下错误：‎ ‎①logaNn＝(logaN)n，②loga(MN)＝logaM·logaN，‎ ‎③logaM±logaN＝loga(M±N)．‎ 一、基础达标 ‎1．log242＋log243＋log244等于(　　)‎ A．1 B．2 C．24 D. 答案　A 解析　log242＋log243＋log244＝log24(2×3×4)＝log2424＝1.‎ ‎2．化简log612－2log6的结果为(　　)‎ A．6 B．12 C．log6 D. 答案　C 解析　原式＝log6－log62＝log6＝log6.‎ ‎3．化简＋log2，得(　　)‎ A．2 B．2－2log23‎ C．－2 D．2log23－2‎ 答案　B 解析　＝＝2－log23.‎ ‎∴原式＝2－log23＋log23－1＝2－2log23.‎ ‎4．计算log916·log881的值为(　　)‎ A．18 B. C. D. 答案　C 解析　log916·log881＝· ‎＝·＝.‎ ‎5．log29·log278＝________.‎ 答案　2‎ 解析　log29·log278＝·＝＝2.‎ ‎6．化简(log43＋log83)(log32＋log92)＝________.‎ 答案　 解析　原式＝(＋)(＋)‎ ‎＝log23·＝.‎ ‎7．计算下列各式的值：‎ ‎(1)；‎ ‎(2)lg 5(lg 8＋lg 1 000)＋(lg 2 )2＋lg ＋lg 0.06.‎ 解　(1)原式＝＝＝1.‎ ‎(2)原式＝lg 5(3lg 2＋3)＋3(lg 2)2－lg 6＋lg 6－2‎ ‎＝3·lg 5·lg 2＋3lg 5＋3lg22－2‎ ‎＝3lg 2(lg 5＋lg 2)＋3lg 5－2＝3lg 2＋3lg 5－2‎ ‎＝3(lg 2＋lg 5)－2＝3－2＝1.‎ 二、能力提升 ‎8．若lg a，lg b是方程2x2－4x＋1＝0的两个根，则(lg )2的值等于(　　)‎ A．2 B. C．4 D. 答案　A 解析　由根与系数的关系，得lg a＋lg b＝2，‎ lg a·lg b＝，‎ ‎∴(lg )2＝(lg a－lg b)2‎ ‎＝(lg a＋lg b)2－4lg a·lg b ‎＝22－4×＝2.‎ ‎9．若lg 2＝a，lg 3＝b，则log512等于________．‎ 答案　 解析　log512＝＝＝.‎ ‎10．2008年5月12日，四川汶川发生里氏8.0级特大地震，给人民的生命财产造成了巨大的损失．里氏地震的等级最早是在1935年由美国加州理工学院的地震学家里特判定的．它与震源中心释放的能量(热能和动能)大小有关．震级M＝lg E－3.2，其中E(焦耳)为以地震波的形式释放出的能量．如果里氏6.0级地震释放的能量相当于1颗美国在二战时投放在广岛的原子弹的能量，那么汶川大地震所释放的能量相当于________颗广岛原子弹．‎ 答案　1000‎ 解析　设里氏8.0级、6.0级地震释放的能量分别为E2、E1，‎ 则8－6＝(lgE2－lgE1)，即lg＝3.‎ ‎∴＝103＝1 000，‎ 即汶川大地震所释放的能量相当于1 000颗广岛原子弹．‎ ‎11．计算：(1)3log72－log79＋2log7()；‎ ‎(2)(lg 2)2＋lg 2·lg 50＋lg 25；‎ ‎(3)loga＋loga＋loga.‎ 解　(1)原式＝log78－log79＋log7 ‎＝log78－log79＋log79－log78＝0.‎ ‎(2)原式＝lg 2(lg 2＋lg 50)＋2lg 5＝lg 2·lg 100＋2lg 5‎ ‎＝2lg 2＋2lg 5＝2(lg 2＋lg 5)＝2lg 10＝2.‎ ‎(3)原式＝＋(－n)＋(－)＝－n.‎ 三、探究与创新 ‎12．(1)求2(lg)2＋lg·lg 5＋的值；‎ ‎(2)若log2[log3(log4x)]＝0，log3[log4(log2y)]＝0，‎ 求x＋y的值．‎ 解　(1)原式＝lg(2lg＋lg 5)＋ ‎＝lg (lg 2＋lg 5)＋1－lg ‎＝lg ＋1－lg ＝1.‎ ‎(2)因为log2[log3(log4x)]＝0，‎ 所以log3(log4x)＝1，所以log4x＝3，‎ 所以x＝43＝64.‎ 又因为log3[log4(log2y)]＝0，‎ 所以log4(log2y)＝1，所以log2y＝4，‎ 所以y＝24＝16，‎ ‎∴x＋y＝80.‎ ‎13．已知x，y，z为正数，3x＝4y＝6z，且2x＝py.‎ ‎(1)求p；‎ ‎(2)求证－＝.‎ ‎(1)解　设3x＝4y＝6z＝k(显然k＞0，且k≠1)，‎ 则x＝log3k，y＝log4k，z＝log6k.‎ 由2x＝py，得2log3k＝plog4k＝p·.‎ ‎∵log3k≠0，∴p＝2log34.‎ ‎(2)证明　－＝－＝logk6－logk3＝logk2，‎ 又＝logk4＝logk2，‎ ‎∴－＝.‎