高中数学人教a版选修4-1学业分层测评9弦切角的性质word版含解析 8页

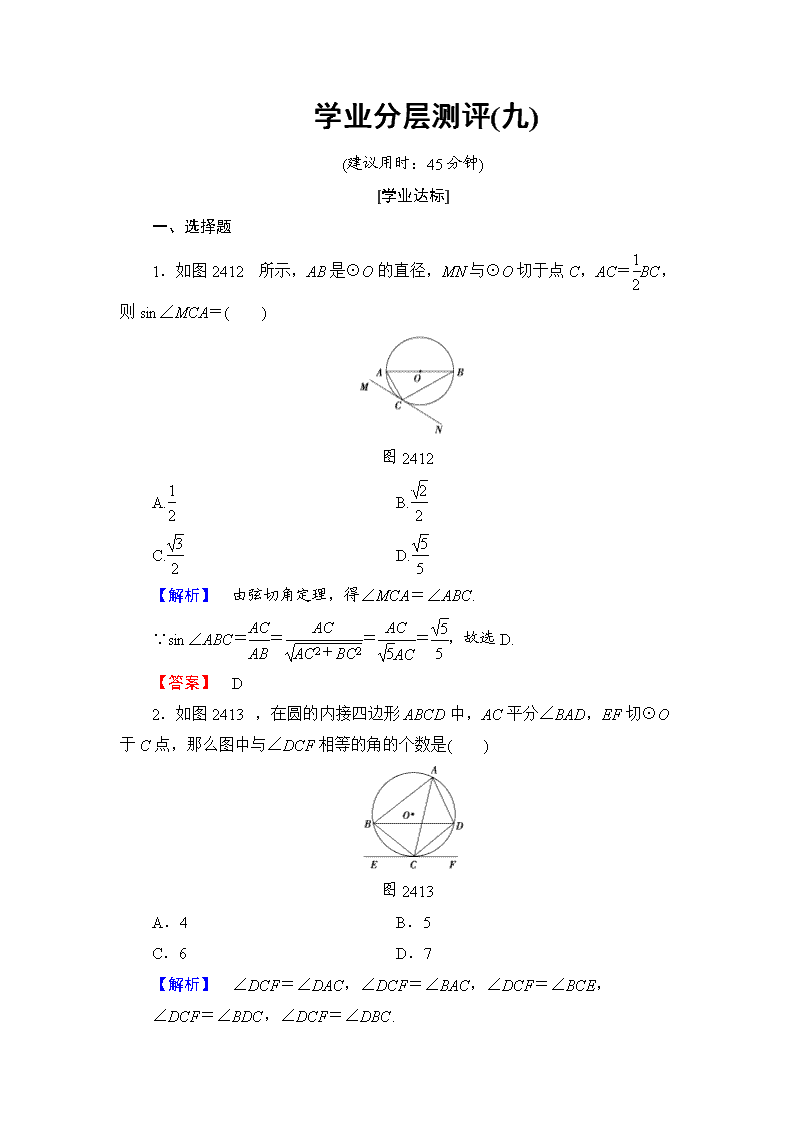
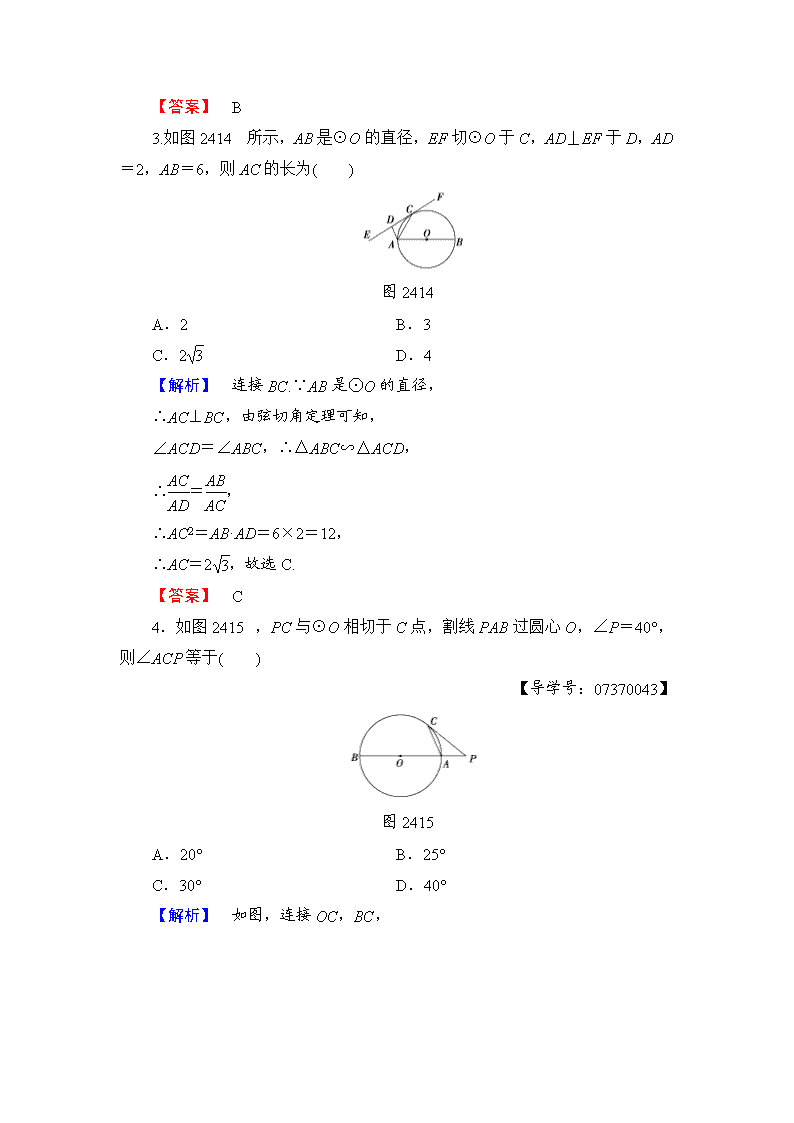
学业分层测评(九) (建议用时：45 分钟) [学业达标] 一、选择题 1．如图 2412 所示，AB 是⊙O 的直径，MN 与⊙O 切于点 C，AC＝1 2BC， 则 sin∠MCA＝( ) 图 2412 A.1 2 B. 2 2 C. 3 2 D. 5 5 【解析】 由弦切角定理，得∠MCA＝∠ABC. ∵sin∠ABC＝AC AB ＝ AC AC2＋BC2 ＝ AC 5AC ＝ 5 5 ，故选 D. 【答案】 D 2．如图 2413，在圆的内接四边形 ABCD 中，AC 平分∠BAD，EF 切⊙O 于 C 点，那么图中与∠DCF 相等的角的个数是( ) 图 2413 A．4 B．5 C．6 D．7 【解析】 ∠DCF＝∠DAC，∠DCF＝∠BAC，∠DCF＝∠BCE， ∠DCF＝∠BDC，∠DCF＝∠DBC. 【答案】 B 3.如图 2414 所示，AB 是⊙O 的直径，EF 切⊙O 于 C，AD⊥EF 于 D，AD ＝2，AB＝6，则 AC 的长为( ) 图 2414 A．2 B．3 C．2 3 D．4 【解析】 连接 BC.∵AB 是⊙O 的直径， ∴AC⊥BC，由弦切角定理可知， ∠ACD＝∠ABC，∴△ABC∽△ACD， ∴AC AD ＝AB AC ， ∴AC2＝AB·AD＝6×2＝12， ∴AC＝2 3，故选 C. 【答案】 C 4．如图 2415，PC 与⊙O 相切于 C 点，割线 PAB 过圆心 O，∠P＝40°， 则∠ACP 等于( ) 【导学号：07370043】 图 2415 A．20° B．25° C．30° D．40° 【解析】 如图，连接 OC，BC， ∵PC 切⊙O 于 C 点， ∴OC⊥PC，∵∠P＝40°，∴∠POC＝50°. ∵OC＝OB， ∴∠B＝1 2 ∠POC＝25°， ∴∠ACP＝∠B＝25°. 【答案】 B 5．如图 2416 所示，已知 AB，AC 与⊙O 相切于 B，C，∠A＝50°，点 P 是⊙O 上异于 B，C 的一动点，则∠BPC 的度数是( ) 图 2416 A．65° B．115° C．65°或 115° D．130°或 50° 【解析】 当点 P 在优弧 上时， 由∠A＝50°，得∠ABC＝∠ACB＝65°. ∵AB 是⊙O 的切线，∴∠ABC＝∠BPC＝65°. 当 P 点在劣弧 上时，∠BPC＝115°. 故选 C. 【答案】 C 二、填空题 6.如图 2417 所示，直线 PB 与圆 O 相切于点 B，D 是弦 AC 上的点，∠PBA ＝∠DBA.若 AD＝m，AC＝n，则 AB＝________. 图 2417 【解析】 ∵PB 切⊙O 于点 B，∴∠PBA＝∠ACB. 又∠PBA＝∠DBA，∴∠DBA＝∠ACB， ∴△ABD∽△ACB. ∴AB AC ＝AD AB ，∴AB2＝AD·AC＝mn， ∴AB＝ mn. 【答案】 mn 7．如图 2418，已知△ABC 内接于圆 O，点 D 在 OC 的延长线上．AD 是 ⊙O 的切线，若∠B＝30°，AC＝2，则 OD 的长为__________． 图 2418 【解析】 连接 OA， 则∠COA＝2∠CBA＝60°， 且由 OC＝OA 知△COA 为正三角形，所以 OA＝2. 又因为 AD 是⊙O 的切线，即 OA⊥AD， 所以 OD＝2OA＝4. 【答案】 4 8.如图 2419，点 P 在圆 O 直径 AB 的延长线上，且 PB＝OB＝2，PC 切圆 O 于 C 点，CD⊥AB 于 D 点，则 CD＝________. 图 2419 【解析】 连接 OC，∵PC 切⊙O 于点 C， ∴OC⊥PC， ∵PB＝OB＝2，OC＝2， ∴PC＝2 3，∵OC·PC＝OP·CD， ∴CD＝2×2 3 4 ＝ 3. 【答案】 3 三、解答题 9．如图 2420 所示，△ABT 内接于⊙O，过点 T 的切线交 AB 的延长线于 点 P，∠APT 的平分线交 BT，AT 于 C，D. 图 2420 求证：△CTD 为等腰三角形． 【证明】 ∵PD 是∠APT 的平分线，∴∠APD＝∠DPT. 又∵PT 是圆的切线，∴∠BTP＝∠A. 又∵∠TDC＝∠A＋∠APD， ∠TCD＝∠BTP＋∠DPT， ∴∠TDC＝∠TCD，∴△CTD 为等腰三角形． 10．如图 2421，AB 是⊙O 的弦，M 是 上任一点，过点 M 的切线与分 别以 A，B 为垂足的直线 AD，BC 交于 D，C 两点，过 M 点作 NM⊥CD 交 AB 于点 N，求证：MN2＝AD·BC. 图 2421 【证明】 连接 AM，MB， 因为 DA⊥AB，MN⊥CD， 所以∠MDA＋∠MNA＝180°. 又因为∠MNA＋∠MNB＝180°， 所以∠MDA＝∠MNB， 又因为 CD 为⊙O 的切线，所以∠1＝∠2， 所以△ADM∽△MNB， 所以AD MN ＝AM BM ，同理MN BC ＝AM BM ， 所以AD MN ＝MN BC ，即有 MN2＝AD·BC. [能力提升] 1．在圆 O 的直径 CB 的延长线上取一点 A，AP 与圆 O 切于点 P，且∠APB ＝30°，AP＝ 3，则 CP＝( ) 【导学号：07370044】 A. 3 B．2 3 C．2 3－1 D．2 3＋1 【解析】 如图，连接 OP，则 OP⊥PA， 又∠APB＝30°， ∴∠POB＝60°， 在 Rt△OPA 中，由 AP＝ 3， 易知，PB＝OP＝1， 在 Rt△PCB 中， 由 PB＝1，∠PBC＝60°，得 PC＝ 3. 【答案】 A 2．如图 2422，AB 是⊙O 直径，P 在 AB 的延长线上，PD 切⊙O 于 C 点， 连接 AC，若 AC＝PC，PB＝1，则⊙O 的半径为( ) 图 2422 A．1 B．2 C．3 D．4 【解析】 连接 BC. ∵AC＝PC，∴∠A＝∠P. ∵∠BCP＝∠A，∴∠BCP＝∠P， ∴BC＝BP＝1. 由△BCP∽△CAP，得 PC2＝PB·PA， 即 AC2＝PB·PA. 而 AC2＝AB2－BC2， 设⊙O 半径为 r， 则 4r2－12＝1·(1＋2r)，解得 r＝1. 【答案】 A 3．如图 2423，过圆 O 外一点 P 分别作圆的切线和割线交圆于 A，B，且 PB＝7，C 是圆上一点使得 BC＝5，∠BAC＝∠APB，则 AB＝__________. 图 2423 【解析】 由 PA 为⊙O 的切线，BA 为弦， 得∠PAB＝∠BCA. 又∠BAC＝∠APB， 于是△APB∽△CAB， 所以PB AB ＝AB BC. 而 PB＝7，BC＝5， 故 AB2＝PB·BC＝7×5＝35，即 AB＝ 35. 【答案】 35 4．如图 2424，AB 为⊙O 的直径，直线 CD 与⊙O 相切于 E，AD 垂直 CD 于 D，BC 垂直 CD 于 C，EF 垂直 AB 于 F，连接 AE，BE. 图 2424 证明： (1)∠FEB＝∠CEB； (2)EF2＝AD·BC. 【证明】 (1)由直线 CD 与⊙O 相切，得∠CEB＝∠EAB. 由 AB 为⊙O 的直径，得 AE⊥EB，从而∠EAB＋∠EBF＝π 2. 又 EF⊥AB，得∠FEB＋∠EBF＝π 2. 从而∠FEB＝∠EAB，故∠FEB＝∠CEB. (2)由 BC⊥CE，EF⊥AB，∠FEB＝∠CEB，BE 是公共边，得 Rt△BCE≌Rt △BFE，所以 BC＝BF. 类似可证 Rt△ADE≌Rt△AFE，得 AD＝AF. 又在 Rt△AEB 中，EF⊥AB，故 EF2＝AF·BF， 所以 EF2＝AD·BC.