2020高中数学 课时分层作业11 等差数列的前n项和 新人教A版必修5 4页

课时分层作业(十一)　等差数列的前n项和 ‎(建议用时：40分钟)‎ ‎[学业达标练]‎ 一、选择题 ‎1．已知等差数列{an}的前n项和为Sn，若‎2a6＝a8＋6，则S7等于(　　)‎ A．49　　　　　　　　　 B．42‎ C．35 D．28‎ B　[‎2a6－a8＝a4＝6，S7＝(a1＋a7)＝‎7a4＝42.]‎ ‎2．已知数列{an}是等差数列，a4＝15，S5＝55，则过点P(3，a3)，Q(4，a4)的直线斜率为(　　)‎ ‎【导学号：91432169】‎ A．4 B. C．－4 D．－ A　[由题S5＝＝＝55.解得a3＝11.‎ ‎∴P(3,11)，Q(4,15)，‎ ‎∴k＝＝4.故选A.]‎ ‎3．在小于100的自然数中，所有被7除余2的数之和为(　　)‎ A．765 B．665‎ C．763 D．663‎ B　[∵a1＝2，d＝7,2＋(n－1)×7<100，‎ ‎∴n<15，∴n＝14，S14＝14×2＋×14×13×7＝665.]‎ ‎4．设Sn是等差数列{an}的前n项和，若＝，则等于(　　)‎ ‎【导学号：91432170】‎ A．1 B．－1‎ C．2 D. A　[＝＝＝＝·＝1.]‎ ‎5．现有200根相同的钢管，把它们堆成正三角形垛，要使剩余的钢管尽可能少，那么剩余钢管的根数为(　　)‎ - 4 -‎ A．9 B．10‎ C．19 D．29‎ B　[钢管排列方式是从上到下各层钢管数组成了一个等差数列，最上面一层钢管数为1，逐层增加1个．‎ ‎∴钢管总数为：1＋2＋3＋…＋n＝.‎ 当n＝19时，S19＝190.当n＝20时，S20＝210>200.∴n＝19时，剩余钢管根数最少， 为10根．]‎ 二、填空题 ‎6．已知{an}是等差数列，a4＋a6＝6，其前5项和S5＝10，则其公差为d＝________.‎ ‎【导学号：91432171】‎ 　[a4＋a6＝a1＋3d＋a1＋5d＝6，①‎ S5＝‎5a1＋×5×(5－1)d＝10，②‎ 由①②联立解得a1＝1，d＝.]‎ ‎7．已知数列{an}中，a1＝1，an＝an－1＋(n≥2)，则数列{an}的前9项和等于________．‎ ‎27　[由a1＝1，an＝an－1＋(n≥2)，可知数列{an}是首项为1，公差为的等差数列，故S9＝‎9a1＋×＝9＋18＝27.]‎ ‎8．已知等差数列{an}的前n项和为Sn，且6S5－5S3＝5，则a4＝________. ‎ ‎【导学号：91432172】‎ 　[设等差数列{an}的首项为a1，公差为d，由6S5－5S3＝5，得3(a1＋3d)＝1，所以a4＝.]‎ 三、解答题 ‎9．等差数列{an}中，a10＝30，a20＝50.‎ ‎(1)求数列的通项公式；‎ ‎(2)若Sn＝242，求n.‎ ‎[解]　(1)设数列{an}的首项为a1，公差为d.‎ 则解得 ‎∴an＝a1＋(n－1)d＝12＋(n－1)×2＝10＋2n.‎ ‎(2)由Sn＝na1＋d以及a1＝12，d＝2，Sn＝242，‎ - 4 -‎ 得方程242＝12n＋×2，即n2＋11n－242＝0，解得n＝11或n＝－22(舍去)．故n＝11.‎ ‎10．已知等差数列{an}的前n项和Sn＝n2－2n，求a2＋a3－a4＋a5＋a6. 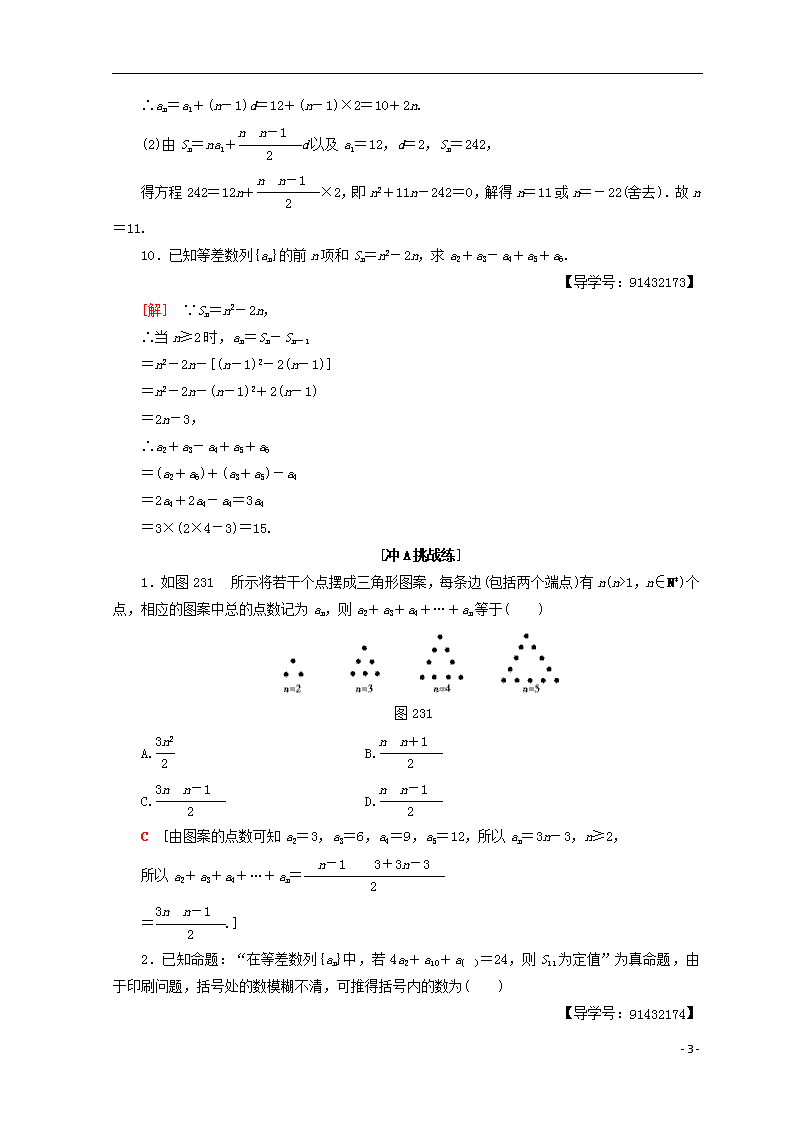‎ ‎【导学号：91432173】‎ ‎[解]　∵Sn＝n2－2n，‎ ‎∴当n≥2时，an＝Sn－Sn－1‎ ‎＝n2－2n－[(n－1)2－2(n－1)]‎ ‎＝n2－2n－(n－1)2＋2(n－1)‎ ‎＝2n－3，‎ ‎∴a2＋a3－a4＋a5＋a6‎ ‎＝(a2＋a6)＋(a3＋a5)－a4‎ ‎＝‎2a4＋‎2a4－a4＝‎3a4‎ ‎＝3×(2×4－3)＝15.‎ ‎[冲A挑战练]‎ ‎1．如图231所示将若干个点摆成三角形图案，每条边(包括两个端点)有n(n>1，n∈N*)个点，相应的图案中总的点数记为an，则a2＋a3＋a4＋…＋an等于(　　)‎ 图231‎ A.　　　　　　 B. C. D. C　[由图案的点数可知a2＝3，a3＝6，a4＝9，a5＝12，所以an＝3n－3，n≥2，‎ 所以a2＋a3＋a4＋…＋an＝ ‎＝.]‎ ‎2．已知命题：“在等差数列{an}中，若‎4a2＋a10＋a(　)＝24，则S11为定值”为真命题，由于印刷问题，括号处的数模糊不清，可推得括号内的数为(　　)‎ ‎【导学号：91432174】‎ A．15 B．24‎ C．18 D．28‎ C　[设括号内的数为n，则‎4a2＋a10＋a(n)＝24，‎ - 4 -‎ ‎∴‎6a1＋(n＋12)d＝24.‎ 又S11＝‎11a1＋55d＝11(a1＋5d)为定值，‎ 所以a1＋5d为定值．‎ 所以＝5，n＝18.]‎ ‎3．设Sn是数列{an}的前n项和，且a1＝－1，an＋1＝SnSn＋1，则Sn＝________.‎ ‎－　[当n＝1时，S1＝a1＝－1，所以＝－1.因为an＋1＝Sn＋1－Sn＝SnSn＋1，所以－＝1，即－＝－1，所以是以－1为首项，－1为公差的等差数列，所以＝(－1)＋(n－1)·(－1)＝－n，所以Sn＝－]‎ ‎4．等差数列{an}的前n项和为Sn，已知am－1＋am＋1－a＝0，S‎2m－1＝38，则m＝________.‎ ‎【导学号：91432175】‎ ‎10　[因为{an}是等差数列， 所以am－1＋am＋1＝2am，由am－1＋am＋1－a＝0，得2am－a＝0，由S‎2m－1＝38知am≠0，所以am＝2，又S‎2m－1＝38，即＝38，即(‎2m－1)×2＝38，解得m＝10.]‎ ‎5．设Sn是数列{an}的前n项和且n∈N*，所有项an>0，且Sn＝a＋an－.‎ ‎(1)证明：{an}是等差数列．‎ ‎(2)求数列{an}的通项公式．‎ ‎[解]　(1)证明：当n＝1时，a1＝S1＝a＋a1－，解得a1＝3或a1＝－1(舍去)．‎ 当n≥2时，‎ an＝Sn－Sn－1＝(a＋2an－3)－(a＋2an－1－3)．‎ 所以4an＝a－a＋2an－2an－1，‎ 即(an＋an－1)(an－an－1－2)＝0，‎ 因为an＋an－1>0，所以an－an－1＝2(n≥2)．所以数列{an}是以3为首项，2为公差的等差数列．‎ ‎(2)由(1)知an＝3＋2(n－1)＝2n＋1.‎ - 4 -‎