2013年高考数学（理科）真题分类汇编B单元 函数与导数 43页

B单元 函数与导数 ‎ B1　函数及其表示　　　　　　　　　　　　　　　　　　　‎ ‎21．B1，B12[2013·江西卷] 已知函数f(x)＝a，a为常数且a>0.‎ ‎(1)证明：函数f(x)的图像关于直线x＝对称；‎ ‎(2)若x0满足f(f(x0))＝x0，但f(x0)≠x0，则称x0为函数f(x)的二阶周期点．如果f(x)有两个二阶周期点x1，x2，试确定a的取值范围；‎ ‎(3)对于(2)中的x1，x2和a，设x3为函数 f(f(x))的最大值点，A(x1，f(f(x1)))，B(x2，f(f(x2)))，C(x3，0)．记△ABC的面积为S(a)，讨论S(a)的单调性．‎ 解：(1)证明：因为f＝a(1－2|x|)，‎ f＝a(1－2|x|)，‎ 有f＝f，‎ 所以函数f(x)的图像关于直线x＝对称．‎ ‎(2)当0时，有 f(f(x))＝ 所以f(f(x))＝x有四个解0，，，，又f(0)＝0，f＝，‎ f≠，f≠，故只有，是f(x)的二阶周期点．‎ 综上所述，所求a的取值范围为a>.‎ ‎(3)由(2)得x1＝，x2＝，‎ 因为x3为函数f(f(x))的最大值点，所以x3＝，或x3＝.‎ 当x3＝时，S(a)＝，求导得：S′(a)＝.‎ 所以当a∈时，S(a)单调递增，当a∈时S(a)单调递减；‎ 当x3＝时，S(a)＝，求导得：S′(a)＝；‎ 因a>，从而有S′(a)＝>0，‎ 所以当a∈时S(a)单调递增．‎ ‎13．B1，B11[2013·江西卷] 设函数f(x)在(0，＋∞)内可导，且f(ex)＝x＋ex，则f′(1)＝________．‎ ‎13．2　[解析] f(ex)＝x＋ex，利用换元法可得f(x)＝ln x＋x，f′(x)＝＋1，所以f′(1)＝2.‎ ‎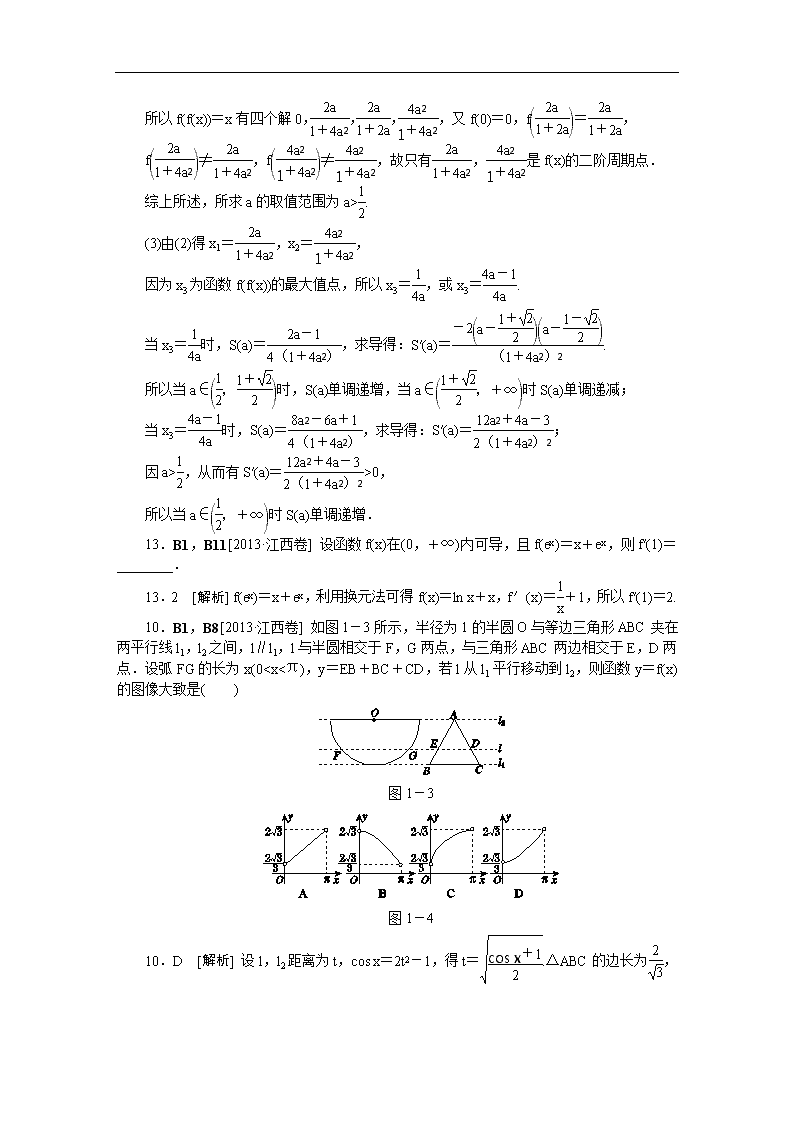10．B1，B8[2013·江西卷] 如图1－3所示，半径为1的半圆O与等边三角形ABC夹在两平行线l1，l2之间，l∥l1，l与半圆相交于F，G两点，与三角形ABC两边相交于E，D两点．设弧FG的长为x(00，得x∈[0，1)，故选B.‎ ‎11．B1[2013·辽宁卷] 已知函数f(x)＝x2－2(a＋2)x＋a2，g(x)＝－x2＋2(a－2)x－a2＋8.设H1(x)＝max，H2(x)＝min(max表示p，q中的较大值，min表示p，q中的较小值)．记H1(x)的最小值为A，H2(x)的最大值为B，则A－B＝(　　)‎ A．16 B．－16‎ C．a2－‎2a－16 D．a2＋‎2a－16‎ ‎11．B　[解析] 由题意知当f(x)＝g(x)时，即x2－2(a＋2)x＋a2＝－x2＋2(a－2)x－a2＋8，‎ 整理得x2－2ax＋a2－4＝0，所以x＝a＋2或x＝a－2，‎ 所以H1(x)＝max{f(x)，g(x)}＝ H2(x)＝min{f(x)，g(x)}＝‎ 由图形(图形略)可知，A＝H1(x)min＝－‎4a－4，B＝H2(x)max＝12－‎4a，则A－B＝－16.‎ 故选B.‎ ‎4．B1[2013·全国卷] 已知函数f(x)的定义域为(－1，0)，则函数f(2x＋1)的定义域为(　　)‎ A．(－1，1) B. C．(－1，0) D. ‎4．B　[解析] 对于f(2x＋1)，－1<2x＋1<0，解得－10时，f[f(x)]表达式的展开式中常数项为(　　)‎ A．－20 B．‎20 C．－15 D．15‎ ‎8．A　[解析] 由已知表达式可得：f[f(x)]＝－6，展开式的通项为Tr＋1＝C6－r(－)r＝C·(－1)r·xr－3，令r－3＝0，可得r＝3，所以常数项为T4＝－C＝－20.‎ ‎7．B1，B3，B12[2013·四川卷] 函数y＝的图像大致是(　　)‎ 图1－5‎ ‎7．C　[解析] 函数的定义域是{x∈R|x≠0}，排除选项A；当x<0时，x3<0，3x－1<0，故y>0，排除选项B；‎ 当x→＋∞时，y>0且y→0，故为选项C中的图像．‎ ‎19．B1，I2，K6[2013·新课标全国卷Ⅱ] 经销商经销某种农产品，在一个销售季度内，每售出1 t该产品获利润500元，未售出的产品，每1 t亏损300元．根据历史资料，得到销售季度内市场需求量的频率分布直方图，如图1－4所示，经销商为下一个销售季度购进了130 t该农产品，以X(单位：t，100≤X≤150)表示下一个销售季度内的市场需求量，T(单位：元)表示下一个销售季度内经销该农产品的利润．‎ ‎(1)将T表示为X的函数；‎ ‎(2)根据直方图估计利润T不少于57 000元的概率；‎ ‎(3)在直方图的需求量分组中，以各组的区间中点值代表该组的各个值，并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如：若需求量X∈[100，110)，则取X＝105，且X＝105的概率等于需求量落入[100，110)的频率)，求T的数学期望．‎ 图1－4‎ ‎19．解：(1)当X∈[100，130)时，‎ T＝500X－300(130－X)＝800X－39 000.‎ 当X∈[130，150]时，T＝500×130＝65 000.‎ 所以T＝ ‎(2)由(1)知利润T不少于57 000元，当且仅当120≤X≤150.‎ 由直方图知需求量X∈[120，150]的频率为0.7，所以下一个销售季度内的利润T不少于57 000元的概率的估计值为0.7.‎ ‎(3)依题意可得T的分布列为 T ‎45 000‎ ‎53 000‎ ‎61 000‎ ‎65 000‎ P ‎0.1‎ ‎0.2‎ ‎0.3‎ ‎0.4‎ 所以E(T)＝45 000×0.1＋53 000×0.2＋61 000×0.3＋65 000×0.4＝59 400.‎ B2　反函数　　　　　　　　　　　　　　　　　　　‎ ‎5．B2[2013·全国卷] 函数f(x)＝log2(x>0)的反函数f－1(x)＝(　　)‎ A.(x>0) B.(x≠0) ‎ C．2x－1(x∈R) D．2x－1(x>0) ‎ ‎5．A　[解析] 令y＝log2，则y>0，且1＋＝2y，解得x＝，交换x，y得f－1(x)＝(x>0)．‎ B3　函数的单调性与最值　　　　　　　　　　　　　　　　　　　‎ ‎21．B3，B9，B12[2013·四川卷] 已知函数f(x)＝其中a是实数．设A(x1，f(x1))，‎ B(x2，f(x2))为该函数图像上的两点，且x10.‎ 因此x2－x1＝[－(2x1＋2)＋2x2＋2]≥＝1，‎ 当且仅当－(2x1＋2)＝2x2＋2＝1，即x1＝－且x2＝－时等号成立．‎ 所以，函数f(x)的图像在点A，B处的切线互相垂直时，x2－x1的最小值为1.‎ ‎(3)当x1x1>0时，f′(x1)≠f′(x2)，故x1<00时，函数f(x)的图像在点(x2，f(x2))处的切线方程为 y－ln x2＝(x－x2)，即y＝·x＋ln x2－1.‎ 两切线重合的充要条件是 由①及x1<0h(0)＝－ln 2－1，‎ 所以a>－ln 2－1.‎ 又当x1∈(－1，0)且趋近于－1时，h(x1)无限增大，‎ 所以a的取值范围是(－ln 2－1，＋∞)．‎ 故当函数f(x)的图像在点A，B处的切线重合时，a的取值范围是(－ln 2－1，＋∞)．‎ ‎10．B3，B12[2013·四川卷] 设函数f(x)＝(a∈R，e为自然对数的底数)．若曲线y＝sinx上存在(x0，y0)使得f(f(y0))＝y0，则a的取值范围是(　　)‎ A．[1，e] B．[e－1－1，1]‎ C．[1，e＋1] D．[e－1－1，e＋1]‎ ‎10．A　[解析] 因为y0＝sin x0∈[－1，1]，且f(x)在[－1，1]上(有意义时)是增函数，对于y0∈[－1，1]，如果f(y0)＝c＞y0，则f(f(y0))＝f(c)＞f(y0)＝c＞y0，不可能有f(f(y0))＝y0.‎ 同理，当f(y0)＝d＜y0时，则f(f(y0))＝f(d)＜f(y0)＝d＜y0，也不可能有f(f(y0))＝y0，因此必有f(y0)＝y0，即方程f(x)＝x在[－1，1]上有解，即＝x在[－1，1]上有解．显然，当x＜0时，方程无解，即需要＝x在[0，1]上有解．当x≥0时，两边平方得ex＋x－a＝x2，故a＝ex－x2＋x.记g(x)＝ex－x2＋x，则g′(x)＝ex－2x＋1.‎ 当x∈时，ex＞0，－2x＋1≥0，故g′(x)＞0，‎ 当x∈时，ex＞＞1，0>－2x＋1≥－1，‎ 故g′(x)＞0.‎ 综上，g′(x)在x∈[0，1]上恒大于0，所以g(x)在[0，1]上为增函数，值域为[1，e]，从而a的取值范围是[1，e]．‎ ‎7．B1，B3，B12[2013·四川卷] 函数y＝的图像大致是(　　)‎ 图1－5‎ ‎7．C　[解析] 函数的定义域是{x∈R|x≠0}，排除选项A；当x<0时，x3<0，3x－1<0，故y>0，排除选项B；‎ 当x→＋∞时，y>0且y→0，故为选项C中的图像．‎ ‎10．B3，B5，B8，B12[2013·新课标全国卷Ⅱ] 已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是(　　)‎ A．x0∈R，f(x0)＝0‎ B．函数y＝f(x)的图像是中心对称图形 C．若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)单调递减 D．若x0是f(x)的极值点，则f′(x0)＝0‎ ‎10．C　[解析] x→－∞ 时，f(x)<0 ，x→＋∞ 时，f(x)>0，f(x) 连续，x0∈R ，f(x0)＝0，A正确；通过平移变换，函数可以化为f(x)＝x3＋c ，从而函数y＝f(x)的图像是中心对称图形，B正确； 若x0是f(x)的极小值点，可能还有极大值点x1 ，则f(x)在区间(x1 ，x0)单调递减．C错误．D正确．故答案为C.‎ B4　函数的奇偶性与周期性　　　　　　　　　　　　　　　　　　　‎ ‎2．B4[2013·广东卷] 定义域为R的四个函数y＝x3，y＝2x，y＝x2＋1，y＝2 sin x中，奇函数的个数是(　　)‎ A．4 B．3 C．2 D．1‎ ‎2．C　[解析] 函数y＝x3，y＝2sin x是奇函数．‎ ‎11．B4[2013·江苏卷] 已知f(x)是定义在R上的奇函数．当x>0时，f(x)＝x2－4x，则不等式f(x)>x的解集用区间表示为________．‎ ‎11．(－5，0)∪(5，＋∞)　[解析] 设x<0，则－x>0.因为f(x)是奇函数，所以f(x)＝－f(－x)＝－(x2＋4x)．‎ 又f(0)＝0，于是不等式f(x)>x等价于 或 解得x>5或－50时，f(x)＝x2＋，则f(－1)＝(　　)‎ A．－2 B．0 C．1 D．2‎ ‎3．A　[解析] ∵f为奇函数，∴f＝－f(1)＝－＝－2.‎ ‎14．B4，E3[2013·四川卷] 已知f(x)是定义域为R的偶函数，当x≥0时，f(x)＝x2－4x，那么，不等式f(x＋2)<5的解集是________．‎ ‎14．(－7，3)　[解析] 当x＋2≥0时，f(x＋2)＝(x＋2)2－4(x＋2)＝x2－4，由f(x＋2)＜5，得x2－4＜5，即x2＜9，解得－3＜x＜3，又x＋2≥0，故－2≤x＜3为所求．又因为f(x)为偶函数，故f(x＋2)的图像关于直线x＝－2对称，于是－7＜x＜－2也满足不等式．‎ ‎(注：本题还可以借助函数的图像及平移变换求解)‎ B5　二次函数　　　　　　　　　　　　　　　　　　　‎ ‎4．A2、B5[2013·安徽卷] “a≤0”是“函数f(x)＝|(ax－1)x|在区间(0，＋∞)内单调递增”‎ 的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎4．C　[解析] f(x)＝|(ax－1)x|＝|ax2－x|，若a＝0，则f(x)＝|x|，此时f(x)在区间(0，＋∞)上单调递增；若a<0，则二次函数y＝ax2－x的对称轴x＝<0，且x＝0时y＝0，此时y＝ax2－x在区间(0，＋∞)上单调递减且y<0恒成立，故f(x)＝|ax2－x|在区间(0，＋∞)上单调递增，故a≤0时，f(x)在区间(0，＋∞)上单调递增，条件是充分的；反之若a>0，则二次函数y＝ax2－x的对称轴x＝>0，且在区间0，上y<0，此时f(x)＝|ax2－x|在区间0，上单调递增，在区间，上单调递减，故函数f(x)不可能在区间(0，＋∞)上单调递增，条件是必要的．‎ ‎5．B5，B9[2013·湖南卷] 函数f(x)＝2ln x的图像与函数g(x)＝x2－4x＋5的图像的交点个数为(　　)‎ A．3 B．2 C．1 D．0‎ ‎5．B　[解析] 法一：作出函数f(x)＝2ln x，g(x)＝x2－4x＋5的图像如图：‎ 可知，其交点个数为2，选B.‎ 法二：也可以采用数值法：‎ x ‎1‎ ‎2‎ ‎4‎ f(x)＝2ln x ‎0‎ ‎2ln 2＝ln 4>1‎ ln 42<5‎ g(x)＝x2－4x＋5‎ ‎2‎ ‎1‎ ‎5‎ 可知它们有2个交点，选B.‎ ‎10．B3，B5，B8，B12[2013·新课标全国卷Ⅱ] 已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是(　　)‎ A．x0∈R，f(x0)＝0‎ B．函数y＝f(x)的图像是中心对称图形 C．若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)单调递减 D．若x0是f(x)的极值点，则f′(x0)＝0‎ ‎10．C　[解析] x→－∞ 时，f(x)<0 ，x→＋∞ 时，f(x)>0，f(x) 连续，x0∈R ，f(x0)＝0，A正确；通过平移变换，函数可以化为f(x)＝x3＋c ，从而函数y＝f(x)的图像是中心对称图形，B正确； 若x0是f(x)的极小值点，可能还有极大值点x1 ，则f(x)在区间(x1 ，x0)单调递减．C错误．D正确．故答案为C.‎ B6　指数与指数函数　　　　　　　　　　　　　　　　　　　‎ ‎6．E3、B6、B7[2013·安徽卷] 已知一元二次不等式f(x)<0的解集为x)x<－1或x>，则f(10x)>0的解集为(　　)‎ A．{x|x<－1或x>－lg 2} ‎ B．{x|－1－lg 2} ‎ D．{x|x<－lg 2}‎ ‎6．D　[解析] 根据已知可得不等式f(x)>0的解是－1a>0，c>b>0.‎ ‎(1)记集合M＝{(a，b，c)|a，b，c不能构成一个三角形的三条边长，且a＝b}，则(a，b，c)∈M所对应的f(x)的零点的取值集合为________；‎ ‎(2)若a，b，c是△ABC的三条边长，则下列结论正确的是________．(写出所有正确结论的序号)‎ ‎①x∈(－∞，1)，f(x)>0；‎ ‎②x∈R，使ax，bx，cx不能构成一个三角形的三条边长；‎ ‎③若△ABC为钝角三角形，则x∈(1，2)，使f(x)＝0.‎ ‎16．(1){x|0a>0，c>b>0，故a＋b＝2aa>0，c>b>0，则0<<1，0<<1，当x∈(－∞，1)时，有>，>，所以＋>＋，又a，b，c为三角形三边，则定有a＋b>c，故对x∈(－∞，1)，＋－1>0，即f(x)＝ax＋bx－cx＝cx>0，故①正确；取x＝2，则＋<＋，取x＝3，则＋<＋，由此递推，必然存在x＝n时，有＋<1，即an＋bn0，f(2)＝a2＋b2－c2<0(C为钝角)，根据零点存在性定理可知，x∈(1，2)，使f(x)＝0，故③正确．故填①②③.‎ ‎3．B6，B7[2013·浙江卷] 已知x，y为正实数，则(　　)‎ A．2lg x＋lg y＝2lg x＋2lg y B．2lg(x＋y)＝2lg x·2lg y C．2lg x·lg y＝2lg x＋2lg y D．2lg(xy)＝2lg x·2lg y ‎3．D　[解析] ∵lg(xy)＝lg x＋lg y，∴2lg(xy)＝2lg x＋lg y＝2lgx2lgy，故选择D.‎ B7　对数与指数函数　　　　　　　　　　　　　　　　　　　‎ ‎6．E3、B6、B7[2013·安徽卷] 已知一元二次不等式f(x)<0的解集为x)x<－1或x>，则f(10x)>0的解集为(　　)‎ A．{x|x<－1或x>－lg 2} ‎ B．{x|－1－lg 2} ‎ D．{x|x<－lg 2}‎ ‎6．D　[解析] 根据已知可得不等式f(x)>0的解是－10，b>0，则ln＋(ab)＝bln＋a；‎ ‎②若a>0，b>0，则ln＋(ab)＝ln＋a＋ln＋b；‎ ‎③若a>0，b>0，则ln＋≥ln＋a－ln＋b；‎ ‎④若a>0，b>0，则ln＋(a＋b)≤ln＋a＋ln＋b＋ln 2.‎ 其中的真命题有________．(写出所有真命题的编号)‎ ‎16．①③④　[解析] ①中，当ab≥1时，∵b>0，∴a≥1，ln＋(ab)＝ln ab＝bln a＝bln＋a；当00，∴01时，左边＝ln＋(ab)＝0，右边＝ln＋a＋ln＋b＝ln a＋0＝ln a>0，∴②不成立；‎ ‎③中，当≤1，即a≤b时，左边＝0，右边＝ln＋a－ln＋b≤0，左边≥右边成立；当>1时，左边＝ln＝ln a－ln b>0，若a>b>1时，右边＝ln a－ln b，左边≥右边成立；若01>b>0，左边＝ln＝ln a－ln b>ln a，右边＝ln a，左边≥右边成立，∴③正确；‎ ‎④中，若00，左边≤右边；若a＋b≥1，ln＋－ln 2＝ln－ln 2＝ln，‎ 又∵≤a或≤b，a，b至少有1个大于1，∴ln≤ln a或ln≤ln b，即有ln＋－ln 2＝ln－ln 2＝ln≤ln＋a＋ln＋b，∴④正确．‎ ‎8．B7，E1[2013·新课标全国卷Ⅱ] 设a＝log36，b＝log510，c＝log714，则(　　)‎ A．c＞b＞a B．b＞c＞a C．a＞c＞b D．a＞b＞c ‎8．D　[解析] a－b＝log36－log510＝(1＋log32)－(1＋log52)＝log32－log52>0，‎ b－c＝log510－log714＝(1＋log52)－(1＋log72)＝log52－log72>0，‎ 所以a>b>c，选D.‎ ‎3．B6，B7[2013·浙江卷] 已知x，y为正实数，则(　　)‎ A．2lg x＋lg y＝2lg x＋2lg y B．2lg(x＋y)＝2lg x·2lg y C．2lg x·lg y＝2lg x＋2lg y D．2lg(xy)＝2lg x·2lg y ‎3．D　[解析] ∵lg(xy)＝lg x＋lg y，∴2lg(xy)＝2lg x＋lg y＝2lgx2lgy，故选择D.‎ B8　幂函数与函数的图像　　　　　　　　　　　　　　　　　　　‎ ‎5．B8[2013·北京卷] 函数f(x)的图像向右平移1个单位长度，所得图像与曲线y＝ex关于y轴对称，则f(x)＝(　　)‎ A．ex＋1 B．ex－1 C．e－x＋1 D．e－x－1‎ ‎5．D　[解析] 依题意，f(x)向右平移一个单位长度得到f(x－1)的图像，又y＝ex的图像关于y轴对称的图像的解析式为y＝e－x，所以f(x－1)＝e－x，所以f(x)＝e－x－1.‎ ‎10．B1，B8[2013·江西卷] 如图1－3所示，半径为1的半圆O与等边三角形ABC夹在两平行线l1，l2之间，l∥l1，l与半圆相交于F，G两点，与三角形ABC两边相交于E，D两点．设弧FG的长为x(00，f(x) 连续，x0∈R ，f(x0)‎ ‎＝0，A正确；通过平移变换，函数可以化为f(x)＝x3＋c ，从而函数y＝f(x)的图像是中心对称图形，B正确； 若x0是f(x)的极小值点，可能还有极大值点x1 ，则f(x)在区间(x1 ，x0)单调递减．C错误．D正确．故答案为C.‎ B9　函数与方程　　　　　　　　　　　　　　　　　　　‎ ‎11．B9，B11[2013·新课标全国卷Ⅰ] 已知函数f(x)＝若|f(x)|≥ax，则a的取值范围是(　　)‎ A．(－∞，0] B．(－∞，1]‎ C．[－2，1] D．[－2，0]‎ ‎11．D　[解析] 方法一：若x≤0，|f(x)|＝|－x2＋2x|＝x2－2x，x＝0时，不等式恒成立，x<0时，不等式可变为a≥x－2，而x－2<－2，可得a≥－2；‎ 若x>0，|f(x)|＝|ln(x＋1)|＝ln(x＋1)，由ln(x＋1)≥ax，可得a≤恒成立，‎ 令h(x)＝，则h′(x)＝，再令g(x)＝－ln(x＋1)，则 g′(x)＝<0，故g(x)在(0，＋∞)上单调递减，所以g(x)0，a≤0.综上可知，－2≤a≤0，故选D.‎ 方法二：数形结合：画出函数|f(x)|＝与直线y＝ax的图像，如下图，要使|f(x)|≥ax恒成立，只要使直线y＝ax的斜率最小时与函数y＝x2－2x，x≤0在原点处的切线斜率相等即可，最大时与x轴的斜率相等即可，‎ 因为y′＝2x－2，所以y′|x＝0＝－2，所以－2≤a≤0.‎ ‎10．B9，B12[2013·安徽卷] 若函数f(x)＝x3＋ax2＋bx＋c有极值点x1，x2，且f(x1)＝x1，则关于x的方程3(f(x))2＋2af(x)＋b＝0的不同实根个数是(　　)‎ A．3 B．4‎ C．5 D．6‎ ‎10．A　[解析] 因为f′(x)＝3x2＋2ax＋b，3(f(x))2＋2af(x)＋b＝0且3x2‎ ‎＋2ax＋b＝0的两根分别为x1，x2，所以f(x)＝x1或f(x)＝x2，‎ 当x1是极大值点时，f(x1)＝x1，x2为极小值点，且x2>x1，如图(1)所示，可知方程f(x)＝x1有两个实根，f(x)＝x2有一个实根，故方程3(f(x))2＋2af(x)＋b＝0共有3个不同实根；‎ 当x1是极小值点时，f(x1)＝x1，x2为极大值点，且x21‎ ln 42<5‎ g(x)＝x2－4x＋5‎ ‎2‎ ‎1‎ ‎5‎ 可知它们有2个交点，选B.‎ ‎21．B9、B12[2013·山东卷] 设函数f(x)＝＋c(e＝2.718 28…是自然对数的底数，c ‎∈R)．‎ ‎(1)求f(x)的单调区间、最大值；‎ ‎(2)讨论关于x的方程|ln x|＝f(x)根的个数．‎ ‎21．解：(1)f′(x)＝(1－2x)e－2x.‎ 由f′(x)＝0，解得x＝，‎ 当x<时，f′(x)>0，f(x)单调递增；‎ 当x>时，f′(x)<0，f(x)单调递减．‎ 所以，函数f(x)的单调递增区间是－∞，，单调递减区间是，＋∞，最大值为f＝e－1＋c.‎ ‎(2)令g(x)＝|lnx|－f(x)＝|lnx|－xe－2x－c，x∈(0，＋∞)．‎ ‎①当x∈(1，＋∞)时，lnx>0，则g(x)＝lnx－xe－2x－c，所以g′(x)＝e－2x＋2x－1.因为2x－1>0，>0，所以g′(x)>0.‎ 因此g(x)在(1，＋∞)上单调递增．‎ ‎②当x∈(0，1)时，lnx<0，则g(x)＝－lnx－xe－2x－c，‎ 所以g′(x)＝e－2x－＋2x－1.‎ 因为e2x∈(1，e2)，e2x>1>x>0，所以－<－1.‎ 又2x－1<1，‎ 所以－＋2x－1<0，即g′(x)<0.‎ 因此g(x)在(0，1)上单调递减．‎ 综合①②可知，当x∈(0，＋∞)时，g(x)≥g(1)＝－e－2－c.‎ 当g(1)＝－e－2－c>0，即c<－e－2时，g(x)没有零点，故关于x的方程|lnx|＝f(x)根的个数为0；‎ 当g(1)＝－e－2－c＝0，即c＝－e－2时，g(x)只有一个零点，故关于x的方程|lnx|＝f(x)根的个数为1；‎ 当g(1)＝－e－2－c<0，即c>－e－2时，‎ ‎(ⅰ)当x∈(1，＋∞)时，由(1)知g(x)＝lnx－xe－2x－c≥lnx－e－1＋c>lnx－1－c，‎ 要使g(x)>0，只需使lnx－1－c>0，即x∈(e1＋c，＋∞)；‎ ‎(ⅱ)当x∈(0，1)时，由(1)知g(x)＝－lnx－xe－2x－c≥－lnx－e－1＋c>－lnx－1－c，要使g(x)>0，只需－lnx－1－c>0，即x∈(0，e－1－c)；‎ 所以c>－e－2时，g(x)有两个零点，‎ 故关于x的方程|lnx|＝f(x)根的个数为2.‎ 综上所述，‎ 当c<－e－2时，关于x的方程|lnx|＝f(x)根的个数为0；‎ 当c＝－e－2时，关于x的方程|lnx|＝f(x)根的个数为1；‎ 当c>－e－2时，关于x的方程|lnx|＝f(x)根的个数为2.‎ ‎21．B3，B9，B12[2013·四川卷] 已知函数f(x)＝其中a是实数．设A(x1，f(x1))，‎ B(x2，f(x2))为该函数图像上的两点，且x10.‎ 因此x2－x1＝[－(2x1＋2)＋2x2＋2]≥＝1，‎ 当且仅当－(2x1＋2)＝2x2＋2＝1，即x1＝－且x2＝－时等号成立．‎ 所以，函数f(x)的图像在点A，B处的切线互相垂直时，x2－x1的最小值为1.‎ ‎(3)当x1x1>0时，f′(x1)≠f′(x2)，故x1<00时，函数f(x)的图像在点(x2，f(x2))处的切线方程为 y－ln x2＝(x－x2)，即y＝·x＋ln x2－1.‎ 两切线重合的充要条件是 由①及x1<0h(0)＝－ln 2－1，‎ 所以a>－ln 2－1.‎ 又当x1∈(－1，0)且趋近于－1时，h(x1)无限增大，‎ 所以a的取值范围是(－ln 2－1，＋∞)．‎ 故当函数f(x)的图像在点A，B处的切线重合时，a的取值范围是(－ln 2－1，＋∞)．‎ ‎7．B9[2013·天津卷] 函数f(x)＝2x|log0.5x|－1的零点个数为(　　)‎ A．1 B．2 C．3 D．4‎ ‎7．B　[解析] f(x)＝2x|log0.5 x|－1＝＝ ‎∵f(x)＝－2xlog2x－1在(0，1]上递减且x接近于0时，f(x)接近于正无穷大，f(1)＝－1<0，∴f(x)在(0，1]上有一零点；又∵f(x)＝2xlog2x－1在(1，＋∞)上递增，且f(2)＝22×log2 2－1＝3>0，∴f(x)在(1，＋∞)上有一零点．故f(x)共有2个零点．‎ B10　函数模型及其应用　　　　　　　　　　　　　　　　　　　‎ ‎10．B10[2013·陕西卷] 设[x]表示不大于x的最大整数，则对任意实数x，y，有(　　)‎ A．[－x]＝－[x] B．[2x]＝2[x]‎ C．[x＋y]≤[x]＋[y] D．[x－y]≤[x]－[y]‎ ‎10．D　[解析] 可取特值x＝3.5，则[－x]＝[－3.5]＝－4，－[x]＝－[3.5]＝－3，故A错．[2x]＝[7]＝7，2[x]＝2[3.5]＝6，故B错．再取y＝3.8，则[x＋y]＝[7.3]＝7，而[3.5]＋[3.8]＝3＋3＝6，故C错．只有D正确．‎ ‎6．B10[2013·重庆卷] 若a＜b＜c，则函数f(x)＝(x－a)(x－b)＋(x－b)(x－c)＋(x－c)(x－a)的两个零点分别位于区间(　　)‎ A．(a，b)和(b，c)内 B．(－∞，a)和(a，b)内 C．(b，c)和(c，＋∞)内 D．(－∞，a)和(c，＋∞)内 ‎6．A　[解析] 因为f(a)＝(a－b)(a－c)＞0，f(b)＝(b－c)(b－a)＜0，f(c)＝(c－a)(c－b)＞0，所以f(a)f(b)＜0，f(b)f(c)＜0，所以函数的两个零点分别在(a，b)和(b，c)内，故选A.‎ B11　导数及其运算　　　　　　　　　　　　　　　　　　　‎ ‎11．B9，B11[2013·新课标全国卷Ⅰ] 已知函数f(x)＝若|f(x)|≥ax，则a的取值范围是(　　)‎ A．(－∞，0] B．(－∞，1]‎ C．[－2，1] D．[－2，0]‎ ‎11．D　[解析] 方法一：若x≤0，|f(x)|＝|－x2＋2x|＝x2－2x，x＝0时，不等式恒成立，x<0时，不等式可变为a≥x－2，而x－2<－2，可得a≥－2；‎ 若x>0，|f(x)|＝|ln(x＋1)|＝ln(x＋1)，由ln(x＋1)≥ax，可得a≤恒成立，‎ 令h(x)＝，则h′(x)＝，再令g(x)＝－ln(x＋1)，则 g′(x)＝<0，故g(x)在(0，＋∞)上单调递减，所以g(x)0，a≤0.综上可知，－2≤a≤0，故选D.‎ 方法二：数形结合：画出函数|f(x)|＝与直线y＝ax的图像，如下图，要使|f(x)|≥ax恒成立，只要使直线y＝ax的斜率最小时与函数y＝x2－2x，x≤0在原点处的切线斜率相等即可，最大时与x轴的斜率相等即可，‎ 因为y′＝2x－2，所以y′|x＝0＝－2，所以－2≤a≤0.‎ ‎10．B11[2013·广东卷] 若曲线y＝kx＋ln x在点(1，k)处的切线平行于x轴，则k＝________．‎ ‎10．－1　[解析] ∵y′＝k＋，∴y′|x＝1＝k＋1＝0，故k＝－1.‎ ‎13．B1，B11[2013·江西卷] 设函数f(x)在(0，＋∞)内可导，且f(ex)＝x＋ex，则f′(1)＝________．‎ ‎13．2　[解析] f(ex)＝x＋ex，利用换元法可得f(x)＝ln x＋x，f′(x)＝＋1，所以f′(1)＝2.‎ ‎18．B11，B12[2013·北京卷] 设L为曲线C：y＝在点(1，0)处的切线．‎ ‎(1)求L的方程；‎ ‎(2)证明：除切点(1，0)之外，曲线C在直线L的下方．‎ ‎18．解：(1)设f(x)＝，则f′(x)＝.‎ 所以f′(1)＝1.‎ 所以L的方程为y＝x－1.‎ ‎(2)令g(x)＝x－1－f(x)，则除切点之外，曲线C在直线L的下方等价于 g(x)>0(x>0，x≠1)．‎ g(x)满足g(1)＝0，且 g′(x)＝1－f′(x)＝.‎ 当01时，x2－1>0，ln x>0，所以g′(x)>0，‎ 故g(x)单调递增．‎ 所以g(x)>g(1)＝0(x>0，x≠1)．‎ 所以除切点之外，曲线C在直线L的下方．‎ ‎9．B11、B12[2013·全国卷] 若函数f(x)＝x2＋ax＋在是增函数，则a的取值范围是(　　)‎ A．[－1，0] B．[－1，＋∞)‎ C．[0，3] D．[3，＋∞)‎ ‎9．D　[解析] f′(x)＝2x＋a－≥0在上恒成立，即a≥－2x在上恒成立，由于y＝－2x在上单调递减，所以y<3，故只要a≥3.‎ ‎17．B11，B12[2013·重庆卷] 设f(x)＝a(x－5)2＋6ln x，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线与y轴相交于点(0，6)．‎ ‎(1)确定a的值；‎ ‎(2)求函数f(x)的单调区间与极值．‎ ‎17．解：(1)因f(x)＝a(x－5)2＋6ln x，‎ 故f′(x)＝2a(x－5)＋.‎ 令x＝1，得f(1)＝16a，f′(1)＝6－8a，‎ 所以曲线y＝f(x)在点(1，f(1))处的切线方程为y－16a＝(6－8a)(x－1)，‎ 由点(0，6)在切线上可得6－16a＝8a－6，‎ 故a＝.‎ ‎(2)由(1)知，f(x)＝(x－5)2＋6ln x(x＞0)，‎ f′(x)＝x－5＋＝，‎ 令f′(x)＝0，解得x1＝2，x2＝3.‎ 当0＜x＜2或x＞3时，f′(x)＞0，故f(x)在(0，2)，(3，＋∞)上为增函数；当2＜x＜3时，f′(x)＜0，故f(x)在(2，3)上为减函数．‎ 由此可知，f(x)在x＝2处取得极大值f(2)＝＋6ln 2，在x＝3处取得极小值f(3)＝2＋6ln 3.‎ B12　导数的应用　　　　　　　　　　　　　　　　　　　‎ ‎20．B12 、D5[2013·安徽卷] 设函数fn(x)＝－1＋x＋＋＋…＋(x∈R，n∈N*)．证明：‎ ‎(1)对每个n∈N*，存在唯一的xn∈，1，满足fn(xn)＝0；‎ ‎(2)对任意p∈N*，由(1)中xn构成的数列{xn}满足00时，f′n(x)＝1＋＋…＋>0，故fn(x)在(0，＋∞)内单调递增．‎ 由于f1(1)＝0，当n≥2时，fn(1)＝＋＋…＋>0.故fn(1)≥0.又fn＝－1＋＋≤－＋k ‎＝－＋·＝－·n－1<0.‎ 所以存在唯一的xn∈，1，满足fn(xn)＝0.‎ ‎(2)当x>0时，fn＋1(x)＝fn(x)＋≥fn(x)，故fn＋1(xn)>fn(xn)＝fn＋1(xn＋1)＝0.‎ 由fn＋1(x)在(0，＋∞)内单调递增，xn＋10，区间I＝{x|f(x)>0}．‎ ‎(1)求I的长度(注：区间(α，β)的长度定义为β－α)；‎ ‎(2)给定常数k∈(0，1)，当1－k≤a≤1＋k时，求I长度的最小值．‎ ‎17．解：(1)因为方程ax－(1＋a2)x2＝0(a>0)有两个实根x1＝0，x2＝，‎ 故f(x)>0的解集为{x|x10，d(a)单调递增；‎ 当1x1，如图(1)所示，可知方程f(x)＝x1有两个实根，f(x)＝x2有一个实根，故方程3(f(x))2＋2af(x)＋b＝0共有3个不同实根；‎ 当x1是极小值点时，f(x1)＝x1，x2为极大值点，且x20)，‎ 因而f(1)＝1，f′(1)＝－1，‎ 所以曲线y＝f(x)在点A(1，f(1))处的切线方程为y－1＝－(x－1)，‎ 即x＋y－2＝0.‎ ‎(2)由f′(x)＝1－＝，x>0知：‎ ‎①当a≤0时，f′(x)>0，函数f(x)为(0，＋∞)上的增函数，函数f(x)无极值；‎ ‎②当a>0时，由f′(x)＝0，解得x＝a.‎ 又当x∈(0，a)时，f′(x)<0；当x∈(a，＋∞)时，f′(x)>0，从而函数f(x)在x＝a处取得极小值，且极小值为f(a)＝a－aln a，无极大值．‎ 综上，当a≤0时，函数f(x)无极值；‎ 当a>0时，函数f(x)在x＝a处取得极小值a－aln a，无极大值．‎ ‎22．B12，E8[2013·湖北卷] 设n是正整数，r为正有理数．‎ ‎(1)求函数f(x)＝(1＋x)r＋1－(r＋1)x－1(x>－1)的最小值；‎ ‎(2)证明：0时，f′(x)>0，所以f(x)在(0，＋∞)内是增函数，故函数f(x)在x＝0处取得最小值f(0)＝0.‎ ‎(2)由(1)，当x∈(－1，＋∞)时，有f(x)≥f(0)＝0，即(1＋x)r＋1≥1＋(r＋1)x，且等号当且仅当x＝0时成立，故当x>－1且x≠0时，有(1＋x)r＋1>1＋(r＋1)x.①‎ 在①中，令x＝(这时x>－1且x≠0)，得>1＋.‎ 上式两边同乘nr＋1，得(n＋1)r＋1>nr＋1＋nr(r＋1)，即 nr<.②‎ 当n>1时，在①中令x＝－(这时x>－1且x≠0)，类似可得nr>，③‎ 且当n＝1时，③也成立，综合②，③得 0，f(x2)>－ B．f(x1)<0，f(x2)<－ C．f(x1)>0，f(x2)<－ D．f(x1)<0，f(x2)>－ ‎10．D　[解析] f′(x)＝ln x－(2ax－1)＝0ln x＝2ax－1，函数y＝ln x与函数y＝2ax－1的图像有两个交点，令y1＝ln x，y2＝2ax－1，在同一坐标系中作出这两个函数的图像，显然a≤0时，两个函数图像只有一个公共点，故a>0，此时当直线的斜率逐渐变大直到直线y＝2ax－1与曲线y＝ln x相切时，两函数图像均有两个不同的公共点，y′1＝，故曲线y＝ln x上的点(x0，ln x0)处的切线方程是y－ln x0＝(x－x0)，该直线过点(0，－1)，则－1－ln x0＝－1，解得x0＝1，故过点(0，－1)的曲线y＝ln x的切线斜率是1，故2a＝1，即a＝，所以a的取值范围是0，.因为00，f(x)递增，f(1)＝－a，f(x1)f(1)＝－a>－，选D.‎ ‎21．B1，B12[2013·江西卷] 已知函数f(x)＝a，a为常数且a>0.‎ ‎(1)证明：函数f(x)的图像关于直线x＝对称；‎ ‎(2)若x0满足f(f(x0))＝x0，但f(x0)≠x0，则称x0为函数f(x)的二阶周期点．如果f(x)有两个二阶周期点x1，x2，试确定a的取值范围；‎ ‎(3)对于(2)中的x1，x2和a，设x3为函数 f(f(x))的最大值点，A(x1，f(f(x1)))，B(x2，f(f(x2)))，C(x3，0)．记△ABC的面积为S(a)，讨论S(a)的单调性．‎ 解：(1)证明：因为f＝a(1－2|x|)，‎ f＝a(1－2|x|)，‎ 有f＝f，‎ 所以函数f(x)的图像关于直线x＝对称．‎ ‎(2)当0时，有 f(f(x))＝ 所以f(f(x))＝x有四个解0，，，，又f(0)＝0，f＝，‎ f≠，f≠，故只有，是f(x)的二阶周期点．‎ 综上所述，所求a的取值范围为a>.‎ ‎(3)由(2)得x1＝，x2＝，‎ 因为x3为函数f(f(x))的最大值点，所以x3＝，或x3＝.‎ 当x3＝时，S(a)＝，求导得：S′(a)＝.‎ 所以当a∈时，S(a)单调递增，当a∈时S(a)单调递减；‎ 当x3＝时，S(a)＝，求导得：S′(a)＝；‎ 因a>，从而有S′(a)＝>0，‎ 所以当a∈时S(a)单调递增．‎ ‎18．B11，B12[2013·北京卷] 设L为曲线C：y＝在点(1，0)处的切线．‎ ‎(1)求L的方程；‎ ‎(2)证明：除切点(1，0)之外，曲线C在直线L的下方．‎ ‎18．解：(1)设f(x)＝，则f′(x)＝.‎ 所以f′(1)＝1.‎ 所以L的方程为y＝x－1.‎ ‎(2)令g(x)＝x－1－f(x)，则除切点之外，曲线C在直线L的下方等价于 g(x)>0(x>0，x≠1)．‎ g(x)满足g(1)＝0，且 g′(x)＝1－f′(x)＝.‎ 当01时，x2－1>0，ln x>0，所以g′(x)>0，‎ 故g(x)单调递增．‎ 所以g(x)>g(1)＝0(x>0，x≠1)．‎ 所以除切点之外，曲线C在直线L的下方．‎ ‎21．B12[2013·辽宁卷] 已知函数f(x)＝(1＋x)e－2x，g(x)＝ax＋＋1＋2xcos x．当x∈[0，1]时，‎ ‎(1)求证：1－x≤f(x)≤；‎ ‎(2)若f(x)≥g(x)恒成立，求实数a的取值范围．‎ ‎21．解：(1)证明：要证x∈[0，1]时，(1＋x)e－2x≥1－x，只需证明(1＋x)e－x≥(1－x)ex.‎ 记h(x)＝(1＋x)e－x－(1－x)ex，则h′(x)＝x(ex－e－x)，当x∈(0，1)时，h′(x)＞0，因此h(x)在[0，1]上是增函数，故h(x)≥h(0)＝0.‎ 所以f(x)≥1－x，x∈[0，1]．‎ 要证x∈[0，1]时，(1＋x)e－2x≤，只需证明ex≥x＋1.‎ 记K(x)＝ex－x－1，则K′(x)＝ex－1，当x∈(0，1)时，K′(x)＞0，因此K(x)在[0，1]上是增函数，故K(x)≥K(0)＝0.‎ 所以f(x)≤，x∈[0，1]．‎ 综上，1－x≤f(x)≤，x∈[0，1]．‎ ‎(2)(方法一)‎ f(x)－g(x)＝(1＋x)e－2x－ ‎≥1－x－ax－1－－2xcos x ‎＝－x.‎ 设G(x)＝＋2cos x，则G′(x)＝x－2sin x.‎ 记H(x)＝x－2sin x，则H′(x)＝1－2cos x，当x∈(0，1)时，H′(x)＜0，于是G′(x)在[0，1]上是减函数，从而当x∈(0，1)时，G′(x)＜G′(0)＝0，故G(x)在[0，1]上是减函数．于是G(x)≤G(0)＝2.从而 a＋1＋G(x)≤a＋3，‎ 所以，当a≤－3时，f(x)≥g(x)在[0，1]上恒成立．‎ 下面证明，当a＞－3时，f(x)≥g(x)在[0，1]上不恒成立．‎ f(x)－g(x)≤－1－ax－－2xcos x ‎＝－ax－－2xcos x ‎＝－x.‎ 记I(x)＝＋a＋＋2cos x＝＋a＋G(x)，则I′(x)＝＋G′(x)．当x∈(0，1)时，I′(x)＜0.故I(x)在[0，1]上是减函数，于是I(x)在[0，1]上的值域为[a＋1＋2cos 1，a＋3]．‎ 因为当a＞－3时，a＋3＞0，所以存在x0∈(0，1)，使得I(x0)＞0，此时f(x0)＜g(x0)，即f(x)≥g(x)在[0，1]上不恒成立．‎ 综上，实数a的取值范围是(－∞，－3]．‎ ‎(方法二)‎ 先证当x∈[0，1]时，1－x2≤cos x≤1－x2.‎ 记F(x)＝cos x－1＋x2，则F′(x)＝－sin x＋x.‎ 记G(x)＝－sin x＋x，则G′(x)＝－cos x＋1，当x∈(0，1)时，G′(x)＞0，于是G(x)在[0，1]上是增函数，因此当x∈(0，1)时，G(x)＞G(0)＝0，从而F(x)在[0，1]上是增函数，因此F(x)≥F(0)＝0.所以 当x∈[0，1]时，1－x2≤cos x.‎ 同理可证，当x∈[0，1]时，cos x≤1－x2.‎ 综上，当x∈[0，1]时，1－x2≤cos x≤1－x2.‎ 因为当x∈[0，1]时．‎ f(x)－g(x)＝(1＋x)e－2x－ ‎≥(1－x)－ax－－1－2x ‎＝－(a＋3)x.‎ 所以当a≤－3时，f(x)≥g(x)在[0，1]上恒成立．‎ 下面证明，当a＞－3时，f(x)≥g(x)在[0，1]上不恒成立．因为 f(x)－g(x)＝(1＋x)e－2x－ ‎≤－1－ax－－2x ‎＝＋－(a＋3)x ‎≤x，‎ 所以存在x0∈(0，1)例如x0取和中的较小值满足f(x0)＜g(x0)，即f(x)≥g(x)在[0，1]上不恒成立．‎ 综上，实数a的取值范围是(－∞，－3]．‎ ‎12．B12[2013·辽宁卷] 设函数f(x)满足x2f′(x)＋2xf(x)＝，f(2)＝，则x>0时，f(x)(　　)‎ A．有极大值，无极小值 B．有极小值，无极大值 C．既有极大值又有极小值 D．既无极大值也无极小值 ‎12．D　[解析] 因为函数f(x)满足x2f′(x)＋2xf(x)＝[x2·f(x)]′＝，所以当x>0时，′＝>0，令函数g(x)＝x2·f(x)，所以g(x)在x>0时递增．‎ 由f(2)＝，得g(2)＝.‎ 又f(x)＝，‎ 所以f′(x)＝ ‎＝ ‎＝，x>0.‎ 令h(x)＝ex－2g(x)，则h′(x)＝ex，故当x∈(0，2)时，h′(x) <0；当x∈(2，＋∞)时，h′(x)>0，‎ 故h(x)在(0，＋∞)上的最小值为h(2)＝e2－2g(2)＝0.‎ 所以f′(x)＝≥0，故f(x)在(0，∞)单调递增．‎ 所以当x∈(0，＋∞)时，f(x)即无极大值也无极小值．选D.‎ ‎22．B12[2013·全国卷] 已知函数f(x)＝ln(1＋x)－.‎ ‎(1)若x≥0时f(x)≤0，求λ的最小值；‎ ‎(2)设数列{an}的通项an＝1＋＋＋…＋，证明：a2n－an＋＞ln 2.‎ ‎22．解：(1)由已知f(0)＝0，f′(x)＝，f′(0)＝0.‎ 若λ＜，则当0＜x＜2(1－2λ)时，f′(x)＞0，所以f(x)＞0.‎ 若λ≥，则当x＞0时，f′(x)＜0，所以当x＞0时，f(x)＜0.‎ 综上，λ的最小值是.‎ ‎(2)令λ＝.由(1)知，当x＞0时，f(x)＜0，‎ 即＞ln (1＋x)．‎ 取x＝，则＞ln.‎ 于是a2n－an＋＝ ‎＝ ‎＞ln ‎＝ln 2n－ln n ‎＝ln 2.‎ 所以a2n－an＋＞ln 2.‎ ‎9．B11、B12[2013·全国卷] 若函数f(x)＝x2＋ax＋在是增函数，则a的取值范围是(　　)‎ A．[－1，0] B．[－1，＋∞)‎ C．[0，3] D．[3，＋∞)‎ ‎9．D　[解析] f′(x)＝2x＋a－≥0在上恒成立，即a≥－2x在上恒成立，由于y＝－2x在上单调递减，所以y<3，故只要a≥3.‎ ‎21．B9、B12[2013·山东卷] 设函数f(x)＝＋c(e＝2.718 28…是自然对数的底数，c∈R)．‎ ‎(1)求f(x)的单调区间、最大值；‎ ‎(2)讨论关于x的方程|ln x|＝f(x)根的个数．‎ ‎21．解：(1)f′(x)＝(1－2x)e－2x.‎ 由f′(x)＝0，解得x＝，‎ 当x<时，f′(x)>0，f(x)单调递增；‎ 当x>时，f′(x)<0，f(x)单调递减．‎ 所以，函数f(x)的单调递增区间是－∞，，单调递减区间是，＋∞，最大值为f＝e－1＋c.‎ ‎(2)令g(x)＝|lnx|－f(x)＝|lnx|－xe－2x－c，x∈(0，＋∞)．‎ ‎①当x∈(1，＋∞)时，lnx>0，则g(x)＝lnx－xe－2x－c，所以g′(x)＝e－2x＋2x－1.因为2x－1>0，>0，所以g′(x)>0.‎ 因此g(x)在(1，＋∞)上单调递增．‎ ‎②当x∈(0，1)时，lnx<0，则g(x)＝－lnx－xe－2x－c，‎ 所以g′(x)＝e－2x－＋2x－1.‎ 因为e2x∈(1，e2)，e2x>1>x>0，所以－<－1.‎ 又2x－1<1，‎ 所以－＋2x－1<0，即g′(x)<0.‎ 因此g(x)在(0，1)上单调递减．‎ 综合①②可知，当x∈(0，＋∞)时，g(x)≥g(1)＝－e－2－c.‎ 当g(1)＝－e－2－c>0，即c<－e－2时，g(x)没有零点，故关于x的方程|lnx|＝f(x)根的个数为0；‎ 当g(1)＝－e－2－c＝0，即c＝－e－2时，g(x)只有一个零点，故关于x的方程|lnx|＝f(x)根的个数为1；‎ 当g(1)＝－e－2－c<0，即c>－e－2时，‎ ‎(ⅰ)当x∈(1，＋∞)时，由(1)知g(x)＝lnx－xe－2x－c≥lnx－e－1＋c>lnx－1－c，‎ 要使g(x)>0，只需使lnx－1－c>0，即x∈(e1＋c，＋∞)；‎ ‎(ⅱ)当x∈(0，1)时，由(1)知g(x)＝－lnx－xe－2x－c≥－lnx－e－1＋c>－lnx－1－c，要使g(x)>0，只需－lnx－1－c>0，即x∈(0，e－1－c)；‎ 所以c>－e－2时，g(x)有两个零点，‎ 故关于x的方程|lnx|＝f(x)根的个数为2.‎ 综上所述，‎ 当c<－e－2时，关于x的方程|lnx|＝f(x)根的个数为0；‎ 当c＝－e－2时，关于x的方程|lnx|＝f(x)根的个数为1；‎ 当c>－e－2时，关于x的方程|lnx|＝f(x)根的个数为2.‎ ‎21．B12[2013·陕西卷] 已知函数f(x)＝ex，x∈R.‎ ‎(1)若直线y＝kx＋1与f(x)的反函数的图像相切，求实数k的值；‎ ‎(2)设x>0，讨论曲线y＝f(x)与曲线y＝mx2(m>0)公共点的个数；‎ ‎(3)设a0，φ(x)在(2，＋∞)上单调递增，‎ ‎∴φ(x)在(0，＋∞)上的最小值为φ(2)＝.‎ 当0时，在区间(0，2)内存在x1＝，使得φ(x1)>m，在(2，＋∞)内存在x2＝me2，使得φ(x2)>m，由φ(x)的单调性知，曲线y＝与y＝m恰有两个公共点．‎ 综上所述，x>0时，‎ 若0，曲线y＝f(x)与y＝mx2有两个公共点．‎ ‎(3)方法一：‎ 可以证明>.事实上，‎ >>>>1－ >1－(b>a)．(*)‎ 令φ(x)＝＋－1(x≥0)，‎ 则φ′(x)＝－ ‎＝＝≥0(仅当x＝0时等号成立)．‎ ‎∴φ(x)在[0，＋∞)上单调递增，‎ ‎∴x>0时，φ(x)>φ(0)＝0.‎ 令x＝b－a，即得(*)式，结论得证．‎ 方法二：‎ － ‎＝－ ‎＝ ‎＝[(b－a)eb－a＋(b－a)－2eb－a＋2]．‎ 设函数u(x)＝xex＋x－2ex＋2(x≥0)，‎ 则u′(x)＝ex＋xex＋1－2ex，‎ 令h(x)＝u′(x)，则h′(x)＝ex＋ex＋xex－2ex＝xex≥0(仅当x＝0时等号成立)，‎ ‎∴u′(x)单调递增，‎ ‎∴当x>0时，u′(x)>u′(0)＝0，∴u(x)单调递增．‎ 当x>0时，u(x)>u(0)＝0.‎ 令x＝b－a，则得(b－a)eb－a＋(b－a)－2eb－a＋2>0，‎ ‎∴－>0，‎ 因此，>.‎ ‎21．B3，B9，B12[2013·四川卷] 已知函数f(x)＝其中a是实数．设A(x1，f(x1))，‎ B(x2，f(x2))为该函数图像上的两点，且x10.‎ 因此x2－x1＝[－(2x1＋2)＋2x2＋2]≥＝1，‎ 当且仅当－(2x1＋2)＝2x2＋2＝1，即x1＝－且x2＝－时等号成立．‎ 所以，函数f(x)的图像在点A，B处的切线互相垂直时，x2－x1的最小值为1.‎ ‎(3)当x1x1>0时，f′(x1)≠f′(x2)，故x1<00时，函数f(x)的图像在点(x2，f(x2))处的切线方程为 y－ln x2＝(x－x2)，即y＝·x＋ln x2－1.‎ 两切线重合的充要条件是 由①及x1<0h(0)＝－ln 2－1，‎ 所以a>－ln 2－1.‎ 又当x1∈(－1，0)且趋近于－1时，h(x1)无限增大，‎ 所以a的取值范围是(－ln 2－1，＋∞)．‎ 故当函数f(x)的图像在点A，B处的切线重合时，a的取值范围是(－ln 2－1，＋∞)．‎ ‎10．B3，B12[2013·四川卷] 设函数f(x)＝(a∈R，e为自然对数的底数)．若曲线y＝sinx上存在(x0，y0)使得f(f(y0))＝y0，则a的取值范围是(　　)‎ A．[1，e] B．[e－1－1，1]‎ C．[1，e＋1] D．[e－1－1，e＋1]‎ ‎10．A　[解析] 因为y0＝sin x0∈[－1，1]，且f(x)在[－1，1]上(有意义时)是增函数，对于y0∈[－1，1]，如果f(y0)＝c＞y0，则f(f(y0))＝f(c)＞f(y0)＝c＞y0，不可能有f(f(y0))＝y0.‎ 同理，当f(y0)＝d＜y0时，则f(f(y0))＝f(d)＜f(y0)＝d＜y0，也不可能有f(f(y0))＝y0，因此必有f(y0)＝y0，即方程f(x)＝x在[－1，1]上有解，即＝x在[－1，1]上有解．显然，当x＜0时，方程无解，即需要＝x在[0，1]上有解．当x≥0时，两边平方得ex＋x－a＝x2，故a＝ex－x2＋x.记g(x)＝ex－x2＋x，则g′(x)＝ex－2x＋1.‎ 当x∈时，ex＞0，－2x＋1≥0，故g′(x)＞0，‎ 当x∈时，ex＞＞1，0>－2x＋1≥－1，‎ 故g′(x)＞0.‎ 综上，g′(x)在x∈[0，1]上恒大于0，所以g(x)在[0，1]上为增函数，值域为[1，e]，从而a的取值范围是[1，e]．‎ ‎7．B1，B3，B12[2013·四川卷] 函数y＝的图像大致是(　　)‎ 图1－5‎ ‎7．C　[解析] 函数的定义域是{x∈R|x≠0}，排除选项A；当x<0时，x3<0，3x－1<0，故y>0，排除选项B；‎ 当x→＋∞时，y>0且y→0，故为选项C中的图像．‎ ‎20．B12[2013·天津卷] 已知函数f(x)＝x2ln x.‎ ‎(1)求函数f(x)的单调区间；‎ ‎(2)证明：对任意的t>0，存在唯一的s，使t＝f(s)；‎ ‎(3)设(2)中所确定的s关于t的函数为s＝g(t)．证明：当t>e2时，有<<.‎ ‎20．解：(1)函数f(x)的定义域为(0，＋∞)．‎ f′(x)＝2xln x＋x＝x(2ln x＋1)，令f′(x)＝0，得x＝.‎ 当x变化时，f′(x)，f(x)的变化情况如下表：‎ x ‎0， ，＋∞‎ f′(x)‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎  极小值  所以函数f(x)的单调递减区间是0，，单调递增区间是，＋∞.‎ ‎(2)证明：当00，‎ 令h(x)＝f(x)－t，x∈[1，＋∞)．‎ 由(1)知，h(x)在区间(1，＋∞)内单调递增．h(1)＝－t<0，h(et)＝e2tln et－t＝t(e2t－1)>0.故存在唯一的s∈(1，＋∞)，使得t＝f(s)成立．‎ ‎(3)证明：因为s＝g(t)，由(2)知，t＝f(s)，且s>1，从而＝＝＝＝，‎ 其中u＝ln s.‎ 要使<<成立，只需0e2时，若s＝g(t)≤e，则由f(s)的单调性，有t＝f(s)≤f(e)＝e2，矛盾．‎ 所以s>e，即u>1，从而ln u>0成立．‎ 另一方面，令F(u)＝ln u－，u>1.F′(u)＝－，令F′(u)＝0，得u＝2.当10；当u>2时．F′(u)<0，故对u>1，F(u)≤F(2)<0，因此ln u<成立．‎ 综上，当t>e2时，有<<.‎ ‎8．B12[2013·天津卷] 已知函数f(x)＝x(1＋a|x|)，设关于x的不等式f(x＋a)f(x＋a)可解得－0.‎ 所以f(x)在(－1，0)单调递减，在(0，＋∞)单调递增．‎ ‎(2)证明：当m≤2，x∈(－m，＋∞)时，ln(x＋m)≤ln(x＋2)，故只需证明当m＝2时，f(x)>0.‎ 当m＝2时，函数f′(x)＝ex－在(－2，＋∞)单调递增．又f′(－1)<0，f′(0)>0，故f′(x)＝0在(－2，＋∞)有唯一实根x0，且x0∈(－1，0)．‎ 当x∈(－2，x0)时，f′(x)<0；当x∈(x0，＋∞)时，f′(x)>0，从而当x＝x0时，f(x)取得最小值．‎ 由f′(x0)＝0得 ex0＝，ln(x0＋2)＝－x0，‎ 故f(x)≥f(x0)＝＋x0＝>0.‎ 综上，当m≤2时，f(x)>0.‎ ‎16．D2，D5，B12[2013·新课标全国卷Ⅱ] 等差数列{an}的前n项和为Sn，已知S10＝0，S15＝25，则nSn的最小值为________．‎ ‎16．－49 　[解析] 由已知，a1＋a10＝0，a1＋a15＝d＝，a1＝－3，∴nSn＝，易得n＝6或n＝7时，nSn出现最小值．当n＝6时，nSn＝－48；n＝7时，nSn＝－49.故nSn的最小值为－49.‎ ‎10．B3，B5，B8，B12[2013·新课标全国卷Ⅱ] 已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是(　　)‎ A．x0∈R，f(x0)＝0‎ B．函数y＝f(x)的图像是中心对称图形 C．若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)单调递减 D．若x0是f(x)的极值点，则f′(x0)＝0‎ ‎10．C　[解析] x→－∞ 时，f(x)<0 ，x→＋∞ 时，f(x)>0，f(x) 连续，x0∈R ，f(x0)＝0，A正确；通过平移变换，函数可以化为f(x)＝x3＋c ，从而函数y＝f(x)的图像是中心对称图形，B正确； 若x0是f(x)的极小值点，可能还有极大值点x1 ，则f(x)在区间(x1 ，x0)单调递减．C错误．D正确．故答案为C.‎ ‎8．B12[2013·浙江卷] 已知e为自然对数的底数，设函数f(x)＝(ex－1)(x－1)k(k＝1，2)，则(　　)‎ A．当k＝1时，f(x)在x＝1处取到极小值 B．当k＝1时，f(x)在x＝1处取到极大值 C．当k＝2时，f(x)在x＝1处取到极小值 D．当k＝2时，f(x)在x＝1处取到极大值 ‎8．C　[解析] 当k＝1时，f(x)＝(ex－1)(x－1)，f′(x)＝ex(x－1)＋(ex－1)＝xex－1，则在x＝1处取不到极值．当k＝2时，f(x)＝(ex－1)(x－1)2，f′(x)＝ex(x－1)2＋(ex－1)×2(x－1)＝(x－1)(xex＋ex－2)，f′(1)＝0，f′(2)>0，f′<0，所以在x＝1处取得极小值．‎ ‎17．B11，B12[2013·重庆卷] 设f(x)＝a(x－5)2＋6ln x，其中a∈R，曲线y＝f(x)在点(1，f(1))处的切线与y轴相交于点(0，6)．‎ ‎(1)确定a的值；‎ ‎(2)求函数f(x)的单调区间与极值．‎ ‎17．解：(1)因f(x)＝a(x－5)2＋6ln x，‎ 故f′(x)＝2a(x－5)＋.‎ 令x＝1，得f(1)＝16a，f′(1)＝6－8a，‎ 所以曲线y＝f(x)在点(1，f(1))处的切线方程为y－16a＝(6－8a)(x－1)，‎ 由点(0，6)在切线上可得6－16a＝8a－6，‎ 故a＝.‎ ‎(2)由(1)知，f(x)＝(x－5)2＋6ln x(x＞0)，‎ f′(x)＝x－5＋＝，‎ 令f′(x)＝0，解得x1＝2，x2＝3.‎ 当0＜x＜2或x＞3时，f′(x)＞0，故f(x)在(0，2)，(3，＋∞)上为增函数；当2＜x＜3时，f′(x)＜0，故f(x)在(2，3)上为减函数．‎ 由此可知，f(x)在x＝2处取得极大值f(2)＝＋6ln 2，在x＝3处取得极小值f(3)＝2＋6ln 3.‎ B13　定积分与微积分基本定理　　　　　　　　　　　　　　　　　　　‎ ‎7．B13[2013·北京卷] 直线l过抛物线C：x2＝4y的焦点且与y轴垂直，则l与C所围成的图形的面积等于(　　)‎ A. B．2 ‎ C. D. ‎7．C　[解析] 由题意得直线l的方程是y＝1，代入抛物线方程得x＝±2，所以直线l与抛物线C所围成图形的面积S＝4－2dx＝4－2)＝.‎ ‎15．B13，J3，M1[2013·福建卷] 当x∈R，|x|<1时，有如下表达式：‎ ‎1＋x＋x2＋…＋xn＋…＝.‎ 两边同时积分得：∫01dx＋∫0xdx＋∫0x2dx＋…＋∫0xndx＋…＝∫0dx，‎ 从而得到如下等式：‎ ‎1×＋×＋×＋…＋×＋…＝ln 2.‎ 请根据以上材料所蕴含的数学思想方法，计算：‎ C×＋C×2＋C×3＋…＋C×＝__________．‎ ‎15.　[解析] (1＋x)n＝C＋Cx＋Cx2＋…＋Cxn，‎ 两边同时积分得C∫01dx＋C∫0xdx＋C∫0x2dx＋…＋C∫0xndx＝∫0(1＋x)ndx，‎ 得C×＋C×2＋C×3＋…＋C×n＋1＝n＋1－1.‎ ‎7．B13[2013·湖北卷] 一辆汽车在高速公路上行驶，由于遇到紧急情况而刹车，以速度v(t)＝7－3t＋(t的单位：s，v的单位：m/s)行驶至停止，在此期间汽车继续行驶的距离(单位：m)是(　　)‎ A．1＋25ln 5 B．8＋25ln C．4＋25ln 5 D．4＋50ln 2‎ ‎7．C　[解析] 令v(t)＝0，得3t2－4t－32＝0，解得t＝4，求定积分得行驶距离为s＝v(t)dt＝7－3t＋dt＝7t－t2＋25ln(1＋t))0＝4＋25ln 5，选C.‎ ‎12．B13[2013·湖南卷] 若x2dx＝9，则常数T的值为________．‎ ‎12．3　[解析] 由积分运算公式可得x2dx＝0＝T3＝9，解得T＝3.‎ ‎6．B13[2013·江西卷] 若S1＝x2dx，S2＝dx，S3＝exdx，则S1，S2，S3的大小关系为(　　)‎ A．S10，即F(x)在(－2，x1)上单调递减，在(x1，＋∞)上单调递增．故F(x)在[－2，＋∞)上的最小值为F(x1)．‎ 而F(x1)＝2x1＋2－x－4x1－2＝－x1(x1＋2)≥0.‎ 故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．‎ ‎②若k＝e2，则F′(x)＝2e2(x＋2)(ex－e－2)．‎ 从而当x>－2时，F′(x)>0，即F(x)在(－2，＋∞)上 单调递增，而F(－2)＝0，故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．‎ ‎③若k>e2，则F(－2)＝－2ke－2＋2＝－2e－2(k－e2)<0，从而当x≥－2时，f(x)≤kg(x)不可能恒成立．‎ 综上，k的取值范围是[1，e2]．‎ ‎16．B14[2013·新课标全国卷Ⅰ] 若函数f(x)＝(1－x2)(x2＋ax＋b)的图像关于直线x＝－2对称，则f(x)的最大值为________．‎ ‎16．16　[解析] 方法一：因为f′(x)＝－4x3－3ax2＋2(1－b)x＋a，函数f(x)是连续可导函数，且关于直线x＝－2对称，所以f′(－2)＝0，即f′(－2)＝32－12a－4(1－b)＋a＝0，可得11a－4b＝28，①‎ 又因为f(0)＝f(－4)，所以15a－4b＝60，②‎ ‎①②联立方程组可得a＝8，b＝15，‎ f(x)＝(1－x2)(x2＋8x＋15)，f′(x)＝－4(x3＋6x2＋7x－2)，‎ 因为－2是函数f(x)的一个极值点，所以f′(x)＝－4(x＋2)，‎ 可知当x∈时，f(x)单调递增，当x∈时，f(x)单调递减，当x∈时，f(x)单调递增，当x∈时，f(x)单调递减，且 f＝f，所以f＝f＝f＝＝80－64＝16.‎ 方法二：令f＝0可得x＝1或x＝－1，因为函数f(x)的图像关于直线x＝－2对称，所以，可得以下同方法一．‎ ‎20．C4，C9，B14[2013·福建卷] 已知函数f(x)＝sin(ωx＋φ)(ω>0，0<φ<π)的周期为π，图像的一个对称中心为.将函数f(x)图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)，再将所得到的图像向右平移个单位长度后得到函数g(x)的图像．‎ ‎(1)求函数f(x)与g(x)的解析式；‎ ‎(2)是否存在x0∈，使得f(x0)，g(x0)，f(x0)g(x0)按照某种顺序成等差数列？若存在，请确定x0的个数；若不存在，说明理由；‎ ‎(3)求实数a与正整数n，使得F(x)＝f(x)＋ag(x)在(0，nπ)内恰有2013个零点．‎ ‎20．解：(1)由函数f(x)＝sin(ωx＋φ)的周期为π，ω>0，得ω＝＝2.‎ 又曲线y＝f(x)的一个对称中心为，φ∈(0，π)，‎ 故f＝sin＝0，得φ＝，所以f(x)＝cos 2x.‎ 将函数f(x)图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y＝cos x的图像，再将y＝cos x的图像向右平移个单位长度后得到函数g(x)＝cos的图像，所以g(x)＝sin x.‎ ‎(2)当x∈时，cos 2x>sin xcos 2x.‎ 问题转化为方程2cos 2x＝sin x＋sin xcos 2x在内是否有解．‎ 设G(x)＝sin x＋sin xcos 2x－2cos 2x，x∈，‎ 则G′(x)＝cos x＋cos xcos 2x＋2sin 2x(2－sin x)．‎ 因为x∈，所以G′(x)>0，G(x)在内单调递增．‎ 又G＝－<0，G＝>0，‎ 且函数G(x)的图像连续不断，故可知函数G(x)在内存在唯一零点x0，‎ 即存在唯一的x0∈满足题意．‎ ‎(3)方法一：依题意，F(x)＝asinx＋cos 2x，令F(x)＝asin x＋cos 2x＝0.‎ 当sin x＝0，即x＝kπ(k∈Z)时，cos2x＝1，从而x＝kπ(k∈Z)不是方程F(x)＝0的解，所以方程F(x)＝0等价于关于x的方程a＝－，x≠kπ(k∈Z)．‎ 现研究x∈(0，π)∪(π，2π)时方程a＝－的解的情况．‎ 令h(x)＝－，x∈(0，π)∪(π，2π)，‎ 则问题转化为研究直线y＝a与曲线y＝h(x)，x∈(0，π)∪(π，2π)的交点情况．‎ h′(x)＝，令h′(x)＝0，得x＝或x＝.‎ 当x变化时，h′(x)，h(x)的变化情况如下表：‎ x h′(x)‎ ‎＋‎ ‎0‎ ‎－‎ ‎－‎ ‎0‎ ‎＋‎ h(x)‎  ‎1‎   ‎－1‎  当x>0且x趋近于0时，h(x)趋向于－∞，‎ 当x<π且x趋近于π时，h(x)趋向于－∞，‎ 当x>π且x趋近于π时，h(x)趋向于＋∞，‎ 当x<2π且x趋近于2π时，h(x)趋向于＋∞，‎ 故当a>1时，直线y＝a与曲线y＝h(x)在(0，π)内无交点，在(π，2π)内有2个交点；‎ 当a<－1时，直线y＝a与曲线y＝h(x)在(0，π)内有2个交点，在(π，2π)内无交点；‎ 当－10，p(－1)＝－a－1，p(1)＝a－1.‎ 当a>1时，函数p(t)有一个零点t1∈(－1，0)(另一个零点t2>1，舍去)，F(x)在(0，2π]上有两个零点x1，x2，且x1，x2∈(π，2π)；‎ 当a<－1时，函数p(t)有一个零点t1∈(0，1)(另一个零点t2<－1，舍去)，F(x)在(0，2π]上有两个零点x1，x2，且x1，x2∈(0，π)；‎ 当－10，进而解得x>a－1，即f(x)在(a－1，＋∞)上是单调减函数．同理，f(x)在(0，a－1) 上是单调增函数．由于f(x)在(1，＋∞)上是单调减函数，故(1，＋∞)(a－1，＋∞)，从而a－1≤1，即a≥1.令g′(x)＝ex－a＝0，得x＝ln a．当xln a时，g′(x)>0.又g(x)在(1，＋∞)上有最小值，所以ln a>1，即a>e.‎ 综上，有a∈(e，＋∞)．‎ ‎(2)当a≤0时，g(x)必为单调增函数；当a>0时，令g′(x)＝ex－a>0，‎ 解得aln a，因为g(x)在(－1，＋∞)上是单调增函数，类似(1)有ln a≤－1，即00，得f(x)存在唯一的零点；‎ ‎(ii)当a<0时，由于f(ea)＝a－aea＝a(1－ea)<0，f(1)＝－a>0，且函数f(x)在[ea，1]上的图像不间断，所以f(x)在(ea，1)上存在零点．‎ 另外，当x>0时，f′(x)＝－a>0，故f(x)在(0，＋∞)上是单调增函数，所以f(x)只有一个零点．‎ ‎(iii)当00，当x>a－1时，f′(x)<0，所以，x＝a－1是f(x)的最大值点，且最大值为f(a－1)＝－ln a－1.‎ ‎①当－ln a－1＝0，即a＝e－1时，f(x)有一个零点x＝e.‎ ‎②当－ln a－1>0，即00，且函数f(x)在[e－1，a－1]‎ 上的图像不间断，所以f(x)在(e－1，a－1)上存在零点．‎ 另外，当x∈(0，a－1)时，f′(x)＝－a>0，故f(x)在(0，a－1)上是单调增函数，所以f(x)在(0，a－1)上只有一个零点．‎ 下面考虑f(x)在(a－1，＋∞)上的情况，先证f(ea－1)＝a(a－2－ea－1)<0，为此，我们要证明：当x>e时，ex>x2，设h(x)＝ex－x2，则h′(x)＝ex－2x，再设l(x)＝h′(x)＝ex－2x，则l′(x)＝ex－2.‎ 当x>1时，l′(x)＝ex－2>e－2>0，所以l(x)＝h′(x)在(1，＋∞)上是单调增函数．故当x>2时，h′(x)＝ex－2x>h′(2)＝e2－4>0，‎ 从而h(x)在(2，＋∞)上是单调增函数，进而当x>e时，h(x)＝ex－x2>h(e)＝ee－e2>0，‎ 即当x>e时，ex>x2.‎ 当0e时，f(ea－1)＝a－1－aea－1＝a(a－2－ea－1)<0，‎ 又f(a－1)>0，且函数f(x)在[a－1，ea－1]上的图像不间断，所以f(x)在(a－1，ea－1)上存在零点．‎ 又当x>a－1时，f′(x)＝－a<0，‎ 故f(x)在(a－1，＋∞)上是单调减函数，所以f(x)在(a－1，＋∞)上只有一个零点．‎ 综合(i)(ii)(iii)，当a≤0或a＝e－1时，f(x)的零点个数为1，‎ 当00)图像上一动点．若点P，A之间的最短距离为2 ，则满足条件的实数a的所有值为________．‎ ‎13．－1，　[解析] 由题意知，若a<0，则a＝－1满足题意；若a>0，则圆(x－a)2＋(y－a)2＝8与y＝(x>0)相切．联立方程，消去y得 x2－2ax＋a2＋－＋a2＝8，‎ 即－2a＋2a2－10＝0.‎ 令Δ＝0得(2a)2－4(2a2－10)＝0.(*)‎ 解得a＝.‎ 此时方程(*)的解为x＝，满足题意．‎ 综上，实数a的所有值为－1，.‎ ‎12．C9、B14[2013·全国卷] 已知函数f(x)＝cos xsin 2x，下列结论中错误的是(　　)‎ A．y＝f(x)的图像关于点(π，0)中心对称 B．y＝f(x)的图像关于直线x＝对称 C．f(x)的最大值为 D．f(x)既是奇函数，又是周期函数 ‎12．C　[解析] 因为对任意x，f(π－x)＋f(π＋x)＝cos xsin 2x－cos xsin 2x＝0，故函数f(x)图像关于点(π，0)中心对称；因为对任意x恒有f(π－x)＝cos xsin 2x＝f(x)，故函数f(x)‎ 图像关于直线x＝对称；f(－x)＝－f(x)，f(x＋2π)＝f(x)，故f(x)既是奇函数也是周期函数；对选项C中，f(x)＝2cos2xsin x＝2(1－sin2x)sin x，令t＝sin x∈[－1，1]，设y＝(1－t2)t＝－t3＋t，y′＝－3t2＋1，可得函数y的极大值点为t＝，所以y在上的极大值为－＋＝，函数的端点值为0，故函数y在区间的最大值为，函数f(x)的最大值为，所以选项C中的结论错误．‎ ‎21．B12，B14[2013·新课标全国卷Ⅱ] 已知函数f(x)＝ex－ln(x＋m)．‎ ‎(1)设x＝0是f(x)的极值点，求m，并讨论f(x)的单调性；‎ ‎(2)当m≤2时，证明f(x)＞0.‎ ‎21．解：(1)f′(x)＝ex－.‎ 由x＝0是f(x)的极值点得f′(0)＝0，所以m＝1.‎ 于是f(x)＝ex－ln(x＋1)，定义域为(－1，＋∞)，f′(x)＝ex－.‎ 函数f′(x)＝ex－在(－1，＋∞)单调递增，‎ 且f′(0)＝0，因此当x∈(－1，0)时，‎ f′(x)<0；当x∈(0，＋∞)时，f′(x)>0.‎ 所以f(x)在(－1，0)单调递减，在(0，＋∞)单调递增．‎ ‎(2)证明：当m≤2，x∈(－m，＋∞)时，ln(x＋m)≤ln(x＋2)，故只需证明当m＝2时，f(x)>0.‎ 当m＝2时，函数f′(x)＝ex－在(－2，＋∞)单调递增．又f′(－1)<0，f′(0)>0，故f′(x)＝0在(－2，＋∞)有唯一实根x0，且x0∈(－1，0)．‎ 当x∈(－2，x0)时，f′(x)<0；当x∈(x0，＋∞)时，f′(x)>0，从而当x＝x0时，f(x)取得最小值．‎ 由f′(x0)＝0得 ex0＝，ln(x0＋2)＝－x0，‎ 故f(x)≥f(x0)＝＋x0＝>0.‎ 综上，当m≤2时，f(x)>0.‎ ‎22．B14[2013·浙江卷] 已知a∈R，函数f(x)＝x3－3x2＋3ax－3a＋3.‎ ‎(1)求曲线y＝f(x)在点(1，f(1))处的切线方程；‎ ‎(2)当x∈[0，2]时，求|f(x)|的最大值．‎ ‎22．解：(1)由题意 f′(x)＝3x2－6x＋3a，故 f′(1)＝3a－3.‎ 又f(1)＝1，所以所求的切线方程为y＝(3a－3)x－3a＋4.‎ ‎(2)由于f′(x)＝3(x－1)2＋3(a－1)，0≤x≤2，故 ‎①当a≤0时，有f′(x)≤0，此时f(x)在[0，2]上单调递减，故 ‎|f(x)|max＝max {|f(0)|，|f(2)|}＝3－3a.‎ ‎②当a≥1时，有f′(x)≥0，此时f(x)在[0，2]上单调递增，故 ‎|f(x)|max＝max {|f(0)|，|f(2)|}＝3a－1.‎ ‎③当00，f(x1)－f(x2)＝4(1－a)>0.‎ 从而f(x1)>|f(x2)|.‎ 所以|f(x)|max＝max{f(0)，|f(2)|，f(x1)}．‎ ‎(Ⅰ)当0|f(2)|.‎ 又f(x1)－f(0)＝2(1－a)－(2－3a)＝>0，‎ 故|f(x)|max＝f(x1)＝1＋2(1－a).‎ ‎(Ⅱ)当≤a<1时，|f(2)|＝f(2)，且f(2)≥f(0)．‎ 又f(x1)－|f(2)|＝2(1－a)－(3a－2)＝.‎ 所以(i)当≤a<时，f(x1)>|f(2)|.‎ 故f(x)max＝f(x1)＝1＋2(1－a).‎ ‎(ii)当≤a<1时，f(x1)≤|f(2)|.‎ 故f(x)max＝|f(2)|＝3a－1.‎ 综上所述，‎ ‎|f(x)|max＝