福建省莆田市2020届高三3月（线上）毕业班教学质量检测试卷数学（理）试题 Word版含解析 24页

www.ks5u.com ‎2020年莆田市高中毕业班教学质量检测试卷 数学（理科）‎ 本试卷分Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.本试卷共5页.满分150分.考试时间120分钟.‎ 注意事项：‎ ‎1.答题前，考生先将自己的姓名、准考证号填写在答题卡上.‎ ‎2.考生作答时，将答案答在答题卡上.请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效.在草稿纸、试题卷上答题无效.‎ ‎3.选择题答案使用2B铅笔填涂,如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚.‎ ‎4.保持答题卡卡面清洁，不折叠、不破损.考试结束后，将本试卷和答题卡一并交回.‎ 第Ⅰ卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知集合，，则（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 计算，，再计算得到答案.‎ ‎【详解】，，‎ 故.‎ 故选：.‎ ‎【点睛】本题考查了交集运算，意在考查学生的计算能力.‎ ‎2.若i•z＝1﹣2i，则|z|＝（ ）‎ A. B. C. 3 D. 5‎ - 24 -‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 首先利用复数的运算法则进行化简，然后再进行复数模的运算即可.‎ ‎【详解】，‎ ‎，. ‎ 故选：B.‎ ‎【点睛】本题主要考查复数的运算以及模的运算，属于基础题.首先对于复数的四则运算，要切实掌握其运算技巧和常规思路，如，，，.其次要熟悉复数相关基本概念，如复数的实部为、虚部为、模为、共轭复数为.‎ ‎3.若，，则（ ）‎ A. B. C. D. 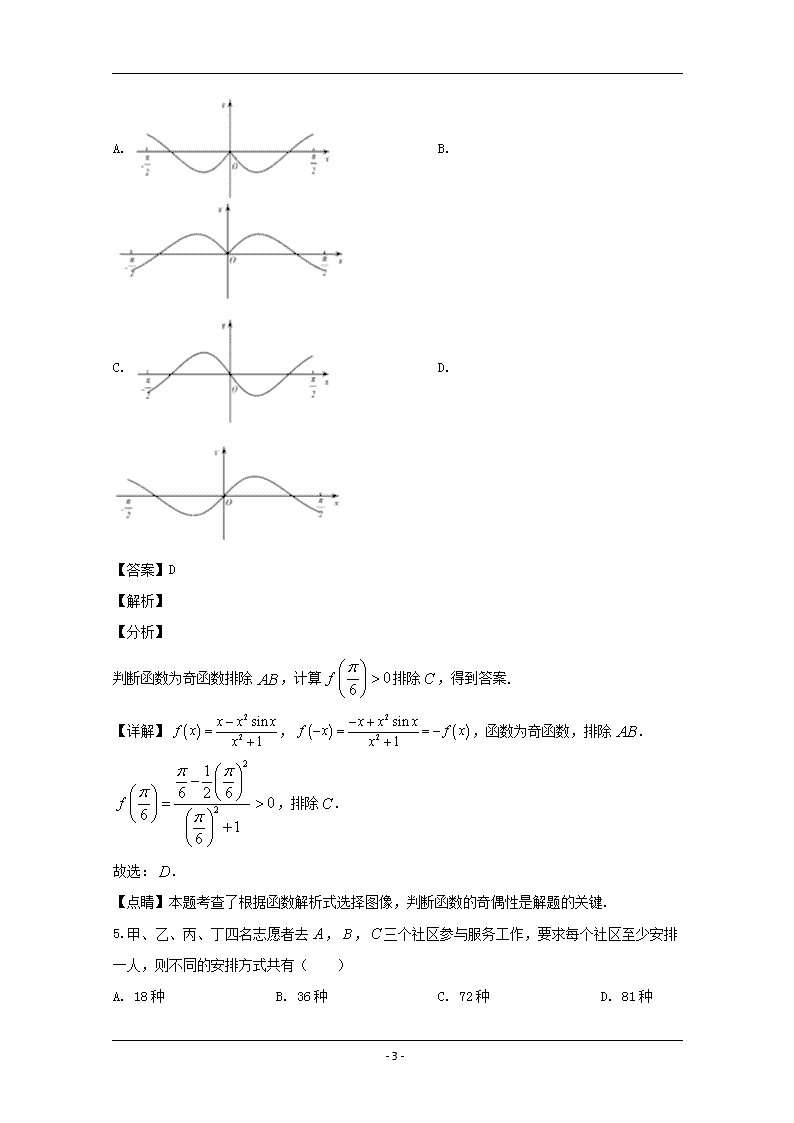‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据范围计算得到，，计算得到答案.‎ ‎【详解】，故，，故.‎ ‎，‎ 故选：.‎ ‎【点睛】本题考查了二倍角公式，同角三角函数关系，意在考查学生的计算能力.‎ ‎4.函数在的图象大致为（ ）‎ - 24 -‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 判断函数为奇函数排除，计算排除，得到答案.‎ ‎【详解】，，函数为奇函数，排除.‎ ‎，排除.‎ 故选：.‎ ‎【点睛】本题考查了根据函数解析式选择图像，判断函数的奇偶性是解题的关键.‎ ‎5.甲、乙、丙、丁四名志愿者去，，三个社区参与服务工作，要求每个社区至少安排一人，则不同的安排方式共有（ ）‎ A. 18种 B. 36种 C. 72种 D. 81种 - 24 -‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 利用捆绑法将四人分为三组有种，再全排列种，计算得到答案.‎ ‎【详解】利用捆绑法将四人分为三组：种，再全排列种，故有种不同的安排方式.‎ 故选：.‎ ‎【点睛】本题考查了排列组合中的捆绑法，意在考查学生的应用能力.‎ ‎6.高斯函数表示不超过的最大整数，如，，.执行下边的程序框图，则输出的值为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ 分析】‎ 根据程序框图依次计算得到答案.‎ ‎【详解】程序框图依次计算：；；；，结束.‎ 故选：.‎ ‎【点睛】本题考查了程序框图，意在考查学生的理解能力和计算能力.‎ ‎7.函数的图象在点切的切线分别交轴，轴于、两点，‎ - 24 -‎ 为坐标原点，，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 求导得到，计算切线方程为，故，，代入向量计算得到答案.‎ ‎【详解】，，故，，，‎ 故切线方程为：，故，.‎ ‎，即，解得.‎ 故选：.‎ ‎【点睛】本题考查了切线方程，向量运算，意在考查学生的计算能力和综合应用能力.‎ ‎8.已知函数f（x）＝sin（ωx+φ）（ω＞0，0＜φ＜π）的图象关于直线x对称，且.当ω取最小值时，φ＝（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由正弦函数的对称轴和对称中心并结合正弦函数的图象，求得取最小值时，然后利用求出的值.‎ ‎【详解】函数的图象关于直线对称，且 - 24 -‎ ‎，‎ 则取最小时，，‎ 可得，可得，‎ 再根据，‎ 可得，，求得，，‎ 因为，‎ 所以，‎ 故选：D.‎ ‎【点睛】本题主要考查正弦函数的图象和性质，主要考查函数的对称性和周期性，意在考查学生对这些基础知识的掌握能力和数形结合的思想方法，属于中档题．‎ ‎9.已知抛物线的焦点为，过的直线交于，两点，轴被以为直径的圆所截得的弦长为6，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 故设直线为，设，，计算得到中点的横坐标为，，根据，计算得到答案.‎ ‎【详解】抛物线的焦点，易知当斜率不存在时不成立，‎ 故设直线为，设，.‎ 则，即，故，‎ - 24 -‎ 故中点的横坐标为，.‎ 故，解得，故.‎ 故选：.‎ ‎【点睛】本题考查了抛物线中的弦长问题，直线和圆的位置关系，意在考查学生的转化能力和计算能力.‎ ‎10.已知三棱锥的四个顶点在球的球面上，平面，，与平面所成的角为，则球的表面积为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 取中点，连接，证明平面，故为与平面所成的角为，球心在平面的投影为的外心，计算得到答案.‎ ‎【详解】取中点，连接，，则.‎ 平面，平面，故.‎ ‎，故平面，故为与平面所成的角为.‎ ‎，故，，，故.‎ 球心在平面的投影为的外心，‎ 根据知，，故，‎ 故球的表面积为.‎ 故选：.‎ - 24 -‎ ‎【点睛】本题考查了三棱锥的外接球问题，确定球心在平面的投影为的外心是解题的关键，意在考查学生的计算能力和空间想象能力.‎ ‎11.已知双曲线的左、右焦点分别为，过的直线与的左支交于，两点，若，且，则的离心率为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 计算得到，， ，，根据，利用余弦定理得到，计算得到答案.‎ ‎【详解】，故，‎ ‎，故，故.‎ 根据余弦定理，‎ ‎，，‎ 化简整理得到：，即，解得或（舍去）.‎ 故选：.‎ - 24 -‎ ‎【点睛】本题考查了双曲线离心率，意在考查学生的计算能力和综合应用能力.‎ ‎12.设函数的定义域为，已知有且只有一个零点.下列四个结论：‎ ‎①； ②在区间单调递增；‎ ‎③是的零点； ④是的极大值点，是的最小值.‎ 其中正确的个数是（ ）‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 取，即，两边取对数，设，求导画出函数图像，计算，故，画出函数和的图像，根据图像得到函数单调性，依次判断每个选项得到答案.‎ ‎【详解】取，即，两边取对数，‎ 即有且只有一个解，设，.‎ 函数在上单调递增，在上单调递减，画出函数图像，如图所示：‎ 故或，解得或（舍去），故，①正确；‎ ‎，，③正确，‎ ‎，取，即，‎ 两边取对数，画出函数和的图像，‎ 根据图像知：‎ 当时，，故，函数单调递减；‎ 当或时，，函数单调递增.‎ 故②错误，④正确.‎ 故选：.‎ - 24 -‎ ‎【点睛】本题考查了利用导数求参数值，函数的单调性，极值，零点问题，意在考查学生的综合应用能力.‎ 第Ⅱ卷 本卷包括必考题和选考题两部分.第13~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.‎ ‎13.已知非零向量，满足，且，则与的夹角为__________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据得到，计算得到答案.‎ ‎【详解】，故，故，即.‎ 故答案为：.‎ ‎【点睛】本题考查了向量夹角的计算，意在考查学生的计算能力.‎ - 24 -‎ ‎14.设满足约束条件则的最大值为__________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 画出可行域，表示点和之间的斜率，根据图像得到答案.‎ ‎【详解】如图所示，画出可行域，表示点和之间的斜率.‎ 根据图像知：当时，有最大值为.‎ 故答案为：.‎ ‎【点睛】本题考查了线性规划问题，将表示为两点的斜率是解题的关键.‎ ‎15.已知函数且，则__________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 讨论和两种情况，分别计算得到，再代入计算得到答案.‎ - 24 -‎ ‎【详解】当时，，，不成立；‎ 当时，，或（舍去）；‎ 综上所述：，.‎ 故答案为：.‎ ‎【点睛】本题考查了分段函数求参数和函数值，意在考查学生的计算能力.‎ ‎16.的内角，，，的对边分别为，，.已知，是边上的中线，且，则面积的最大值为__________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据正弦定理计算得到，设，则，，根据余弦定理得到，故，计算得到答案.‎ ‎【详解】，即，即，‎ 故，，故.‎ 设，则，，‎ 在中：根据余弦定理，，即.‎ ‎，‎ 故，‎ 当，即，面积有最大值为.‎ 故答案为：.‎ ‎【点睛】本题考查了正弦定理，余弦定理，面积公式，意在考查学生的综合应用能力.‎ - 24 -‎ 三、解答题：共70分.解答应写岀文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.‎ ‎（一）必考题：（60分）‎ ‎17.设是公差不为0的等差数列，其前项和为已知，，成等比数列，.‎ ‎（1）求的通项公式;‎ ‎（2）设，数列的前项和为，求.‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据题意得到，，计算得到答案.‎ ‎（2），利用分组求和法计算得到答案.‎ ‎【详解】（1），，成等比数列，故，即.‎ ‎，解得，故.‎ ‎（2）.‎ ‎.‎ ‎【点睛】本题考查了数列的通项公式，前项和，意在考查学生对于数列公式方法的综合应用.‎ ‎18.如图，四棱锥的底面是菱形，，，.‎ ‎（1）证明：平面平面；‎ - 24 -‎ ‎（2）若，点在棱上，且，求二面角的余弦值.‎ ‎【答案】（1）证明见解析；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）连接与相交于，根据，得到平面，得到证明.‎ ‎（2）以为轴建立空间直角坐标系，设，根据得到，计算平面的法向量为，平面的法向量为，计算夹角得到答案.‎ ‎【详解】（1）如图所示：连接与相交于，，故，‎ 四棱锥的底面是菱形，故，，故平面，‎ 平面，故平面平面.‎ ‎（2），故平面，取中点，连接，故.‎ 以为轴建立空间直角坐标系，如图所示：‎ 则，设，‎ ‎，解得，，.‎ ‎，‎ ‎，，，‎ 故，‎ 解得或（舍去），.‎ 设平面法向量为，‎ 则，取，‎ - 24 -‎ 设平面的法向量为，‎ 则，取，，‎ 设二面角的平面角为，则.‎ ‎【点睛】‎ 本题考查了面面垂直，二面角，意在考查学生的空间想象能力和计算能力.‎ ‎19.莆田市是福建省“历史文化名城”之一，也是旅游资源丰富的城市.“九头十八巷”、“二十四景”美如画.某文化传媒公司为了解莆田民众对当地风景民俗知识的了解情况，在全市进行网上问卷（满分100分）调查，民众参与度极高.该公司对得分数据进行统计拟合，认为服从正态分布.‎ ‎（1）从参与调查的民众中随机抽取200名作为幸运者，试估算其中得分在75分以上（含75分）的人数（四舍五入精确到1人）；‎ ‎（2）在（1）的条件下，为感谢参与民众，该公司组织两种活动，得分在75分以上（含75分）的幸运者选择其中一种活动参与.活动如下：‎ - 24 -‎ 活动一 参与一次抽奖.已知抽中价值200元的礼品的概率为，抽中价值420元的礼品的概率为；‎ 活动二 挑战一次闯关游戏.规则如下：游戏共有三关，闯关成功与否相互独立，挑战者依次闯关，第一关闯关失败者没有获得礼品，第二关起闯关失败者只能获得上一关的礼品，获得的礼品不累计，闯关结束.已知第一关通过的概率为，可获得价值300元的礼品；第二关通过的概率为，可获得价值800元的礼品；第三关通过的概率为，可获得价值1800元的礼品.‎ 若参与活动的幸运者均选择礼品价值期望值较高的活动，该公司以该期望值为依据，需准备多少元的礼品？‎ 附：若，则，，‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）计算得到，，故，计算得到答案.‎ ‎（2）计算，活动二的取值可能有，，，，计算概率得到分布列，得到，计算得到答案.‎ ‎【详解】（1）服从正态分布，则，，‎ ‎，‎ 故，故人数为.‎ ‎（2）活动一的数学期望为：；‎ 活动二的取值可能有，，，，‎ 故，，，‎ - 24 -‎ ‎.‎ 分布列为：‎ 故.‎ ‎，故需要准备元礼物.‎ ‎【点睛】本题考查了正态分布，分布列，数学期望，意在考查学生的计算能力和应用能力.‎ ‎20.已知为椭圆的左、右焦点，点在上.有以下三个条件：①；②点的坐标为；③且.‎ ‎（1）从三个条件中任意选择两个，求的方程；‎ ‎（2）在（1）的条件下，过点的直线与交于，两点，关于坐标原点的对称点为，求面积的最大值.‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）取条件①和②，则，，解得答案.‎ ‎（2），设直线方程为，，，，联立方程得到，，，设，故，利用均值不等式得到答案.‎ ‎【详解】（1）取条件①和②，则，，解得，故椭圆方程为 - 24 -‎ ‎.‎ ‎（2）易知直线斜率不为，设直线方程为，，，，‎ 故，即，，.‎ ‎，‎ 设，，故.‎ 当且仅当，即时等号成立，此时验证成立，故面积最大值.‎ ‎【点睛】本题考查了椭圆方程，面积的最值问题，意在考查学生的计算能力和转化能力.‎ ‎21.已知函数，.‎ ‎（1）求在区间的极值点；‎ ‎（2）证明：在区间有且只有3个零点，且之和为0.‎ ‎【答案】（1）或；（2）证明见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）求导取，得到或，再根据单调性得到极值点.‎ ‎（2）化简得到，得到若是方程的根据，那么也是方程的根，画出函数和的图像，根据图像得到答案.‎ - 24 -‎ ‎【详解】（1），则，‎ 取，则或.‎ 当时，，函数单调递增；当时，，函数单调递减；‎ 当时，，函数单调递增，故极值点为或.‎ ‎（2），故.‎ ‎，即，‎ ‎，，.‎ 若是方程的根，那么也是方程的根，故零点之和为.‎ 画出函数和的图像，如图所示：‎ 根据图像知函数图像有三个交点，故在区间有且只有3个零点.‎ 综上所述：在区间有且只有3个零点，且之和为0.‎ - 24 -‎ ‎【点睛】本题考查了函数的极值点，零点问题，画出函数图像是解题的关键，意在考查学生的计算能力和综合应用能力.‎ ‎（二）选考题：共10分.请考生在第2、23题中任选一题作答.注意：只能做所选定的题目.如果多做，则按所做第一个题目计分，作答时请用2B铅笔在答题卡上将所选题号后的方框涂黑.‎ ‎22.在直角坐标系xOy中，已知直线l过点P（2，2）.以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ﹣ρcos2θ﹣4cosθ＝0.‎ ‎（1）求C的直角坐标方程；‎ ‎（2）若l与C交于A，B两点，求的最大值.‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）把曲线的极坐标方程两边同时乘以，结合，，，即可求出曲线的极坐标方程；‎ ‎（2）由已知直接写出直线的参数方程，把直线的参数方程代入曲线的极坐标方程，化为关于的一元二次方程，利用根与系数的关系及参数的几何意义求解.‎ ‎【详解】（1）曲线的极坐标方程为，两边同时乘以，得 - 24 -‎ ‎，把互化公式代入可得：，即，所以C的直角坐标方程为y2＝4x.‎ ‎（2）设直线的倾斜角为，可得参数方程为：（为参数），代入抛物线方程可得：，‎ 则，，‎ ‎∴，‎ 当且仅当时，等号成立，‎ 的最大值为.‎ ‎【点睛】1.极坐标方程转化为普通方程，要巧用极坐标方程两边同乘以或同时平方技巧，将极坐标方程构造成含有，，的形式，然后利用公式代入化简得到普通方程；‎ ‎2.经过点，倾斜角为的直线的参数方程为（为参数）.若A，B为直线上两点，其对应的参数分别为，，线段的中点为，点所对应的参数为，则以下结论在解题中经常用到：‎ ‎（1）；‎ ‎（2）；‎ ‎（3）；‎ ‎（4）.‎ ‎23.已知f（x）＝|2x﹣1|+|x+2|.‎ ‎（1）求不等式f（x）≤5的解集；‎ ‎（2）若x∈[﹣1，+∞）时，f（x）≥kx+k，求k的取值范围.‎ - 24 -‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）可先将写成分段形式，从而求得解集；‎ ‎（2）时，成立；时，，等价于，令，故即可，从而求得答案.‎ ‎【详解】（1）由，‎ 不等式等价于，‎ 可化为，‎ 或 或；‎ 解得，‎ 所以不等式的解集是；‎ ‎（2）当时，成立，；‎ 当时，，所以，‎ 即，所以；‎ 当时，，所以，‎ 即k，所以；‎ - 24 -‎ 综上知，的取值范围是.‎ ‎【点睛】1.求解绝对值不等式的步骤：‎ ‎（1）求零点；‎ ‎（2）划区间，去绝对值符号；‎ ‎（3）分别解去掉绝对值符号的不等式；‎ ‎（4）取每个结果的并集，注意在分段讨论时，不要遗漏区间的端点值.‎ ‎2.绝对值不等式有解问题的求解思路：‎ ‎（1）分离参数：根据不等式，将参数分离化为或的形式；‎ ‎（2）转化为最值问题：恒成立，恒成立；‎ ‎（3）得结论.‎ ‎ ‎ - 24 -‎ - 24 -‎