2020高中数学 第一章 三角函数 4页

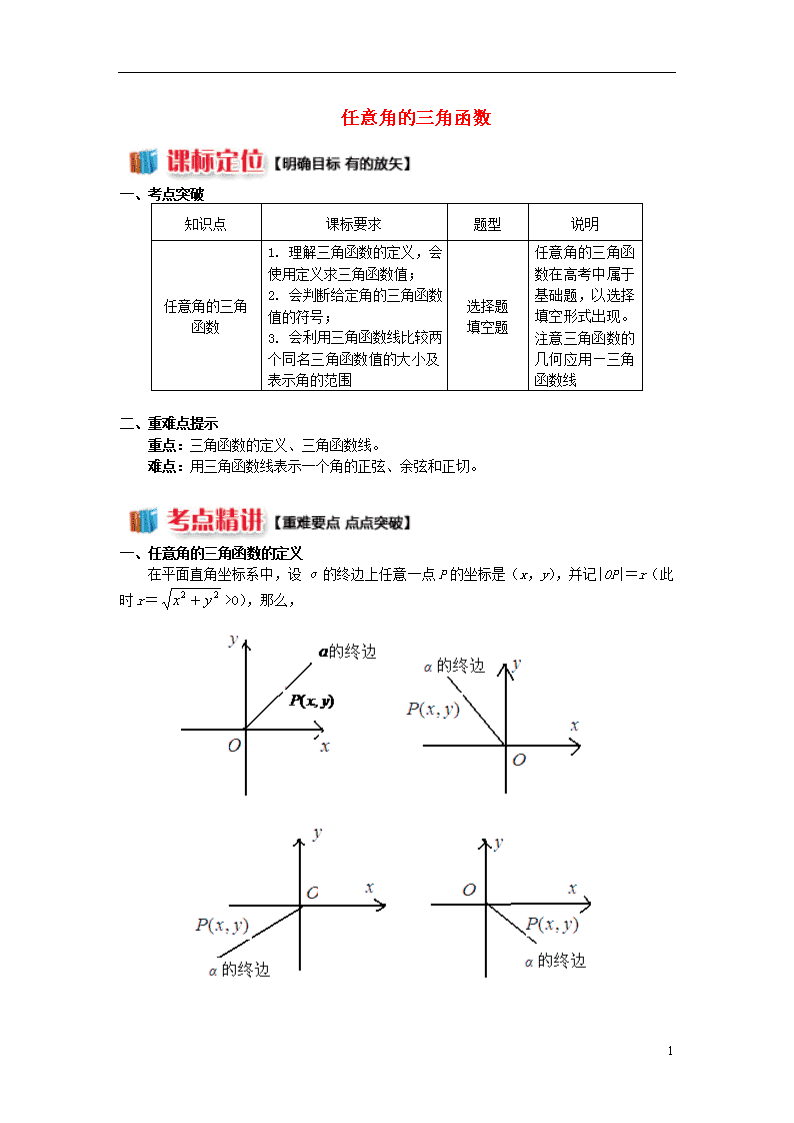
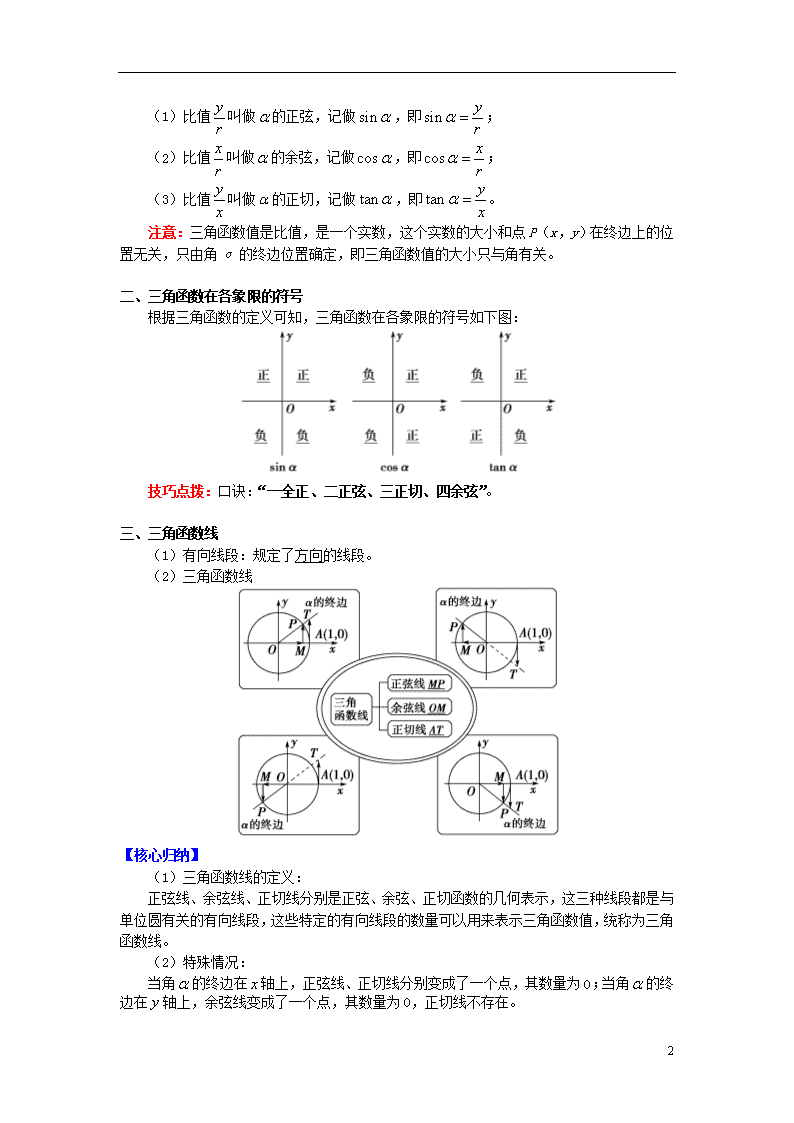
任意角的三角函数 一、考点突破 知识点 课标要求 题型 说明 任意角的三角函数 ‎1. 理解三角函数的定义，会使用定义求三角函数值；‎ ‎2. 会判断给定角的三角函数值的符号；‎ ‎3. 会利用三角函数线比较两个同名三角函数值的大小及表示角的范围 选择题 填空题 ‎ 任意角的三角函数在高考中属于基础题，以选择填空形式出现。注意三角函数的几何应用—三角函数线 二、重难点提示 重点：三角函数的定义、三角函数线。‎ 难点：用三角函数线表示一个角的正弦、余弦和正切。‎ 一、任意角的三角函数的定义 在平面直角坐标系中，设α的终边上任意一点P的坐标是（x，y），并记|OP|＝r（此时r＝>0），那么，‎ 4‎ ‎（1）比值叫做的正弦，记做，即；‎ ‎（2）比值叫做的余弦，记做，即；‎ ‎（3）比值叫做的正切，记做，即。‎ 注意：三角函数值是比值，是一个实数，这个实数的大小和点P（x，y）在终边上的位置无关，只由角α的终边位置确定，即三角函数值的大小只与角有关。‎ 二、三角函数在各象限的符号 根据三角函数的定义可知，三角函数在各象限的符号如下图：‎ 技巧点拨：口诀：“一全正、二正弦、三正切、四余弦”。‎ 三、三角函数线 ‎（1）有向线段：规定了方向的线段。‎ ‎（2）三角函数线 ‎【核心归纳】‎ ‎（1）三角函数线的定义：‎ 正弦线、余弦线、正切线分别是正弦、余弦、正切函数的几何表示，这三种线段都是与单位圆有关的有向线段，这些特定的有向线段的数量可以用来表示三角函数值，统称为三角函数线。‎ ‎（2）特殊情况：‎ 当角的终边在轴上，正弦线、正切线分别变成了一个点，其数量为0；当角的终边在轴上，余弦线变成了一个点，其数量为0，正切线不存在。‎ 4‎ ‎（3）三角函数线的主要作用 解三角不等式及比较同角异名三角函数值的大小，同时它也是以后学习三角函数的图象和性质的基础。‎ 例题1 （青岛）已知角θ的终边上有一点P（－，m），且sin θ＝m，求cos θ与tan θ的值。‎ 思路分析：先利用三角函数定义sin θ＝，求出m的值，再用公式cos θ＝，tan θ＝代入数据求解。‎ 答案：由已知r＝＝，‎ ‎∴，解得m＝0，或m＝±，‎ ‎（1）当m＝0时，cos θ＝－1，tan θ＝0；‎ ‎（2）当m＝时，cos θ＝－，tan θ＝－；‎ ‎（3）当m＝－时，cos θ＝－，tan θ＝。‎ 技巧点拨：‎ ‎1. 利用三角函数的定义求一个角的三角函数值需明确三个量：角的终边上任意一个异于原点的点的横坐标x，纵坐标y，该点到原点的距离r。‎ ‎2. 当角α的终边上点的坐标以参数形式给出时，要根据问题的实际情况对参数进行分类讨论。‎ 例题2 在单位圆中画出适合下列条件的角α的终边范围，并由此写出角α的集合。‎ ‎（1）sin α≥；（2）cos α≤－。‎ 思路分析：根据三角函数线，在单位圆中首先作出满足sin α＝，cos α＝－的角的终边，然后由已知条件确定角α的终边范围。‎ 答案：（1）作直线y＝交单位圆于A，B两点，连接OA，OB，则OA与OB围成的区域（如图①阴影部分）即为角α的终边的范围，‎ 故满足条件的角α的集合为{α|2kπ＋≤α≤2kπ＋，k∈Z}，‎ 4‎ ‎（2）作直线x＝－交单位圆于C，D两点，连接OC与OD，则OC与OD围成的区域（如图②阴影部分）即为角α的终边的范围，‎ 故满足条件的角α的集合为{α|2kπ＋≤α≤2kπ＋，k∈Z}。‎ 技巧点拨：三角函数线是利用数形结合思想解决有关问题的有力工具。‎ 忽视角所在象限的讨论致误 ‎【满分训练】已知角α的顶点在原点上，始边与x轴的非负半轴重合，终边上一点的坐标为（‎3a，‎4a）（a≠0），求角α的正弦值和正切值。‎ 错解：由题意得x＝‎3a，y＝‎4a，‎ 所以r＝＝＝‎5a，‎ 所以sin α＝＝＝，tan α＝＝＝。‎ 错因分析：本题中点的坐标含参数，当a＞0时，该点在第一象限，即角α的终边在第一象限；当a＜0时，该点在第三象限，即角α的终边在第三象限，故应对a的取值范围进行分类讨论。‎ 防范措施：根据角的终边上一点的坐标求三角函数值时，若坐标中含有字母，则应分类讨论。‎ 正解：由题意得x＝‎3a，y＝‎4a，‎ 所以r＝＝＝5|a|，‎ 若a＞0，则r＝‎5a，‎ 所以sin α＝，‎ tan α＝＝＝；‎ 若a＜0，则r＝－‎5a，‎ 所以sin α＝＝＝－，‎ tan α＝＝＝。‎ 技巧点拨：开方运算时注意这一结论。‎ 4‎