高中数学人教a版选修2-2（课时训练）：第一章 导数及其应用 章末复习 word版含答案 9页

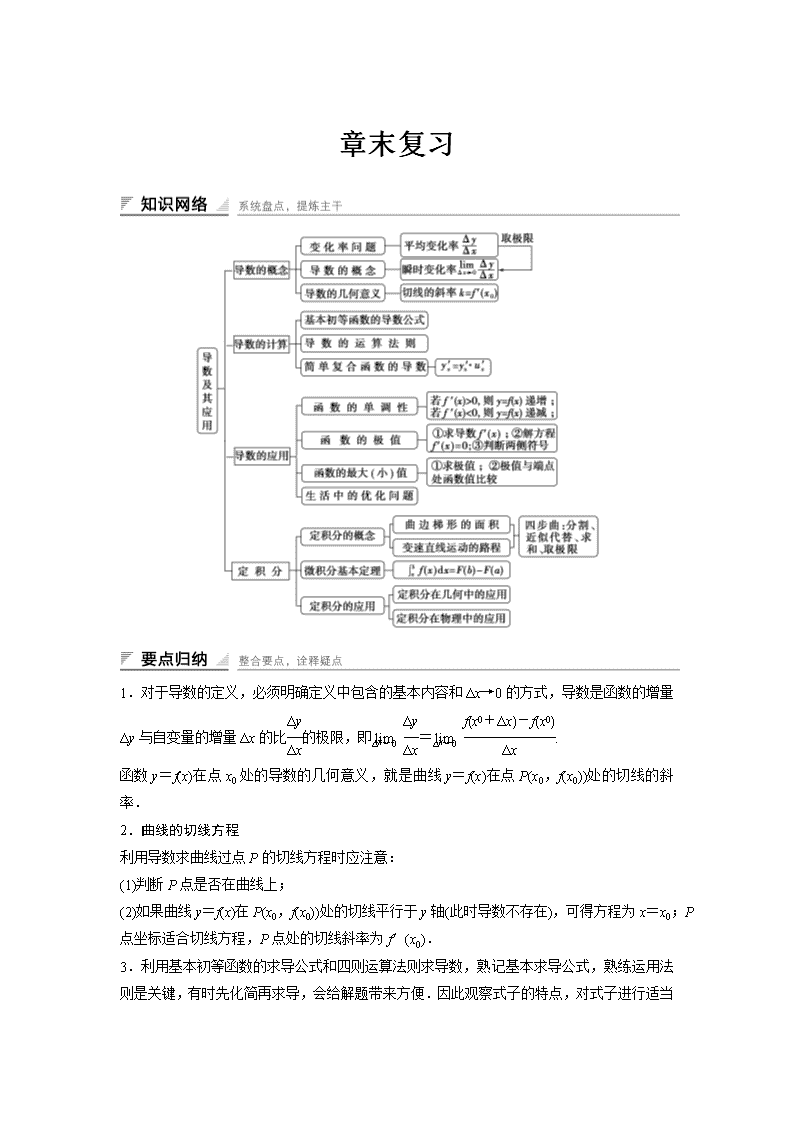
章末复习 1．对于导数的定义，必须明确定义中包含的基本内容和Δx→0 的方式，导数是函数的增量 Δy 与自变量的增量Δx 的比Δy Δx 的极限，即limΔx→0 Δy Δx ＝limΔx→0 fx0＋Δx－fx0 Δx . 函数 y＝f(x)在点 x0 处的导数的几何意义，就是曲线 y＝f(x)在点 P(x0，f(x0))处的切线的斜率． 2．曲线的切线方程 利用导数求曲线过点 P 的切线方程时应注意： (1)判断 P 点是否在曲线上； (2)如果曲线 y＝f(x)在 P(x0，f(x0))处的切线平行于 y 轴(此时导数不存在)，可得方程为 x＝x0； P 点坐标适合切线方程，P 点处的切线斜率为 f′(x0)． 3．利用基本初等函数的求导公式和四则运算法则求导数，熟记基本求导公式，熟练运用法 则是关键，有时先化简再求导，会给解题带来方便．因此观察式子的特点，对式子进行适当 的变形是优化解题过程的关键． 4．判断函数的单调性 (1)在利用导数讨论函数的单调区间时，首先要确定函数的定义域，解决问题的过程中，只 能在函数的定义域内，通过讨论导数的符号，来判断函数的单调区间； (2)注意在某一区间内 f′(x)＞0(或 f′(x)＜0)是函数 f(x)在该区间上为增(或减)函数的充分条 件． 5．利用导数研究函数的极值要注意 (1)极值是一个局部概念，是仅对某一点的左右两侧领域而言的． (2)连续函数 f(x)在其定义域上的极值点可能不止一个，也可能没有极值点，函数的极大值与 极小值没有必然的大小联系，函数的一个极小值也不一定比它的一个极大值小． (3)可导函数的极值点一定是导数为零的点，但函数的导数为零的点，不一定是该函数的极 值点．因此导数为零的点仅是该点为极值点的必要条件，其充要条件是加上这点两侧的导数 异号． 6．求函数的最大值与最小值 (1)函数的最大值与最小值：在闭区间[a，b]上连续的函数 f(x)，在[a，b]上必有最大值与最 小值；但在开区间(a，b)内连续的函数 f(x)不一定有最大值与最小值，例如：f(x)＝x3，x∈(－ 1,1)． (2)求函数最值的步骤 一般地，求函数 y＝f(x)在[a，b]上最大值与最小值的步骤如下： ①求函数 y＝f(x)在(a，b)内的极值； ②将函数 y＝f(x)的各极值与端点处的函数值 f(a)，f(b)比较，其中最大的一个是最大值，最 小的一个是最小值． 7．应用导数解决实际问题，关键在于建立恰当的数学模型(函数关系)，如果函数在区间内 只有一个点 x0，使 f′(x0)＝0，则 f(x0)是函数的最值. 题型一 应用导数解决与切线相关的问题 根据导数的几何意义，导数就是相应切线的斜率，从而就可以应用导数解决一些与切线相关 的问题． 例 1 (2013·福建)已知函数 f(x)＝x－aln x(a∈R)． (1)当 a＝2 时，求曲线 y＝f(x)在点 A(1，f(1))处的切线方程； (2)求函数 f(x)的极值． 解 函数 f(x)的定义域为(0，＋∞)，f′(x)＝1－a x. (1)当 a＝2 时，f(x)＝x－2ln x，f′(x)＝1－2 x(x＞0)， ∴f(1)＝1，f′(1)＝－1， ∴y＝f(x)在点 A(1，f(1))处的切线方程为 y－1＝－(x－1)，即 x＋y－2＝0. (2)由 f′(x)＝1－a x ＝x－a x ，x＞0. ①当 a≤0 时，f′(x)＞0，函数 f(x)为(0，＋∞)上的增函数，函数 f(x)无极值； ②当 a＞0 时，由 f′(x)＝0，解得 x＝a； ∵x∈(0，a)时，f′(x)＜0，x∈(a，＋∞)时，f′(x)＞0 ∴f(x)在 x＝a 处取得极小值，且极小值为 f(a)＝a－aln a，无极大值． 综上当 a≤0 时，函数 f(x)无极值；当 a＞0 时，函数 f(x)在 x＝a 处取得极小值 a－aln a，无 极大值． 跟踪演练 1 已知曲线 C 的方程是 y＝x3－3x2＋2x. (1)求曲线在 x＝1 处的切线方程； (2)若 l2：y＝kx，且直线 l2 与曲线 C 相切于点(x0，y0)(x0≠0)，求直线 l2 的方程及切点坐标． 解 (1)∵y′＝3x2－6x＋2， ∴y′|x＝1＝3×1－6×1＋2＝－1. ∴l1 的斜率为－1，且过点(1,0)． ∴直线 l1 的方程为 y＝－(x－1)， 即 l1 的方程为 x＋y－1＝0. (2)直线 l2 过原点，则 k＝y0 x0 (x0≠0)， 由点(x0，y0)在曲线 C 上，得 y0＝x30－3x20＋2x0， ∴y0 x0 ＝x20－3x0＋2. ∵y′＝3x2－6x＋2，∴k＝3x20－6x0＋2. 又 k＝y0 x0 ，∴3x20－6x0＋2＝y0 x0 ＝x20－3x0＋2， 整理得 2x20－3x0＝0.∵x0≠0，∴x0＝3 2 ， 此时 y0＝－3 8 ，k＝－1 4 ， 因此直线 l2 的方程为 y＝－1 4x，切点坐标为 3 2 ，－3 8 . 题型二 利用导数求函数的单调区间 在区间(a，b)内，如果 f′(x)>0，那么函数 y＝f(x)在区间(a，b)内单调递增；在区间(a，b) 内，如果 f′(x)<0，那么函数 y＝f(x)在区间(a，b)内单调递减． 例 2 已知函数 f(x)＝x－2 x ＋a(2－ln x)，a＞0.讨论 f(x)的单调性． 解 由题知，f(x)的定义域是(0，＋∞)， f′(x)＝1＋2 x2 －a x ＝x2－ax＋2 x2 . 设 g(x)＝x2－ax＋2，二次方程 g(x)＝0 的判别式Δ＝a2－8. ①当Δ＜0 即 0＜a＜2 2时，对一切 x＞0 都有 f′(x)＞0.此时 f(x)是(0，＋∞)上的单调递增 函数． ②当Δ＝0 即 a＝2 2时，仅对 x＝ 2，有 f′(x)＝0，对其余的 x＞0 都有 f′(x)＞0.此时 f(x) 也是(0，＋∞)上的单调递增函数． ③当Δ＞0 即 a＞2 2时，方程 g(x)＝0 有两个不同的实根 x1＝a－ a2－8 2 ，x2＝a＋ a2－8 2 ，0 ＜x1＜x2. 当 x 变化时，f′(x)、f(x)的变化情况如下表： x (0，x1) x1 (x1，x2) x2 (x2，＋∞) f′(x) ＋ 0 － 0 ＋ f(x) 极大值 极小值 此时 f(x)在 0，a－ a2－8 2 上单调递增， 在 a－ a2－8 2 ，a＋ a2－8 2 上单调递减， 在 a＋ a2－8 2 ，＋∞ 上单调递增． 跟踪演练 2 求下列函数的单调区间： (1)f(x)＝(x－3)ex，x∈(0，＋∞)； (2)f(x)＝x(x－a)2. 解 (1)f′(x)＝(x－3)′ex＋(x－3)(ex)′＝(x－2)ex，令 f′(x)＞0，解得 x＞2，又 x∈(0，＋ ∞)， 所以函数的单调增区间(2，＋∞)，函数的单调减区间(0,2)． (2)函数 f(x)＝x(x－a)2＝x3－2ax2＋a2x 的定义域为 R， 由 f′(x)＝3x2－4ax＋a2＝0，得 x1＝a 3 ，x2＝a. ①当 a>0 时，x1x2， ∴函数 f(x)的单调递增区间为(－∞，a)， a 3 ，＋∞ ， 单调递减区间为 a，a 3 . ③当 a＝0 时，f′(x)＝3x2≥0，∴函数 f(x)的单调区间为(－∞，＋∞)，即 f(x)在 R 上是递增 的． 综上，a>0 时，函数 f(x)的单调递增区间为 －∞，a 3 ，(a，＋∞)，单调递减区间为 a 3 ，a . a<0 时，函数 f(x)的单调递增区间为(－∞，a)， a 3 ，＋∞ ，单调递减区间为 a，a 3 . a＝0 时，函数 f(x)的单调递增区间为(－∞，＋∞)． 题型三 利用导数求函数的极值和最值 1．利用导数求函数极值的一般步骤 (1)确定函数 f(x)的定义域； (2)解方程 f′(x)＝0 的根； (3)检验 f′(x)＝0 的根的两侧 f′(x)的符号． 若左正右负，则 f(x)在此根处取得极大值； 若左负右正，则 f(x)在此根处取得极小值； 否则，此根不是 f(x)的极值点． 2．求函数 f(x)在闭区间[a，b]上的最大值、最小值的方法与步骤 (1)求 f(x)在(a，b)内的极值； (2)将(1)求得的极值与 f(a)、f(b)相比较，其中最大的一个值为最大值，最小的一个值为最小 值． 特别地，①当 f(x)在[a，b]上单调时，其最小值、最大值在区间端点取得；②当 f(x)在(a，b) 内只有一个极值点时，若在这一点处 f(x)有极大(或极小)值，则可以断定 f(x)在该点处取得最 大(最小)值， 这里(a，b)也可以是(－∞，＋∞)． 例 3 已知函数 f(x)＝1 2x2－aln x(a∈R), (1)若 f(x)在 x＝2 时取得极值，求 a 的值； (2)求 f(x)的单调区间； (3)求证：当 x＞1 时，1 2x2＋ln x＜2 3x3. (1)解 f′(x)＝x－a x ，因为 x＝2 是一个极值点，所以 2－a 2 ＝0，则 a＝4.此时 f′(x)＝x－4 x ＝ x＋2x－2 x ，因为 f(x)的定义域是(0，＋∞)，所以当 x∈(0,2)时，f′(x)＜0；当 x∈(2，＋ ∞)，f′(x)＞0，所以当 a＝4 时，x＝2 是一个极小值点，故 a＝4. (2)解 因为 f′(x)＝x－a x ＝x2－a x ，所以当 a≤0 时，f(x)的单调递增区间为(0，＋∞)． 当 a＞0 时，f′(x)＝x－a x ＝x2－a x ＝x＋ ax－ a x ，所以函数 f(x)的单调递增区间( a，＋ ∞)；递减区间为(0， a)． (3)证明 设 g(x)＝2 3x3－1 2x2－ln x，则 g′(x)＝2x2－x－1 x ，因为当 x＞1 时，g′(x)＝ x－12x2＋x＋1 x ＞0，所以 g(x)在 x∈(1，＋∞)上是增函数，所以 g(x)＞g(1)＝1 6 ＞0，所以 当 x＞1 时，1 2x2＋ln x＜2 3x3. 跟踪演练 3 已知函数 f(x)＝x3＋ax2＋b 的图象上一点 P(1,0)，且在点 P 处的切线与直线 3x ＋y＝0 平行． (1)求函数 f(x)的解析式； (2)求函数 f(x)在区间[0，t](00.要使 g(x)＝0 在[1,3]上恰有两个相异的实 根，则 g1≥0， g2<0， g3≥0， 解得－20， f3≤0， 即 －1 3 ＋b≤0， b>0， －1＋b≤0， 解得 0