高中数学第一章解三角形1_1正弦定理和余弦定理1_1_1正弦定理课堂探究学案新人教B版必修51 6页

1.1.1 正弦定理 课堂探究 一、判断三角形解的个数 剖析：(1)代数法 在△ABC 中，已知 a，b，∠A，由正弦定理可得 sin B＝ b a sin A＝m． ①当 sin B>1 时，这样的∠B不存在，即三角形无解． ②当 sin B＝1 时，∠B＝90°，若∠A<90°，则三角形有一解，否则无解． ③当 sin B<1 时，满足 sin B＝m 的角有两个，其中设锐角为α，钝角为β，则当∠A ＋α>180°时，三角形无解；当∠A＋α<180°，且∠A＋β<180°时，有两解；当∠A＋ α<180°且∠A＋β>180°时有一解． (2)几何法 根据条件中∠A 的大小，分为锐角、直角、钝角三种情况，通过几何作图，得出解的情 况．作出已知∠A，以 A为圆心，边长 b为半径画弧交∠A 的一边于 C．使未知的边 AB 水平， 顶点 C在边 AB 上方，以点 C 为圆心，边长 a 为半径作圆，该圆与射线 AB 交点的个数，即为 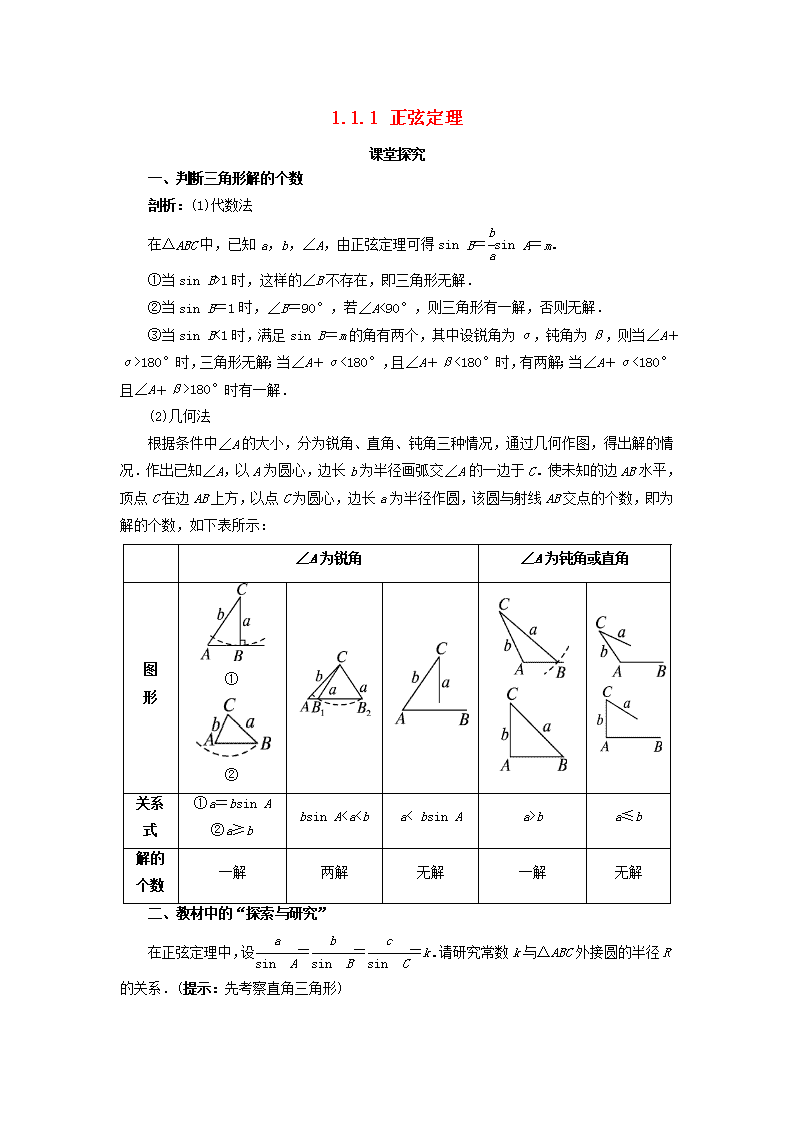解的个数，如下表所示： ∠A 为锐角 ∠A 为钝角或直角 图 形 ① ② 关系 式 ①a＝bsin A ②a≥b bsin Ab a≤b 解的 个数 一解 两解 无解 一解 无解 二、教材中的“探索与研究” 在正弦定理中，设 a sin A ＝ b sin B ＝ c sin C ＝k．请研究常数 k 与△ABC 外接圆的半径 R 的 关系．(提示：先考察直角三角形) 剖析：(1)如图 1，当△ABC 为直角三角形时，直接得到 a sin A ＝ b sin B ＝ c sin C ＝2R(a，b， c分别为△ABC 中角 A，B，C 的对边，R为外接圆半径)． (2)如图 2，当△ABC 为锐角三角形时，连接 BO 并延长交圆 O于点 D，连接 CD．因为∠A ＝∠D， 所以 a sin A ＝ a sin D ＝2R， 同理 b sin B ＝ c sin C ＝2R， 即 a sin A ＝ b sin B ＝ c sin C ＝2R． (3)如图 3，当△ABC 为钝角三角形且∠A 为钝角时，连接 BO 并延长交圆 O于点 D，连接 CD，∠A＝180°－∠D，所以 a sin A ＝ a sin(180°－∠D) ＝ a sin D ＝2R． 由(2)知 b sin B ＝ c sin C ＝2R， 即 a sin A ＝ b sin B ＝ c sin C ＝2R． 综上所述，对于任意△ABC， a sin A ＝ b sin B ＝ c sin C ＝2R 恒成立． 归纳总结：根据上述关系式可得到正弦定理的常用变式： (1)asin B＝bsin A；asin C＝csin A；bsin C＝csin B． (2)a＝ bsin A sin B ；sin B＝ bsin A a ． (3) a sin A ＝ b sin B ＝ c sin C ＝ a＋b＋c sin A＋sin B＋sin C ＝2R(R 为△ABC 外接圆的半径)． (4)a∶b∶c＝sin A∶sin B∶sin C． (5)边化角公式：a＝2Rsin A，b＝2Rsin B，c＝2Rsin C． (6)角化边公式：sin A＝ a 2R ，sin B＝ b 2R ，sin C＝ c 2R ． 题型一 解三角形 【例 1】 已知在△ABC 中，c＝10，∠A＝45°，∠C＝30°，求 a，b 和∠B． 分析：正弦定理中有三个等式，每个等式都含有四个未知量，可知三求一．当知道两个 角时，即可知道第三个角，所以若再知道三边中任意一边，就可解这个三角形． 解：∵ a sin A ＝ c sin C ，∠A＝45°，∠C＝30°， ∴a＝ csin A sin C ＝ 10×sin 45° sin 30° ＝10 2， ∠B＝180°－(∠A＋∠C)＝180°－(45°＋30°)＝105°． 又 b sin B ＝ c sin C ， ∴b＝ c·sin B sin C ＝ 10×sin 105° sin 30° ＝20sin 75°＝20× 6＋ 2 4 ＝5( 6＋ 2)． 反思：本题给出了解三角形第一类问题(即已知两角和一边，求另两边和一角)的方法步 骤，即先由正弦定理求得已知角的对边，然后利用内角和公式求得第三角，再用正弦定理求 第三边． 【例 2】 在△ABC 中，已知 a＝ 3，b＝ 2，∠B＝45°，求∠A，∠C和 c． 分析：已知两边和其中一边的对角的解三角形问题可运用正弦定理来求解，但应注意解 的个数． 解：由正弦定理 a sin A ＝ b sin B ，知 sin A＝ asin B b ＝ 3 2 ． ∵asin BAC，得满足 sin C＝ 3 2 的角 C 有两个． 正解：由正弦定理，得 sin C＝ ABsin B AC ＝ 3 2 ． 因为 AB>AC，所以∠C＝60°或 120°． 当∠C＝60°时，∠A＝90°，S△ABC＝ 1 2 AB·AC·sin A＝2 3；当∠C＝120°时，∠A ＝30°，S△ABC＝ 1 2 AB·AC·sin A＝ 3．所以△ABC 的面积为 2 3或 3． 【例 6】 在△ABC 中，角 A，B，C 的对边分别为 a，b，c，c＝ 6＋ 2，∠C＝30°，求 a ＋b 的最大值． 错解：因为∠C＝30°，所以∠A＋∠B＝150°， 即∠B＝150°－∠A． 由正弦定理，得 a sin A ＝ b sin(150°－∠A) ＝ 6＋ 2 sin 30° ． 又因为 sin A≤1，sin(150°－∠A)≤1， 所以 a＋b≤2( 6＋ 2)＋2( 6＋ 2)＝4( 6＋ 2)． 故 a＋b的最大值为 4( 6＋ 2)． 错因分析：上述解法错误的原因是未弄清∠A 与 150°－∠A 之间的关系，这里∠A 与 150°－∠A 是相互制约的，不是相互独立的量，sin A 与 sin(150°－∠A)不能同时取 最大值 1，因此所得的结果是错误的． 正解：因为 C＝30°，所以∠A＋∠B＝150°． 由正弦定理，得 a sin A ＝ b sin(150°－∠A) ＝ 6＋ 2 sin 30° ． 因此，a＋b＝2( 6＋ 2)·[sin A＋sin(150°－∠A)] ＝(8＋4 3)cos(∠A－75°)≤8＋4 3． 故 a＋b 的最大值为 8＋4 3．