2020-2021学年数学新教材人教B版必修第四册课时分层作业：10 6页

www.ks5u.com 课时分层作业(六)　复数的加法与减法 ‎(建议用时：40分钟)‎ 一、选择题 ‎1．如图，在复平面内，复数z1，z2对应的向量分别是，，则复数z1－z2＝(　　)‎ A．－1＋2i B．－2－2i C．1＋2i D．1－2i B　[由题意知z1＝－2－i，z2＝i，所以z1－z2＝－2－2i，故选B．]‎ ‎2．设z1＝3－4i，z2＝－2＋3i，则z1－z2在复平面内对应的点位于(　　)‎ A．第一象限 B．第二象限 ‎ C．第三象限 D．第四象限 D　[z1－z2＝(3－4i)－(－2＋3i)＝5－7i，在复平面内z1－z2对应点的坐标为(5，－7)，位于第四象限．]‎ ‎3．已知复数z＝a＋i(a∈R)，若z＋＝4，则复数z的共轭复数＝(　　)‎ A．2＋i B．2－i C．－2＋i D．－2－i B　[∵z＝a＋i，‎ ‎∴z＋＝‎2a＝4，得a＝2.‎ ‎∴复数z的共轭复数＝2－i.‎ 故选B．]‎ ‎4．复平面内正方形三个顶点分别对应复数z1＝1＋2i，z2＝－2＋i，z3＝－1－2i，则另一个顶点对应的复数为(　　)‎ A．2－i B．5i C．－4－3i D．2－i,5i或－4－3i A　[如图所示，利用＝，或者＝，求另一顶点对应的复数．设复数z1，z2，z3对应的点分别为A，B，C，正方形的第四个顶点D对应的复数为x＋yi(x，y∈R)，则＝－＝(x＋yi)－(1＋2i)＝(x－1)＋(y－2)i，＝－＝(－1－2i)－(－2＋i)＝1－3i.‎ ‎∵＝，∴(x－1)＋(y－2)i＝1－3i，‎ ‎∴解得 故D点对应的复数为2－i.]‎ ‎5．A，B分别是复数z1，z2在复平面内对应的点，O是原点，若|z1＋z2|＝|z1－z2|，则三角形AOB一定是(　　)‎ A．等腰三角形 B．直角三角形 C．等边三角形 D．等腰直角三角形 B　[复数z1对应向量，复数z2对应向量.‎ 则|z1＋z2|＝|＋|，|z1－z2|＝|O－|，‎ 依题意有|＋|＝|－|.‎ ‎∴以，为邻边所作的平行四边形是矩形．‎ ‎∴△AOB是直角三角形．]‎ 二、填空题 ‎6．(一题两空)已知z1＝(3x＋y)＋(y－4x)i(x，y∈R)，z2＝(4y－2x)－(5x＋3y)i(x，y∈R)．设z＝z1－z2，且z＝13－2i，则z1＝__________，z2＝__________.‎ ‎5－9i　－8－7i　[z＝z1－z2‎ ‎＝－ ‎＝(5x－3y)＋(x＋4y)i＝13－2i，‎ ‎∴解得 ‎∴z1＝5－9i，z2＝－8－7i.]‎ ‎7．计算：(i2＋i)＋|－i|＋(i－2)＝________.‎ ‎－1＋2i　[(i2＋i)＋|－i|＋(i－2)‎ ‎＝(－1＋i)＋＋(－2＋i)‎ ‎＝－1＋i＋2－2＋i ‎＝－1＋2i.]‎ ‎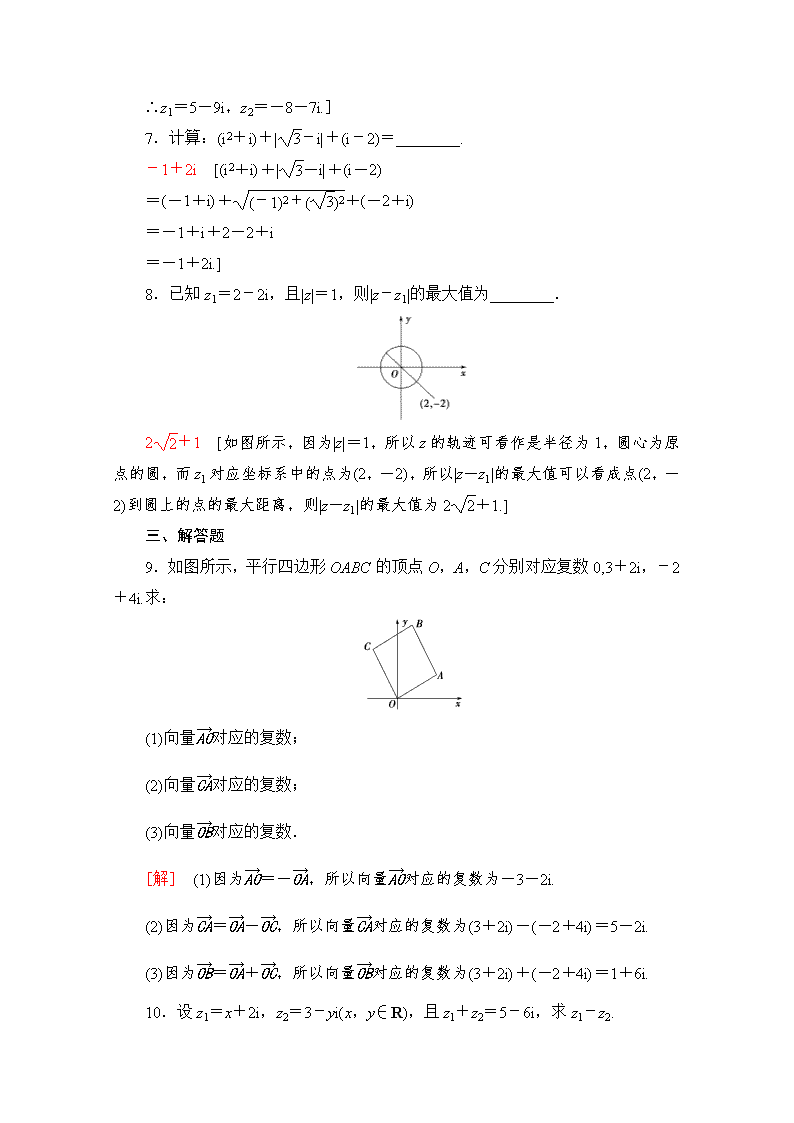8．已知z1＝2－2i，且|z|＝1，则|z－z1|的最大值为________．‎ ‎2＋1　[如图所示，因为|z|＝1，所以z的轨迹可看作是半径为1，圆心为原点的圆，而z1对应坐标系中的点为(2，－2)，所以|z－z1|的最大值可以看成点(2，－2)到圆上的点的最大距离，则|z－z1|的最大值为2＋1.]‎ 三、解答题 ‎9．如图所示，平行四边形OABC的顶点O，A，C分别对应复数0,3＋2i，－2＋4i.求：‎ ‎(1)向量对应的复数；‎ ‎(2)向量对应的复数；‎ ‎(3)向量对应的复数．‎ ‎[解]　(1)因为＝－，所以向量对应的复数为－3－2i.‎ ‎(2)因为＝－，所以向量对应的复数为(3＋2i)－(－2＋4i)＝5－2i.‎ ‎(3)因为＝＋，所以向量对应的复数为(3＋2i)＋(－2＋4i)＝1＋6i.‎ ‎10．设z1＝x＋2i，z2＝3－yi(x，y∈R)，且z1＋z2＝5－6i，求z1－z2.‎ ‎[解]　∵z1＝x＋2i，z2＝3－yi，‎ ‎∴z1＋z2＝x＋3＋(2－y)i＝5－6i，‎ ‎∴解得 ‎∴z1＝2＋2i，z2＝3－8i，‎ ‎∴z1－z2＝(2＋2i)－(3－8i)＝－1＋10i.‎ ‎11．(多选题)|(3＋2i)－(1＋i)|可表示(　　)‎ A．点(3,2)与点(1,1)之间的距离 B．点(3,2)与点(－1，－1)之间的距离 C．点(2,1)到原点的距离 D．点(2,2)到原点的距离 AC　[由复数的几何意义，知复数3＋2i,1＋i分别对应复平面内的点(3,2)与点(1,1)，所以|(3＋2i)－(1＋i)|表示点(3,2)与点(1,1)之间的距离，故A正确，B错误；(3＋2i)－(1＋i)＝2＋i，对应复平面内的点(2,1)，所以|(3＋2i)－(1＋i)|＝|2＋i|可表示点(2,1)到原点的距离，故C正确，D错误．]‎ ‎12．复数z＝x＋yi(x，y∈R)满足条件|z－4i|＝|z＋2|，则2x＋4y的最小值为(　　)‎ A．2 B．‎4 C．4 D．16‎ C　[由|z－4i|＝|z＋2|，得 ‎|x＋(y－4)i|＝|x＋2＋yi|，‎ ‎∴x2＋(y－4)2＝(x＋2)2＋y2，‎ 即x＋2y＝3，‎ ‎∴2x＋4y＝2x＋22y≥2＝2＝4，‎ 当且仅当x＝2y＝时，2x＋4y取得最小值4.]‎ ‎13．设f(z)＝z－3i＋|z|，若z1＝－2＋4i，z2＝5－i，则f(z1＋z2)＝__________.‎ ‎3＋3　[∵z1＋z2＝－2＋4i＋5－i＝3＋3i，‎ ‎∴f(z1＋z2)＝(3＋3i)－3i＋|3＋3i|‎ ‎＝3＋＝3＋3.]‎ ‎14．已知复数z1＝cos α＋isin α，z2＝cos β＋isin β，|z1－z2|＝，则cos(α－β ‎)＝________.‎ 　[因为z1＝cos α＋isin α，z2＝cos β＋isin β，‎ 所以z1－z2＝(cos α－cos β)＋i(sin α－sin β)．‎ 因为|z1－z2|＝，‎ 所以＝，‎ 两边平方后整理得cos(α－β)＝.]‎ ‎15．已知在复平面内，O为坐标原点，向量，分别对应复数z1，z2，且z1＝＋(10－a2)i，z2＝＋(‎2a－5)i，＋z2是实数．‎ ‎(1)求实数a的值；‎ ‎(2)求以，为邻边的平行四边形的面积S.‎ ‎[解]　(1)∵＋z2＝－(10－a2)i＋＋(‎2a－5)i＝＋(a2＋‎2a－15)i是实数，‎ ‎∴a2＋‎2a－15＝0，∴a＝3或a＝－5(舍去)，∴a＝3.‎ ‎(2)由(1)知z1＝＋i，z2＝－1＋i，‎ ‎∴＝，＝(－1,1)，‎ ‎∴||＝，||＝，‎ ‎∴cos〈，〉＝＝＝，‎ ‎∴sin〈，〉＝＝，‎ ‎∴S＝||||sin〈，〉＝××＝.‎