2008年安徽省高考数学试卷（理科）【附答案、word版本，可再编辑；B4纸型两栏】 7页

1 / 7 2008 年安徽省高考数学试卷（理科） 一、选择题（共 12 小题，每小题 5 分，满分 60 分） 1. 复数푖3(1 + 푖)2＝（ ） A.2 B. ― 2 C.2푖 D. ― 2푖 2. 集合퐴 = {푦 ∈ R|푦 = lg푥, 푥 > 1}，퐵 = { ― 2,  ― 1, 1, 2}，则下列结论正确的是 （ ） A.퐴 ∩ 퐵 = { ― 2,  ― 1} B.(∁R퐴) ∪ 퐵 = ( ― ∞, 0) C.퐴 ∪ 퐵 = (0,  + ∞) D.(∁R퐴) ∩ 퐵 = { ― 2,  ― 1} 3. 在平行四边形퐴퐵퐶퐷中，퐴퐶为一条对角线，若 → 퐴퐵 = (2,4)， → 퐴퐶 = (1,3)，则 → 퐵퐷 = ( ) A.( ― 2,  ― 4) B.( ― 3,  ― 5) C.(3, 5) D.(2, 4) 4. 푚，푛是两条不同直线，훼，훽，훾是三个不同平面，下列命题中正确的是（ ） A.若푚 // ∂，푛 // ∂，则푚 // 푛 B.若훼 ⊥ 훾，훽 ⊥ 훾，则훼 // 훽 C.若푚 // 훼，푚 // 훽，则훼 // 훽 D.若푚 ⊥ 훼，푛 ⊥ 훼，则푚 // 푛 5. 将函数푦 = sin(2푥 + 휋 3)的图象按向量 → 푎平移后所得的图象关于点( ― 휋 12，0)中心对 称，则向量훼的坐标可能为（ ） A.( ― 휋 12，0) B.( ― 휋 6，0) C.( 휋 12，0) D.(휋 6，0) 6. 设(1 + 푥)8 = 푎0 + 푎1푥 +... + 푎8푥8，则푎0，푎1，…，푎8中奇数的个数为 （ ） A.2 B.3 C.4 D.5 7. 푎 < 0是方程푎푥2 +2푥 +1 = 0至少有一个负数根的（ ） A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要条件 8. 若过点퐴(4, 0)的直线푙与曲线(푥 ― 2)2 + 푦2 = 1有公共点，则直线푙的斜率的取值范 围为（ ） A. [ ― 3， 3] B.( ― 3， 3) C. [ ― 3 3 ， 3 3 ] D.( ― 3 3 ， 3 3 ) 9. 在同一平面直角坐标系中，函数푦＝푔(푥)的图象与푦＝푒푥的图象关于直线푦＝푥对 称．而函数푦＝푓(푥)的图象与푦＝푔(푥)的图象关于푦轴对称，若푓(푚)＝ ― 1，则푚的值是 （ ） A. ― 푒 B. ― 1 푒 C.푒 D.1 푒 10. 设两个正态分布푁(휇1, 휎21)(휎1 > 0)和푁(휇2, 휎22)(휎2 > 0)曲线如图所示，则有（ ） A.휇1 < 휇2，휎1 > 휎2 B.휇1 < 휇2，휎1 < 휎2 C.휇1 > 휇2，휎1 > 휎2 D.휇1 > 휇2， 휎1 < 휎2 11. 若函数푓(푥)，푔(푥)分别是푅上的奇函数、偶函数，且满足푓(푥) ― 푔(푥)＝푒푥，则有 （ ） A.푓(2) < 푓(3) < 푔(0) B.푔(0) < 푓(3) < 푓(2) C.푓(2) < 푔(0) < 푓(3) D.푔(0) < 푓(2) < 푓(3) 12. 12名同学合影，站成前排4人后排8人，现摄影师要从后排8人中抽2人调整到前 排，若其他人的相对顺序不变，则不同调整方法的总数是（ ） A.퐶28퐴23 B.퐶28퐴66 C.퐶28퐴26 D.퐶28퐴25 二、填空题（共 4 小题，每小题 4 分，满分 16 分） 13. 函数푓(푥) = |푥 ― 2| ― 1 log2(푥 ― 1) 的定义域为________． 14. 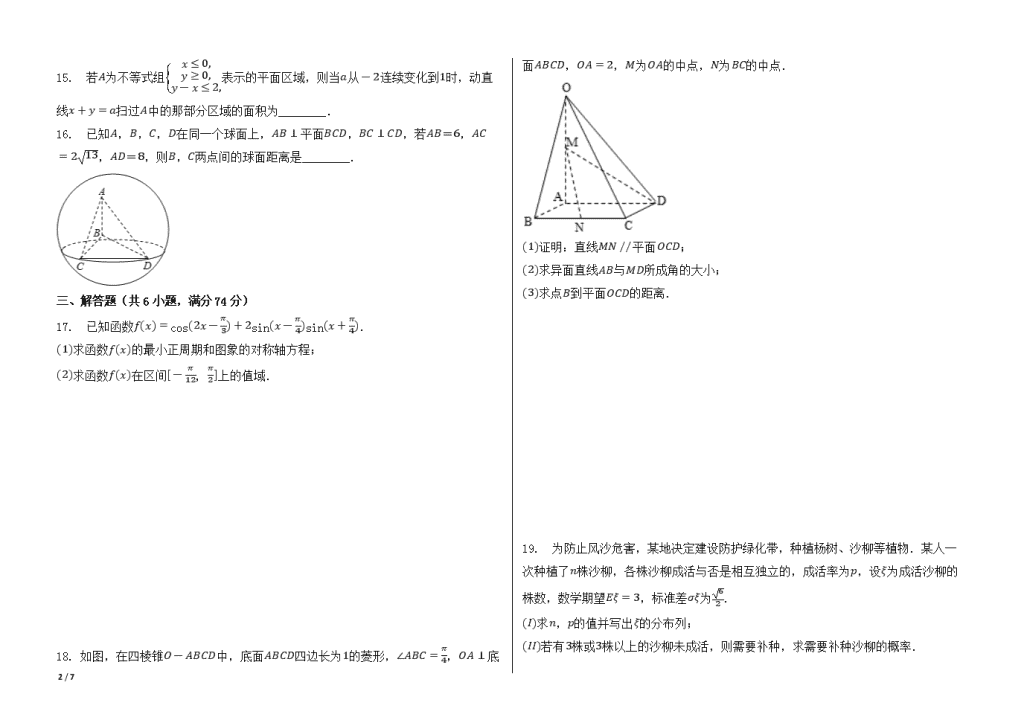在数列{푎푛}中，푎푛 = 4푛 ― 5 2，푎1 + 푎2 +...푎푛 = 푎푛2 + 푏푛，푛 ∈ 푁∗，其中푎，푏为常 数，则 lim 푛→∞ 푎푛 ― 푏푛 푎푛 + 푏푛的值是________． 2 / 7 15. 若퐴为不等式组{ 푥 ≤ 0, 푦 ≥ 0, 푦 ― 푥 ≤ 2, 表示的平面区域，则当푎从 ― 2连续变化到1时，动直 线푥 + 푦 = 푎扫过퐴中的那部分区域的面积为________． 16. 已知퐴，퐵，퐶，퐷在同一个球面上，퐴퐵 ⊥ 平面퐵퐶퐷，퐵퐶 ⊥ 퐶퐷，若퐴퐵＝6，퐴퐶 = 2 13，퐴퐷＝8，则퐵，퐶两点间的球面距离是________． 三、解答题（共 6 小题，满分 74 分） 17. 已知函数푓(푥) = cos(2푥 ― 휋 3) + 2sin(푥 ― 휋 4)sin(푥 + 휋 4)． (1)求函数푓(푥)的最小正周期和图象的对称轴方程； (2)求函数푓(푥)在区间[ ― 휋 12，휋 2]上的值域． 18. 如图，在四棱锥푂 ― 퐴퐵퐶퐷中，底面퐴퐵퐶퐷四边长为1的菱形，∠퐴퐵퐶 = 휋 4，푂퐴 ⊥ 底 面퐴퐵퐶퐷，푂퐴 = 2，푀为푂퐴的中点，푁为퐵퐶的中点． (1)证明：直线푀푁 // 平面푂퐶퐷； (2)求异面直线퐴퐵与푀퐷所成角的大小； (3)求点퐵到平面푂퐶퐷的距离． 19. 为防止风沙危害，某地决定建设防护绿化带，种植杨树、沙柳等植物．某人一 次种植了푛株沙柳，各株沙柳成活与否是相互独立的，成活率为푝，设휉为成活沙柳的 株数，数学期望퐸휉 = 3，标准差휎휉为 6 2 ． (퐼)求푛，푝的值并写出휉的分布列； 3 / 7 (퐼퐼)若有3株或3株以上的沙柳未成活，则需要补种，求需要补种沙柳的概率． 20. 设函数푓(푥) = 1 푥ln푥(푥 > 0且푥 ≠ 1)． (1)求函数푓(푥)的单调区间； (2)已知2 1 푥 > 푥푎对任意푥 ∈ (0, 1)成立，求实数푎的取值范围． 21. 设数列{푎푛}满足푎1 = 0，푎푛+1 = 푐푎3푛 +1 ― 푐，푛 ∈ 푁∗，其中푐为实数 （1）证明：푎푛 ∈ [0, 1]对任意푛 ∈ 푁∗成立的充分必要条件是푐 ∈ [0, 1]； （2）设0 < 푐 < 1 3，证明：푎푛 ≥ 1 ― (3푐)푛―1，푛 ∈ 푁∗； （3）设0 < 푐 < 1 3，证明：푎21 + 푎22 +…푎2푛 > 푛 +1 ― 2 1 ― 3푐，푛 ∈ 푁∗． 22. 设椭圆퐶：푥2 푎2 + 푦2 푏2 = 1(푎 > 푏 > 0)过点푀( 2，1)，且左焦点为퐹1( ― 2,0) （1）求椭圆퐶的方程； （2）当过点푃(4, 1)的动直线푙与椭圆퐶相交于两不同点퐴，퐵时，在线段퐴퐵上取点푄， 满足| → 퐴푃| ⋅ | → 푄퐵| = | → 퐴푄| ⋅ | → 푃퐵|，证明：点푄总在某定直线上． 4 / 7 参考答案与试题解析 2008 年安徽省高考数学试卷（理科） 一、选择题（共 12 小题，每小题 5 分，满分 60 分） 1.A 2.D 3.B 4.D 5.C 6.A 7.B 8.C 9.B 10.A 11.D 12.C 二、填空题（共 4 小题，每小题 4 分，满分 16 分） 13.{푥|푥 ≥ 3} 14.1 15.7 4 16.4휋 3 三、解答题（共 6 小题，满分 74 分） 17.解：(1)∵ 푓(푥) = cos(2푥 ― 휋 3) + 2sin(푥 ― 휋 4)sin(푥 + 휋 4) = 1 2cos2푥 + 3 2 sin2푥 + (sin푥 ― cos푥)(sin푥 + cos푥) = 1 2cos2푥 + 3 2 sin2푥 + sin2푥 ― cos2푥 = 1 2cos2푥 + 3 2 sin2푥 ― cos2푥 = sin(2푥 ― 휋 6)， ∴ 周期푇 = 2휋 2 = 휋. 由2푥 ― 휋 6 = 푘휋 + 휋 2(푘 ∈ 퐙)，得푥 = 푘휋 2 + 휋 3(푘 ∈ 퐙)， ∴ 函数图象的对称轴方程为푥 = 푘휋 2 + 휋 3(푘 ∈ 퐙). (2)∵ 푥 ∈ [ ― 휋 12，휋 2]，∴ 2푥 ― 휋 6 ∈ [ ― 휋 3,5휋 6 ]， 因为푓(푥) = sin(2푥 ― 휋 6)在区间[ ― 휋 12，휋 3]上单调递增，在区间[휋 3，휋 2]上单调递减， 所以当푥 = 휋 3时，푓(푥)取最大值1， 又∵ 푓( ― 휋 12) = ― 3 2 < 푓(휋 2) = 1 2，当푥 = ― 휋 12时，푓(푥)取最小值 ― 3 2 ， 所以函数푓(푥)在区间[ ― 휋 12，휋 2]上的值域为[ ― 3 2 ，1]． 18.(1)证明：取푂퐵中点퐸，连结푀퐸，푁퐸， ∵ 푀퐸 // 퐴퐵，퐴퐵 // 퐶퐷， ∴ 푀퐸 // 퐶퐷， 又∵ 푁퐸 // 푂퐶， ∴ 平面푀푁퐸 // 平面푂퐶퐷， ∴ 푀푁 // 平面푂퐶퐷. 5 / 7 (2)解：∵ 퐶퐷 // 퐴퐵， ∴ ∠푀퐷퐶为异面直线퐴퐵与푀퐷所成的角（或其补角）， 作퐴푃 ⊥ 퐶퐷于푃，连结푀푃， ∵ 푂퐴 ⊥ 平面퐴퐵퐶퐷， ∴ 퐶퐷 ⊥ 푀푃， ∵ ∠퐴퐷푃 = 휋 4， ∴ 퐷푃 = 2 2 ，푀퐷 = 푀퐴2 + 퐴퐷2 = 2， ∴ cos∠푀퐷푃 = 퐷푃 푀퐷 = 1 2，∠푀퐷퐶 = ∠푀퐷푃 = 휋 3， ∴ 퐴퐵与푀퐷所成角的大小为휋 3． (3)解：∵ 퐴퐵 // 平面푂퐶퐷， ∴ 点퐴和点퐵到平面푂퐶퐷的距离相等，连结푂푃，过点퐴作퐴푄 ⊥ 푂푃于点푄， ∵ 퐴푃 ⊥ 퐶퐷，푂퐴 ⊥ 퐶퐷， ∴ 퐶퐷 ⊥ 平面푂퐴푃， ∴ 퐴푄 ⊥ 퐶퐷． 又∵ 퐴푄 ⊥ 푂푃， ∴ 퐴푄 ⊥ 平面푂퐶퐷，线段퐴푄的长就是点퐴到平面푂퐶퐷的距离， ∵ 푂푃 = 푂퐷2 ― 퐷푃2 = 푂퐴2 + 퐴퐷2 ― 퐷푃2 = 4 + 1 ― 1 2 = 3 2 2 ， 퐴푃 = 퐷푃 = 2 2 ， ∴ 퐴푄 = 푂퐴 ⋅ 퐴푃 푂푃 = 2 × 2 2 3 2 2 = 2 3， ∴ 点퐵到平面푂퐶퐷的距离为2 3． 19.解：(1)由题意知本题符合二项分布，根据二项分布的期望和方差公式得到， 퐸휉 = 푛푝 = 3，(휎휉)2 = 푛푝(1 ― 푝) = 3 2， 得1 ― 푝 = 1 2， 从而푛 = 6，푝 = 1 2 ∴ 휉的分布列为 휉 0 1 2 3 4 5 6 6 / 7 푃 1 64 6 64 15 64 20 64 15 64 6 64 1 64 (2)记”需要补种沙柳”为事件퐴， 则푃(퐴) = 푃(휉 ≥ 3)， 得푃(퐴) = 1 + 6 + 15 + 20 64 = 21 32， 20.解：(1)푓′(푥) = ― ln푥 + 1 푥2ln2푥 ，若푓′(푥) = 0，则푥 = 1 푒， 列表如下 ： 푥 (0, 1 푒) 1 푒 ( 1 푒，1) (1,  + ∞) 푓′(푥) + 0 - - 푓(푥) 单调递增 极大值푓(1 푒) 单调递减 单调递减 ∴ 푓(푥)的单调递增区间为：(0,1 푒)；单调递减区间为(1 푒，1)，(1,  + ∞)； (2)在2 1 푥 > 푥푎两边取对数，得1 푥ln2 > 푎ln푥， 由于0 < 푥 < 1，∴ ln푥 < 0，∴ 푎 ln2 > 1 푥ln푥①， 由(1)的结果可知，当푥 ∈ (0, 1)时，푓(푥) ≤ 푓(1 푒) = ― 푒， ∵ ①式对所有푥 ∈ (0, 1)成立， ∴ 푎 ln2 > ― 푒，即푎 > ― 푒ln2. 21.解：（1）必要性：∵ 푎1 = 0，∴ 푎2 = 1 ― 푐， 又∵ 푎2 ∈ [0, 1]，∴ 0 ≤ 1 ― 푐 ≤ 1，即푐 ∈ [0, 1] 充分性：设푐 ∈ [0, 1]，对푛 ∈ 푁∗用数学归纳法证明푎푛 ∈ [0, 1] 当푛 = 1时，푎1 = 0 ∈ [0, 1]．假设푎푘 ∈ [0, 1](푘 ≥ 1) 则푎푘+1 = 푐푎3푘 +1 ― 푐 ≤ 푐 +1 ― 푐 = 1，且푎푘+1 = 푐푎3푘 +1 ― 푐 ≥ 1 ― 푐 =≥ 0 ∴ 푎푘+1 ∈ [0, 1]，由数学归纳法知푎푛 ∈ [0, 1]对所有푛 ∈ 푁∗成立 （2）设0 < 푐 < 1 3，当푛 = 1时，푎1 = 0，结论成立， 当푛 ≥ 2时，∵ 푎푛 = 푐푎3푛―1 +1 ― 푐， ∴ 1 ― 푎푛 = 푐(1 ― 푎푛―1)(1 + 푎푛―1 + 푎2푛―1) ∵ 0 < 퐶 < 1 3，由（1）知푎푛―1 ∈ [0, 1]，所以1 + 푎푛―1 + 푎2푛―1 ≤ 3且1 ― 푎푛―1 ≥ 0 ∴ 1 ― 푎푛 ≤ 3푐(1 ― 푎푛―1) ∴ 1 ― 푎푛 ≤ 3푐(1 ― 푎푛―1) ≤ (3푐)2(1 ― 푎푛―2) ≤≤ (3푐)푛―1(1 ― 푎1) = (3푐)푛―1 ∴ 푎푛 ≥ 1 ― (3푐)푛―1(푛 ∈ 푁∗) （3）设0 < 푐 < 1 3，当푛 = 1时，푎21 = 0 > 2 ― 2 1 ― 3푐，结论成立 当푛 ≥ 2时，由（2）知푎푛 ≥ 1 ― (3푐)푛―1 > 0 ∴ 푎2푛 ≥ (1 ― (3푐)푛―1)2 = 1 ― 2(3푐)푛―1 +(3푐)2（푛―1） > 1 ― 2(3푐)푛―1 ∴ 푎21 + 푎22 +... + 푎2푛 = 푎22 +... + 푎2푛 > 푛 ― 1 ― 2[3푐 +(3푐)2 +... + (3푐)푛―1] = 푛 ― 1 ― 2 × 3푐[1 ― (3푐)푛―1] 1 ― 3푐 = 푛 ― 1 ― 2 × 3푐 ― (3푐)푛 1 ― 3푐 = 푛 + 1 ― 2(1 ― (3푐)푛) 1 ― 3푐 > 푛 + 1 ― 2 1 ― 3푐 22.解：（1）由题意得{ 푐2 = 2 2 푎2 + 1 푏2 = 1 푐2 = 푎2 ― 푏2 ， 解得푎2 = 4，푏2 = 2， 所以椭圆퐶的方程为푥2 4 + 푦2 2 = 1． （2）设点푄、퐴、퐵的坐标分别为(푥, 푦)，(푥1, 푦1)，(푥2, 푦2)． 由题设知| → 퐴푃|，| → 푃퐵|，| → 퐴푄|，| → 푄퐵|均不为零，记휆 = | → 퐴푃| | → 푃퐵| = | → 퐴푄| | → 푄퐵| ，则휆 > 0且휆 ≠ 1 又퐴，푃，퐵，푄四点共线，从而 → 퐴푃 = ― 휆 → 푃퐵， → 퐴푄 = 휆 → 푄퐵 于是4 = 푥1 ― 휆푥2 1 ― 휆 ，1 = 푦1 ― 휆푦2 1 ― 휆 ，푥 = 푥1 + 휆푥2 1 + 휆 ，푦 = 푦1 + 휆푦2 1 + 휆 7 / 7 从而푥21 ― 휆2푥22 1 ― 휆2 = 4푥①，푦21 ― 휆2푦22 1 ― 휆2 = 푦②， 又点퐴、퐵在椭圆퐶上，即푥21 +2푦21 = 4 ③，푥22 +2푦22 = 4 ④， ①+② × 2并结合③、④得4푥 +2푦 = 4， 即点푄(푥, 푦)总在定直线2푥 + 푦 ― 2 = 0上．