2020学年度高中数学 第二章 基本初等函数（Ⅰ）检测试题 新人教A版必修1 7页

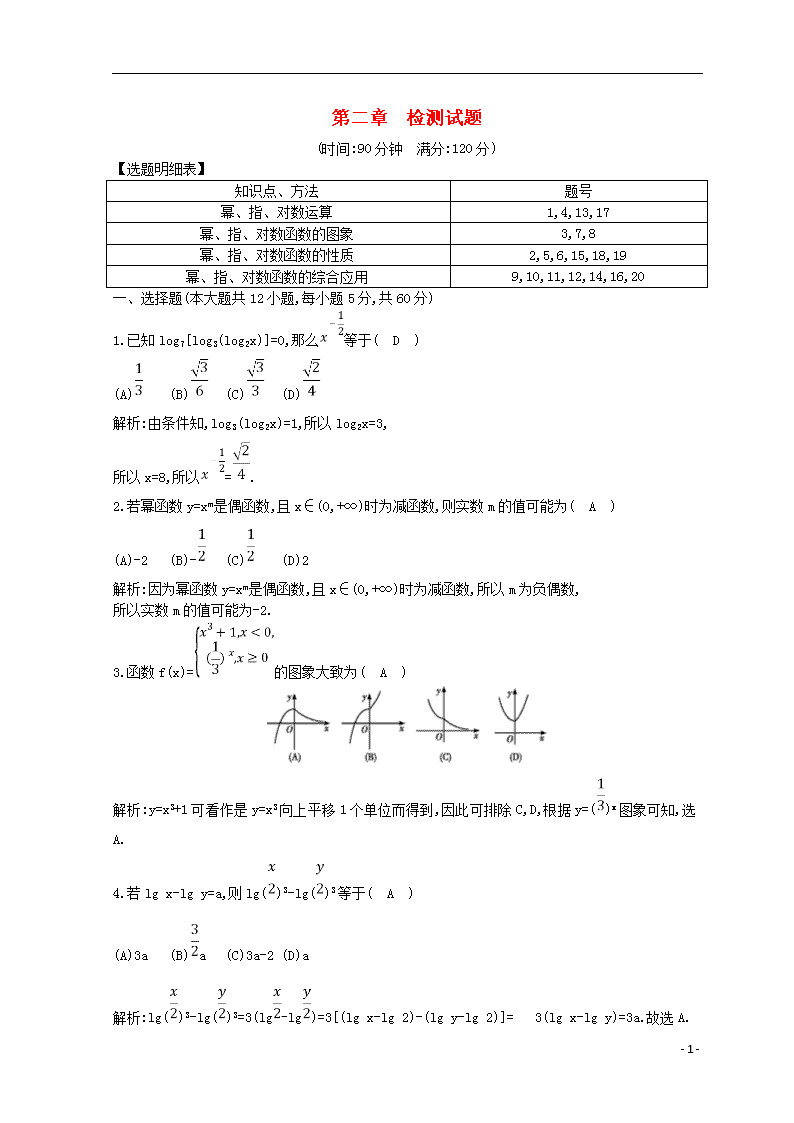
第二章　检测试题 ‎(时间:90分钟　满分:120分)‎ ‎【选题明细表】‎ 知识点、方法 题号 幂、指、对数运算 ‎1,4,13,17‎ 幂、指、对数函数的图象 ‎3,7,8‎ 幂、指、对数函数的性质 ‎2,5,6,15,18,19‎ 幂、指、对数函数的综合应用 ‎9,10,11,12,14,16,20‎ 一、选择题(本大题共12小题,每小题5分,共60分)‎ ‎1.已知log7[log3(log2x)]=0,那么等于(　D　)‎ ‎(A) (B) (C) (D)‎ 解析:由条件知,log3(log2x)=1,所以log2x=3,‎ 所以x=8,所以=.‎ ‎2.若幂函数y=xm是偶函数,且x∈(0,+∞)时为减函数,则实数m的值可能为(　A　)‎ ‎(A)-2 (B)- (C) (D)2‎ 解析:因为幂函数y=xm是偶函数,且x∈(0,+∞)时为减函数,所以m为负偶数,‎ 所以实数m的值可能为-2.‎ ‎3.函数f(x)=的图象大致为(　A　)‎ 解析:y=x3+1可看作是y=x3向上平移1个单位而得到,因此可排除C,D,根据y=()x图象可知,选A.‎ ‎4.若lg x-lg y=a,则lg()3-lg()3等于(　A　)‎ ‎(A)‎3a (B)a (C)‎3a-2 (D)a 解析:lg()3-lg()3=3(lg-lg)=3[(lg x-lg 2)-(lg y-lg 2)]= 3(lg x-lg y)=‎3a.故选A.‎ - 7 -‎ ‎5.若a=log36,b=log612,c=log816,则(　D　)‎ ‎(A)c>b>a (B)b>c>a ‎(C)a>c>b (D)a>b>c 解析:a=log36=1+log32,b=log612=1+log62,‎ c=log816=1+log82.‎ 因为y=log2x是增函数,‎ 所以log28>log26>log23>log22=1,‎ 所以log32>log62>log82,所以a>b>c.‎ ‎6.若函数f(x)=是R上的增函数,则实数a的取值范围为(　D　)‎ ‎(A)(1,+∞) (B)(1,8)‎ ‎(C)(4,8) (D)[4,8)‎ 解析:由题意得 解得4≤a<8.故选D.‎ ‎7.若函数y=ax+b(a>0且a≠1)的图象经过第二、三、四象限,则有(　A　)‎ ‎(A)01‎ ‎(C)a>1,b<-1 (D)a>1,b>1‎ 解析:因为a>1时,函数为增函数,必定过第一象限,所以当函数经过第二、三、四象限一定有00,a≠1)的反函数为g(x),且满足g(2)<0,则函数g(x+1)的图象是图中的(　A　)‎ 解析:令y=f(x)=ax,则x=logay,‎ 所以g(x)=logax.‎ 又g(2)<0,所以01,则实数a的取值范围是(　B　)‎ ‎(A)(-2,1) (B)(-∞,-2)∪(1,+∞)‎ ‎(C)(1,+∞) (D)(-∞,-1)∪(0,+∞)‎ 解析:当a≤0时,f(a)=()a-3>1,解得a<-2;‎ - 7 -‎ 当a>0时,f(a)=>1,解得a>1.‎ 综上,a的取值范围是(-∞,-2)∪(1,+∞),故选B.‎ ‎10.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=2x,则f(-2)等于(　B　)‎ ‎(A) (B)-4 (C)- (D)4‎ 解析:因为f(x)为奇函数,所以f(-2)=-f(2)=-22=-4.‎ ‎11.已知函数y=loga(x+c)(a,c为常数,其中a>0,a≠1)的图象如图,则下列结论成立的是(　D　)‎ ‎(A)a>1,c>1‎ ‎(B)a>1,01‎ ‎(D)00时是由函数y=logax的图象向左平移c个单位得到的,所以根据题中图象可知0b>c (B)b>c>a ‎(C)c>a>b (D)c>b>a 解析:因为1a>b.故选C.‎ 二、填空题(本大题共4小题,每小题5分,共20分)‎ - 7 -‎ ‎13.化简(log43+log83)(log32+log92)=　　　　. ‎ 解析:原式=(+)(+)‎ ‎=log23·=.‎ 答案:‎ ‎14.若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,其图象经过点(,a),则f(x)=　　 　　. ‎ 解析:y=f(x)=logax,过点(,a),代入后得loga=a,解得a=,所以函数是f(x)=lox.‎ 答案:lox ‎15.若函数f(x)=2|x-a|(a∈R)满足f(1+x)=f(1-x),且f(x)在[m,+∞)上单调递增,则实数m的最小值为　　 　　. ‎ 解析:因为f(1+x)=f(1-x),所以函数f(x)关于直线x=1对称,所以a=1,所以函数f(x)=2|x-1|的图象如图所示,因为函数f(x)在[m,+∞)上单调递增,所以m≥1,所以实数m的最小值为1.‎ 答案:1‎ ‎16.已知函数f(x)是定义在R上的偶函数,且在区间 [0,+∞)上单调递增.若实数a满足f(log‎2a)+f(loa)≤‎2f(1),则a的取值范围是　　　 　. ‎ 解析:因为f(loa)=f(-log‎2a)=f(log‎2a),‎ 所以原不等式可化为f(log‎2a)≤f(1).‎ 又因为f(x)在区间[0,+∞)上单调递增,‎ 所以0≤log‎2a≤1,即1≤a≤2.‎ 因为f(x)是偶函数,所以f(log‎2a)≤f(-1).‎ 又f(x)在区间(-∞,0]上单调递减,‎ 所以-1≤log‎2a≤0,所以≤a≤1.‎ 综上可知≤a≤2.‎ - 7 -‎ 答案:[,2]‎ 三、解答题(共40分)‎ ‎17.(本小题满分8分)‎ 计算:(1)(3)-(5)0.5+0.00÷0.0×;‎ ‎(2)2(lg )2+lg ·lg 5+.‎ 解:(1)原式=()-()+()÷×=-+25××=-+2=.‎ ‎(2)原式=(lg 2)2+lg 2(1-lg 2)+=(lg 2)2+lg 2-(lg 2)2+ 1-lg 2=1.‎ ‎18.(本小题满分10分)‎ 如果函数y=a2x+2ax-1(a>0且a≠1)在[-1,1]上的最大值为14,求a 的值.‎ 解:令ax=t,则y=t2+2t-1=(t+1)2-2,其对称轴t=-1,二次函数在[-1, +∞)上单调递增,‎ 又ax=t,且x∈[-1,1],所以t=ax∈[a-1,a](a>1)或t∈[a,a-1](01时,取t=a,即x=1时,ymax=a2+‎2a-1=14,解得a=3或a=-5(舍去);‎ 当00,+1>0,+1>0,‎ 所以f(x2)>f(x1),‎ 所以f(x)为R上的增函数.‎ ‎(3)解:f(x)==1-,‎ 因为3x>0⇒3x+1>1⇒0<<2⇒-2<-<0,‎ - 7 -‎ 所以-1<1-<1,‎ 即f(x)的值域为(-1,1).‎ - 7 -‎