江苏省启东中学2021届高三上学期期初考试数学试题（PDF含答案版） 10页

高二数学试卷 第 1 页 共 10 页 2020～2021 学年第一学期期初考试试题答案 高三数学 命题人： 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的四个选项中， 只有一项是符合题目要求的。 1．设全集  1,2,3,4U  ，集合    1,3 , 4S T  ，则 C S T  等于（ ） A． 2,4 B． 4 C． D． 1,3,4 【答案】A 2 ． 在 ABC 中 ， E 为 AC 上 一 点 ， 3   AC AE ， P 为 BE 上 任 一 点 ， 若 ( 0, 0)       AP mAB nAC m n ，则 3 1 m n 的最小值是（ ） A．9 B．10 C．11 D．12 【答案】D 3．已知 Ra  ，则“ 1a  ”是“ 1 1a  ”的（ ） A．充分非必要条件 B．必要非充分条件 C．充要条件 D．既非充分又非必要条件 【答案】A 4．设     ,0 1 2 1 , 1 x xf x x x       ,若    1f a f a  ,则 1f a      （ ） A．2 B．4 C．6 D．8 【答案】C 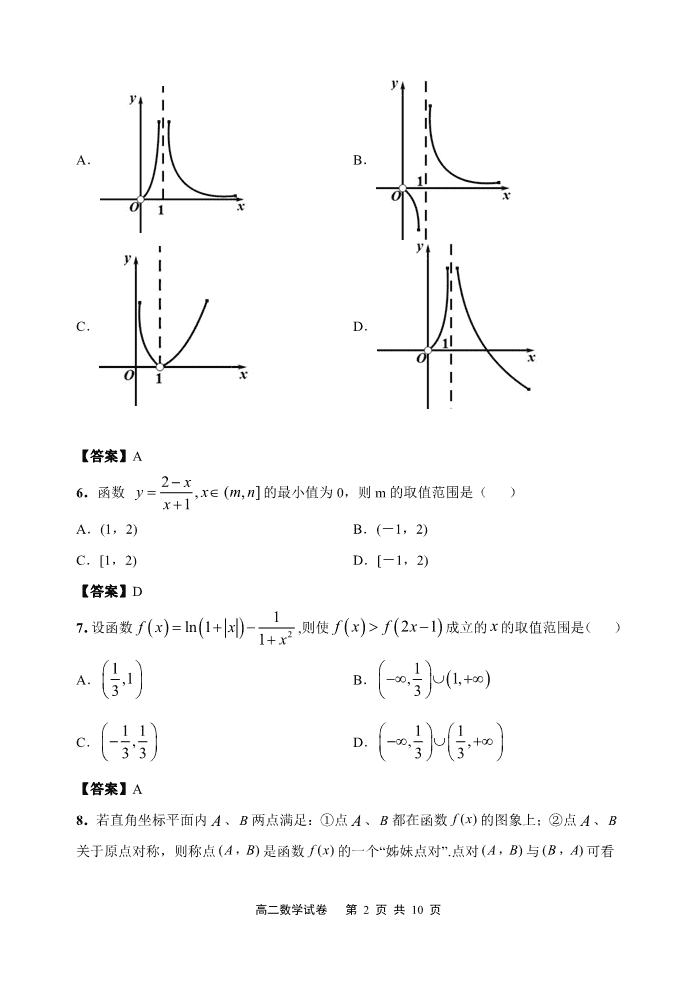5．已知函数 2( ) ln( 1)f x x x    ,则函数 ( 1) y f x 的图象大致为（ ） 高二数学试卷 第 2 页 共 10 页 A． B． C． D． 【答案】A 6．函数 2 , ( , ]1 xy x m nx   的最小值为 0，则 m 的取值范围是（ ） A．(1，2) B．(－1，2) C．[1，2) D．[－1，2) 【答案】D 7．设函数     2 1ln 1 1f x x x     ,则使    2 1f x f x  成立的 x 的取值范围是（ ） A． 1 ,13      B．  1, 1,3       C． 1 1,3 3     D． 1 1, ,3 3             【答案】A 8．若直角坐标平面内 A 、B 两点满足：①点 A 、B 都在函数 ( )f x 的图象上；②点 A 、B 关于原点对称，则称点 ( )A B， 是函数 ( )f x 的一个“姊妹点对”.点对 ( )A B， 与 ( )B A， 可看 高二数学试卷 第 3 页 共 10 页 作是同一个“姊妹点对”，已知函数 2 2 0 ( ) 2 0x x x x f x xe      ，则 ( )f x 的“姊妹点对”有（ ） A． 0 个 B．1个 C． 2 个 D．3 个 【答案】C 二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分。在每小题给出的选项中，有多 项符合题目要求。全部选对的得 5 分，部分选对的得 3 分，有选错的得 0 分。 9．下列命题正确的是（ ） A．若随机变量  ~ 100,X B p ，且   20E X  ，则 1 1 52D X       B．已知函数  f x 是定义在 R 上的偶函数，且在[0, ) 上单调递减  1 0f  ，则不等式  2log 0f x  的解集为 1 ,22      C．已知 xR ，则“ 0x  ”是“ 1 1x   ”的充分不必要条件 D．根据一组样本数据的散点图判断出两个变量线性相关，由最小二乘法求得其回归直线 方程为 ˆ 0.3y x m  ，若样本中心点为 , 2.8m  ，则 4m  【答案】BD 10．设 a ，b ， c 为实数且 a b ，则下列不等式一定成立的是（ ） A． 1 1 a b  B． 2020 1a b  C． ln lna b D．    2 21 1a c b c   【答案】BD 11．关于函数 1 2( ) 1 1xf x x e      下列结论正确的是（ ） A．图像关于 y 轴对称 B．图像关于原点对称 C．在 ,0 上单调递增 D．  f x 恒大于 0 高二数学试卷 第 4 页 共 10 页 【答案】ACD 12 ． 已 知 定 义 在 R 上 的 函 数 f(x) 的 图 象 连 续 不 断 ， 若 存 在 常 数 ( )t t R ， 使 得 ( ) ( ) 0f x t tf x   对任意的实数 x 成立，则称 f(x)是回旋函数． 给出下列四个命题中，正确的命题是（ ） A．常值函数 ( ) ( 0)f x a a  为回旋函数的充要条件是 t= -1; B．若 (0 1)xy a a   为回旋函数，则 t>l; C．函数 2( )f x x 不是回 旋函数； D．若 f(x)是 t=2 的回旋函数，则 f(x)在[0,4030]上至少有 2015 个零点． 【答案】ACD 三、填空题：本题共 4 小题，每小题 5 分，共 20 分。请把答案直接填写在答题卡相应．．．．． 位置上．．．。 13．已知 4log 9a ， 2log 5b ，则 22  a b __________. 【答案】45 14．已知 a R ，命题“存在 x R ，使 2 3 0  x ax a ”为假命题，则 a 的取值范围为 __________. 【答案】  12,0 15．已知数列 na 的首项为 4 ，且满足    12 1 0n nn a na n N      ，则下列命题： ① na n     是等差数列；② na 是递增数列；③设函数   2 1 1 2 x n n af x x a          ，则存在 某个区间   , 1n n n N   ，使得  f x 在 , 1n n  上有唯一零点；则其中正确的命题序 号为__________. 【答案】②③ 16．已知集合  0 0 1A x x   .给定一个函数 ( )y f x ，定义集合 高二数学试卷 第 5 页 共 10 页  1( ),n nA y y f x x A    ,若 1n nA A   对任意的 *n N 成立，则称该函数 ( )y f x 具有性质“ ” (I)具有性质“ ”的一个一次函数的解析式可以是_________； (Ⅱ)给出下列函数：① 1y x ；② 2 1 y x ；③ cos( ) 22  y x ，其中具有性质“ ” 的函数的序号是_________．(本题第一空 2 分，第二空 3 分) 【答案】 1 y x （答案不唯一） ①② 四、解答题：本题共 6 小题，共 70 分。请在答题卡指定区域．．．．．．．内作答。解答时应写出文字 说明、证明过程或演算步骤。 17．(本小题满分 10 分) 已知集合   2| log 3 3A x x   ，  | 2 1 3B x m x m     . （1）若 3m  ，则 A B ； （2）若 A B B ，求实数 m 的取值范围. 【解析】 （1）若 3m  ，则  | 5 6B x x   ， 依题意      2 2 2| log 3 3 | log 3 log 8A x x x x       | 3 5x x    ， 故  | 3 6A B x x    ； （2）因为 A B B ，故 B A ； 若 2 1 3m m   ，即 4m≥ 时， B   ，符合题意； 若 2 1 3m m   ，即 4m  时， 2 1 3 3 5 m m       ， 解得 1 2m   ； 综上所述，实数 m 的取值范围为   1,2 4,  . 高二数学试卷 第 6 页 共 10 页 18．(本小题满分 12 分) 已知    23 6 6f x x a a x     . (1)解关于 a 的不等式  1 0f  ； (2)若不等式  f x b 的解集为  1,3 ，求实数 ,a b 的值． 【解析】 (1)∵f(x)＝－3x2＋a(6－a)x＋6， ∴f(1)＝－3＋a(6－a)＋6＝－a2＋6a＋3， ∴原不等式可化为 a2－6a－3<0，解得 3－2 3 b 的解集为(－1,3)等价于方程－3x2＋a(6－a)x＋6－b＝0 的两根为－1,3， 等价于  61+3= 3 61 3= 3 a a b       解得 3 3 3 a b      . 19．(本小题满分 12 分) 设函数 2( ) (ln 1)f x x a x   . （1）当 1a  时，求 ( )y f x 在点 (1, (1))f 处的切线方程； （2）当 2 ea  时，判断函数 ( )f x 在区间 0, 2 a      是否存在零点？并证明. 【解析】 （Ⅰ）  f x 的定义域为  0,  ,   1f x ax    ,若 0a  ,则   0f x  ,  f x 在 0,  是 高二数学试卷 第 7 页 共 10 页 单调递增；若 0a  ,则当 10,x a     时   0f x  ,当 1 ,x a      时   0f x  ,所以  f x 在 10, a      单调递增,在 1 ,a     单调递减. （Ⅱ）由（Ⅰ）知当 0a  时  f x 在 0,  无最大值,当 0a  时  f x 在 1x a  取得最大 值,最大值为 1 1 1ln 1 ln 1.f a a aa a a                       因此 1 2 2 ln 1 0f a a aa           .令   ln 1g a a a   ,则  g a 在 0,  是增函 数,  1 0g  ,于是,当 0 1a  时,   0g a  ,当 1a  时   0g a  ,因此 a 的取值范围是  0,1 . 20．(本小题满分 12 分) 某乡镇响应“绿水青山就是金山银山”的号召，因地制宜的将该镇打造成“生态水果特色 小镇”．经调研发现：某珍稀水果树的单株产量W （单位：千克）与施用肥料 x （单位： 千克）满足如下关系：  25 3 , 0 2 ( ) 50 , 2 51 x x W x x xx         ，肥料成本投入为10x 元，其它成 本投入（如培育管理、施肥等人工费） 20x 元．已知这种水果的市场售价大约为 15 元／ 千克，且销路畅通供不应求．记该水果树的单株利润为 ( )f x （单位：元）． （Ⅰ）求 ( )f x 的函数关系式； （Ⅱ）当施用肥料为多少千克时，该水果树的单株利润最大?最大利润是多少? 【解析】 （Ⅰ）由已知      15 20 10 15 30f x W x x x W x x      215 5 3 30 ,0 2, 5015 30 , 2 51 x x x x x xx             275 30 225,0 2, 750 30 , 2 5.1 x x x x x xx           高二数学试卷 第 8 页 共 10 页 (Ⅱ)由(Ⅰ)得     2 2 175 222,0 2,75 30 225,0 2, 5=750 30 , 2 5. 25780 30 1 , 2 5.1 1 x xx x x f x x x x x xx x                                 当 0 2x  时，    max 2 465f x f  ； 当 2 5x  时，    25780 30 11f x xx         25780 30 2 1 4801 xx       当且仅当 25 11 xx   时，即 4x  时等号成立． 因为 465 480 ，所以当 4x  时，  max 480f x  ． ∴当施用肥料为 4 千克时，种植该果树获得的最大利润是 480 元． 21．(本小题满分 12 分) 已知 a∈R，函数 f（x）=x2﹣2ax+5. （1）若 a>1，且函数 f（x）的定义域和值域均为[1，a]，求实数 a 的值； （2）若不等式 x|f（x）﹣x2|  1 对 x∈[ 1 3 ， 1 2 ]恒成立，求实数 a 的取值范围. 【解析】 （1）∵f（x）的图象开口向上，对称轴为 x=a>1， ∴f（x）在[1，a]上单调递减， ∴f（1）=a，即 6﹣2a＝a，解得 a=2.. （2）不等式 x|f（x）﹣x2| 1 对 x∈[ 1 3 ， 1 2 ]恒成立， 即 x|2ax﹣5| 1 对 x∈[ 1 3 ， 1 2 ]恒成立， 故 a 2 5 1 2 x x  且 a 2 5 1 2 x x  在 x∈[ 1 3 ， 1 2 ]恒成立， 令 g（x） 2 2 5 1 1 1 5 25 2 2 2 8          x x x ，x∈[ 1 3 ， 1 2 ]， 高二数学试卷 第 9 页 共 10 页 所以 g（x）max=g（ 2 5 ） 25 8  ， 所以 25 8a  . 令 h（x） 2 2 5 1 1 1 5 25 2 2 2 8         x x x ，x∈[ 1 3 ， 1 2 ]， 所以 h（x）min=h（ 1 2 ）=7， 所以 7a  . 综上： 25 78 a  . 22．(本小题满分 12 分) 已知定义域为 R 的   2 2   x x bf x a 函数是奇函数． （1）求 ,a b 的值； （2）用定义证明  f x 在 ,  上为减函数； （3）若对于任意 t R ，不等式    2 22 2 0   f t t f t k 恒成立，求 k 的范围． 【解析】 （1）∵ ( )f x 为 R 上的奇函数，∴ (0) 0f  ， 1b  . 又 ，得 1a  . 经检验 1 1a b ， 符合题意. （2）任取 1 2x x R， ，且 1 2x x ，则 1 2 1 2 2 1 1 2 1 21 2 1 2 1 2 (1 2 )(2 1) (1 2 )(2 1)( ) ( ) 2 1 2 1 (2 1)(2 1) x x x x x x x x x xf x f x              高二数学试卷 第 10 页 共 10 页 2 1 1 2 2(2 2 ) (2 1)(2 +1) x x x x   . ∵ 1 2x x ，∴ 1 22 2 0x x  ，又∴ 1 2(2 1)(2 1) 0x x   ， ∴ 1 2( ) ( ) 0f x f x  ，∴ ( )f x 为 R 上的减函数 （3）∵ t R ，不等式 2 2( 2 ) (2 ) 0f t t f t k    恒成立， ∴ 2 2( 2 ) (2 )f t t f t k    ， ∴ ( )f x 为奇函数，∴ 2 2( 2 ) ( 2 )f t t f k t   ， ∴ ( )f x 为减函数，∴ 2 22 2t t k t   . 即 23 2k t t  恒成立，而 2 21 1 13 2 3( )3 3 3t t t      ， ∴ 1 3k  