江苏省海门市东洲国际学校2020届高三数学综合训练（线上教学）（含附加题，无答案） 6页

高三数学综合训练（线上教学） 20200328‎ 一、填空题（本大题共 14 小题，共 70 分）‎ ‎1. 已知集合 A={x|x2-x-2≤0}，集合 B={x|1＜x≤3}，则 A∪B= ．‎ ‎2. 已知 a，b∈R，i 是虚数单位，若 a+i=1-bi，则（a+bi）8= ．‎ ‎3. 从某班抽取 5 名学生测量身高（单位：cm），得到的数据为 160，162，159，160，159，则该组 数据的方差 s2= ．[来源:学科网]‎ ‎4. 若双曲线 x2+my2=1 过点（-，2），则该双曲线的虚轴长为 ．‎ ‎5. 根据如图所示的伪代码，可知输出的结果 S 为 ．‎ ‎6. 在三张奖券中有一、二等奖各一张，另一张无奖，甲乙两人各抽取一张（不 放回），两人都中奖的概率为 ．‎ ‎7. 已知正四棱锥的底面边长是，侧棱长是 ，则该正四棱锥的体积为 ．‎ ‎8. 设函数 y=f（x）（x∈R）则“y=|f（x）|是偶函数”是“y=f（x）的图象关于原点对称”的 ‎ 条件．（填“充分不必要”，“必要不充分”，“充要”，“既不充分也不必要”）‎ ‎9. 如图，在平面四边形 ABCD 中，若 AC=3，BD=2，则= ‎ ‎10. 在△ABC 中，已知 AB=2，AC2-BC2=6，则 tanC 的最大值是 ．‎ ‎11. 在平面直角坐标系 xOy 中，已知圆 C1：(x-4)2+(y-8)2＝1，圆 C2：(x-6)2+(y+6)2＝9．若 圆心在 x 轴上的圆 C 同时平分圆 C1 和圆 C2 的圆周，则圆 C 的方程是 ．[来源:学科网]‎ ‎12. 已知{an}，{bn}均为等比数列，其前 n 项和分别为 Sn，Tn，若对任意的 n∈N*，总有 = ，‎ 则 = ．‎ ‎13. 已知 x，y，z 均为正数，，x+2y+2z=xyz，则 xyz 的最大值为 ．‎ ‎14. 已知函数，且 y=f（x）在 x∈[0，2]上的最大值为，若函数 g（x）‎ ‎=f（x）-ax2 有四个不同的零点，则实数 a 的取值范围为 ． 二、解答题 ‎15. 如图，在四棱锥 E-ABCD 中，已知底面 ABCD 为平行四边形，AE⊥BC，三角形 BCE 为锐角三角形， 面 AEB⊥面 BCE，设 F 为 CE 的中点．‎ 求证：（1）AE∥面 BDF；（2）AE⊥面 BCE．‎ ‎[来源:Zxxk.Com]‎ ‎16. 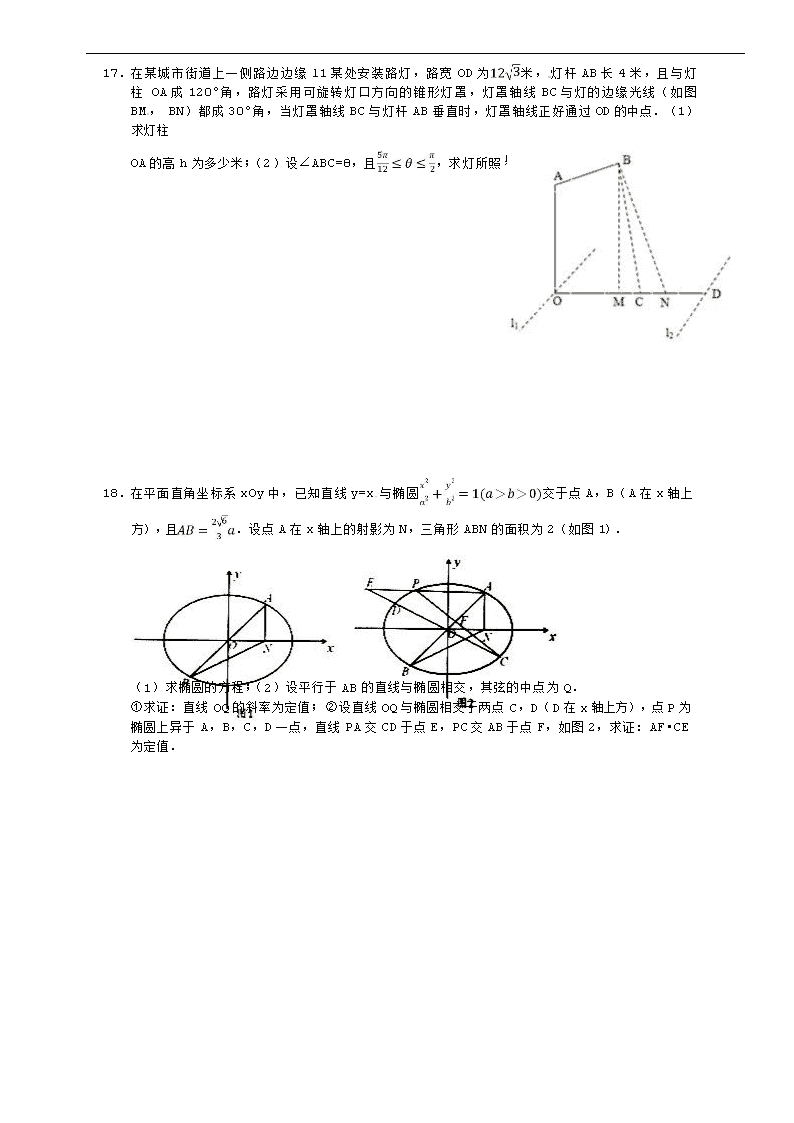在△ABC 中，．‎ ‎（1）求角 C 的大小；（2）若 CD⊥AB，垂足为 D，且 CD=4，求△ABC 面积的最小值．‎ ‎17. 在某城市街道上一侧路边边缘 l1 某处安装路灯，路宽 OD 为米，灯杆 AB 长 ‎4 米，且与灯柱 OA 成 120°角，路灯采用可旋转灯口方向的锥形灯罩，灯罩轴线 BC 与灯的边缘光线（如图 BM， BN）都成 30°角，当灯罩轴线 BC 与灯杆 AB 垂直时，灯罩轴线正好通过 OD 的中点．（1）求灯柱 射路面宽度 MN 的最小值．‎ OA 的高 h 为多少米；（2）设∠ABC=θ，且，求灯所照 ‎18. 在平面直角坐标系 xOy 中，已知直线 y=x 与椭圆交于点 A，B（A 在 x 轴上 方），且 ．设点 A 在 x 轴上的射影为 N，三角形 ABN 的面积为 2（如图 1）．‎ ‎[来源:学科网ZXXK]‎ ‎（1）求椭圆的方程；（2）设平行于 AB 的直线与椭圆相交，其弦的中点为 Q．‎ ‎①求证：直线 OQ 的斜率为定值；②设直线 OQ 与椭圆相交于两点 C，D（D 在 x 轴上方），点 P 为 椭圆上异于 A，B，C，D 一点，直线 PA 交 CD 于点 E，PC 交 AB 于点 F，如图 2，求证：AF•CE 为定值．‎ ‎19. 已知函数 f（x）=exx3-2x2+（a+4）x‎-2a-4]，其中 a∈R，e 为自然对数的底数．‎ ‎（1）关于 x 的不等式 f（x）＜-ex 在（-∞，2）上恒成立，求 a 的取值范围；‎ ‎（2）讨论函数 f（x）极值点的个数．‎ ‎20. 若无穷数列{an}满足：只要 ap=aq（p，q∈N*），必有 ap+1=aq+1，则称{an}具有性质 P．‎ ‎（Ⅰ）若{an}具有性质 P，且 a1=1，a2=3，a4=1，a6+a7+a8=19，求 a3；‎ ‎（Ⅱ）若无穷数列{bn}是等差数列，无穷数列{cn}是等比数列，b1=c4=1，b4=c1=64，an=bn+cn． 判断{an}是否具有性质 P，并说明理由；‎ ‎（Ⅲ）设{bn}是无穷数列，已知 an+1=bn+sinan（n∈N*）．求证：“对任意 a1，{an}都具有 性质 P”的充要条件为“{bn}是常数列”．‎ 高三数学综合训练（线上教学） 附加题 ‎ ‎21. 已知矩阵 M 对应的变换将点（-5，-7）变换为（2，1），其逆矩阵 M-1 有特征值-1，对应的一个 特征向量为 ，求矩阵 M．[来源:Z*xx*k.Com]‎ ‎22. 在平面直角坐标系 xoy 中，以 O 为极点，x 轴的正半轴为极轴，取相同的单位长度，建立极坐标 系，已知曲线 C1 的参数方程为，（ ，α为参数），曲线 C2 的极坐标方程为 ‎，求曲线 C1 与曲线 C2 的交点的直角坐标．‎ ‎23. 如图，已知正四棱锥 P-ABCD 中，PA=AB=2，点 M，N 分别在 PA，BD 上，且= = ．‎ ‎（1）求异面直线 MN 与 PC 所成角的大小；‎ ‎（2）求二面角 N-PC-B 的余弦值．‎ ‎24. 已知数列{an}的通项公式为 an=（n≥1，n∈N*）．‎ ‎（Ⅰ）求 a1，a2，a3 的值；‎ ‎（Ⅱ）求证：对任意的自然数 n∈N*，不等式 a1•a2…an＜2•n!成立．‎