高二数学人教a必修5练习：3-3-1二元一次不等式（组）与平面区域word版含解析 6页

§3.3 二元一次不等式(组)与简单的线性规划问题 3．3.1 二元一次不等式(组)与平面区域 课时目标 1．了解二元一次不等式表示的平面区域． 2．会画出二元一次不等式(组)表示的平面区域． 1．二元一次不等式(组)的概念 含有两个未知数，并且未知数的次数是 1 的不等式叫做二元一次不等式． 由几个二元一次不等式组成的不等式组称为二元一次不等式组． 2．二元一次不等式表示的平面区域 在平面直角坐标系中，二元一次不等式 Ax＋By＋C>0 表示直线 Ax＋By＋C＝0 某一侧 所有点组成的平面区域，把直线画成虚线以表示区域不包括边界． 不等式 Ax＋By＋C≥0 表示的平面区域包括边界，把边界画成实线． 3．二元一次不等式(组)表示平面区域的确定 (1)直线 Ax＋By＋C＝0 同一侧的所有点的坐标(x，y)代入 Ax＋By＋C 所得的符号都相同． (2)在直线 Ax＋By＋C＝0 的一侧取某个特殊点(x0，y0)，由 Ax0＋By0＋C 的符号可以断 定 Ax＋By＋C>0 表示的是直线 Ax＋By＋C＝0 哪一侧的平面区域． 一、选择题 1．如图所示，表示阴影部分的二元一次不等式组是( ) A. y≥－2 3x－2y＋6>0 x<0 B. y≥－2 3x－2y＋6≥0 x≤0 C. y>－2 3x－2y＋6>0 x≤0 D. 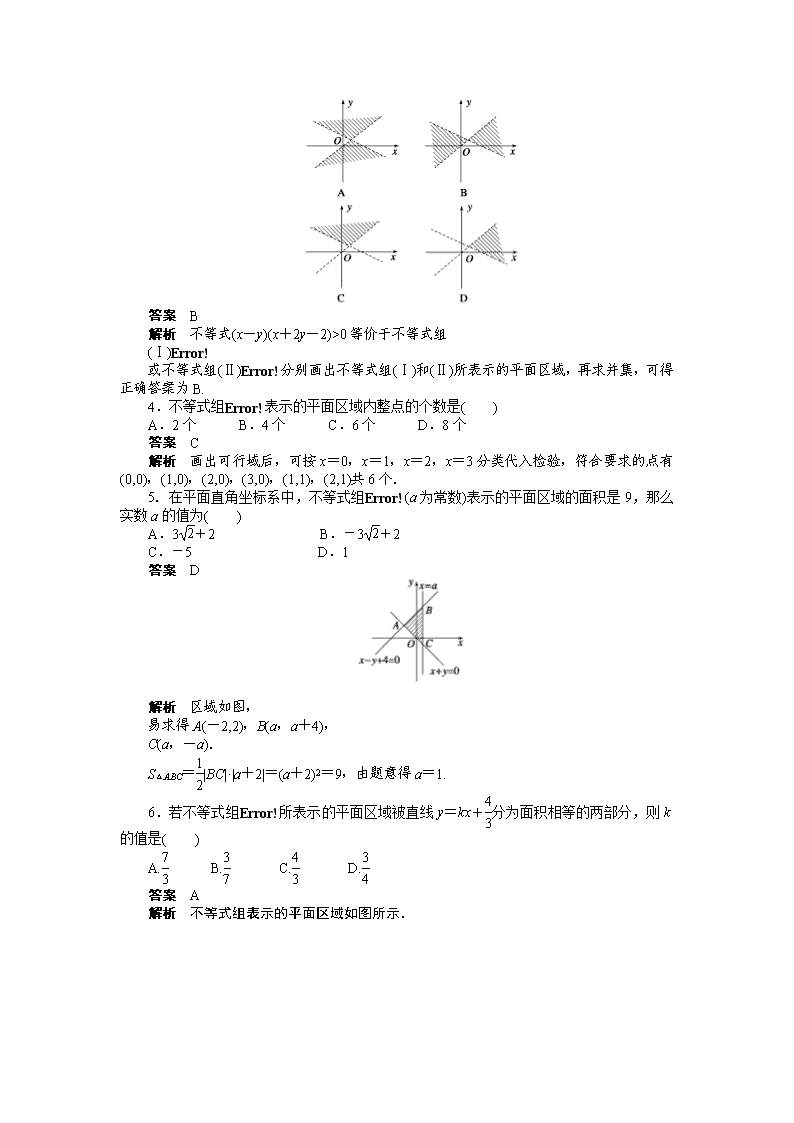y>－2 3x－2y＋6<0 x<0 答案 C 解析 可结合图形，根据确定二元一次不等式组表示的平面区域的方法逆着进行．由图 知所给区域的三个边界中，有两个是虚的，所以 C 正确． 2．已知点(－1,2)和(3，－3)在直线 3x＋y－a＝0 的两侧，则 a 的取值范围是( ) A．(－1,6) B．(－6,1) C．(－∞，－1)∪(6，＋∞) D．(－∞，－6)∪(1，＋∞) 答案 A 解析 由题意知，(－3＋2－a)(9－3－a)<0， 即(a＋1)(a－6)<0，∴－10 的点(x，y)所在的区域为( ) 答案 B 解析 不等式(x－y)(x＋2y－2)>0 等价于不等式组 (Ⅰ) x－y>0， x＋2y－2>0 或不等式组(Ⅱ) x－y<0， x＋2y－2<0. 分别画出不等式组(Ⅰ)和(Ⅱ)所表示的平面区域，再求并 集，可得正确答案为 B. 4．不等式组 4x＋3y≤12， x－y>－1， y≥0 表示的平面区域内整点的个数是( ) A．2 个 B．4 个 C．6 个 D．8 个 答案 C 解析 画出可行域后，可按 x＝0，x＝1，x＝2，x＝3 分类代入检验，符合要求的点有(0,0)， (1,0)，(2,0)，(3,0)，(1,1)，(2,1)共 6 个． 5．在平面直角坐标系中，不等式组 x＋y≥0， x－y＋4≥0， x≤a (a 为常数)表示的平面区域的面 积是 9，那么实数 a 的值为( ) A．3 2＋2 B．－3 2＋2 C．－5 D．1 答案 D 解析 区域如图， 易求得 A(－2,2)，B(a，a＋4)， C(a，－a)． S△ABC＝1 2|BC|·|a＋2|＝(a＋2)2＝9，由题意得 a＝1. 6．若不等式组 x≥0， x＋3y≥4， 3x＋y≤4 所表示的平面区域被直线 y＝kx＋4 3 分为面积相等的两部 分，则 k 的值是( ) A.7 3 B.3 7 C.4 3 D.3 4 答案 A 解析 不等式组表示的平面区域如图所示． 由于直线 y＝kx＋4 3 过定点 0，4 3 .因此只有直线过 AB 中点时，直线 y＝kx＋4 3 能平分平面 区域． 因为 A(1,1)，B(0,4)，所以 AB 中点 M 1 2 ，5 2 . 当 y＝kx＋4 3 过点 1 2 ，5 2 时，5 2 ＝k 2 ＋4 3 ， 所以 k＝7 3. 二、填空题 7．△ABC 的三个顶点坐标为 A(3，－1)，B(－1,1)，C(1,3)，则△ABC 的内部及边界所 对应的二元一次不等式组是________________． 答案 x＋2y－1≥0 x－y＋2≥0 2x＋y－5≤0 解析 如图直线 AB 的方程为 x＋2y－1＝0(可用两点式或点斜式写出)． 直线 AC 的方程为 2x＋y－5＝0， 直线 BC 的方程为 x－y＋2＝0， 把(0,0)代入 2x＋y－5＝－5<0， ∴AC 左下方的区域为 2x＋y－5<0. ∴同理可得△ABC 区域(含边界)为 x＋2y－1≥0 x－y＋2≥0 2x＋y－5≤0 . 8．已知 x，y 为非负整数，则满足 x＋y≤2 的点(x，y)共有________个． 答案 6 解析 由题意点(x，y)的坐标应满足 x∈N y∈N x＋y≤2 ，由图可知，整数点有(0,0)，(1,0)， (2,0)(0,1)(0,2)(1,1)6 个． 9．原点与点(1,1)有且仅有一个点在不等式 2x－y＋a>0 表示的平面区域内，则 a 的取值 范围为________． 答案 －10 a＋1≤0 .无解． ②原点(0,0)不在该区域内，点(1,1)在该区域内， 则 a≤0 a＋1>0 ，∴－11，y＝ax 恰好经过 A 点时，由 a2＝9，得 a＝3. 要满足题意， 需满足 a2≤9，解得 14 3 时，表示区域是△AOB； 当 x＋y＝a 过 B(1,0)时表示的区域是△DOB，此时 a＝1； 当 0