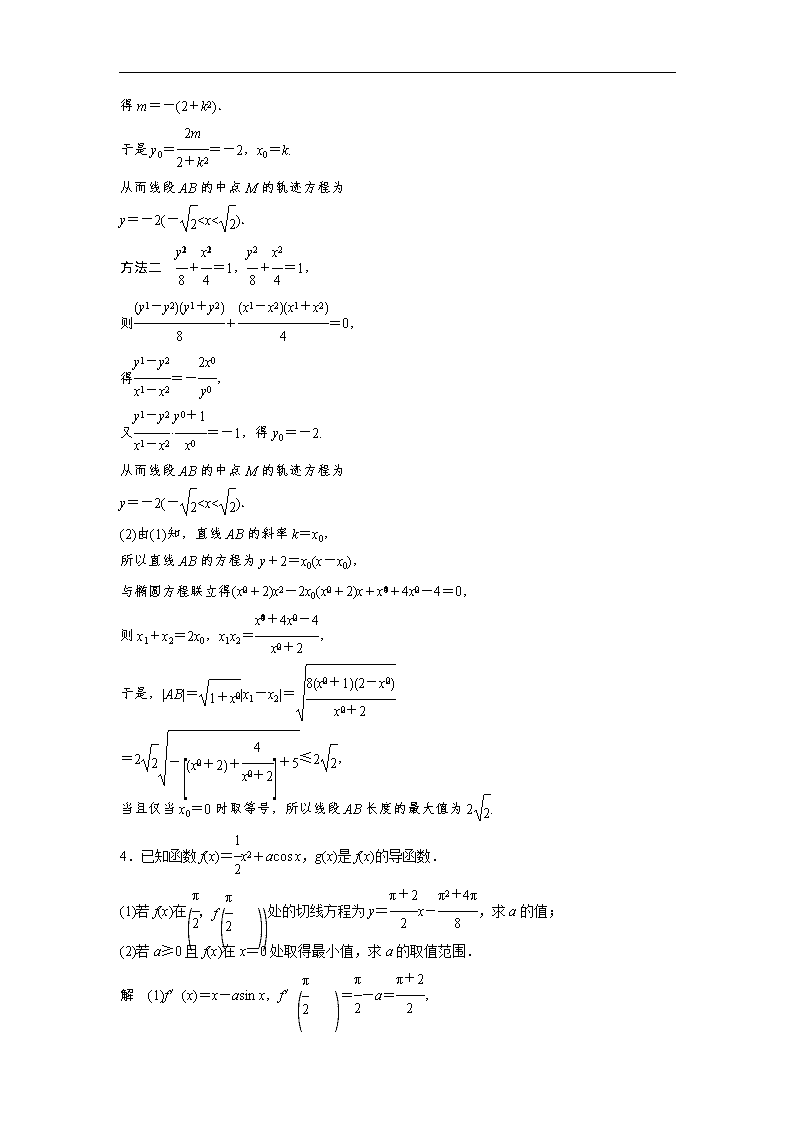2019年高考数学练习题汇总解答题滚动练3 4页

解答题滚动练3‎ ‎1．已知函数f(x)＝Asin(ωx＋φ)的图象经过三点，，，且在区间内有唯一的最值，且为最小值．‎ ‎(1)求出函数f(x)＝Asin的解析式；‎ ‎(2)在△ABC中，a，b，c分别是角A，B，C的对边，若f ＝且bc＝1，b＋c＝3，求a的值．‎ 解　(1)由题意可得函数的周期T＝2＝π，‎ ‎∴ω＝2，又由题意可知，当x＝时，y＝0，‎ ‎∴Asin＝0，∴2×＋φ＝kπ(k∈Z)，‎ ‎∵0<φ<，∴φ＝.‎ 再由题意得当x＝0时，y＝，‎ ‎∴Asin ＝，∴A＝，‎ ‎∴f(x)＝sin.‎ ‎(2)∵f ＝，‎ ‎∴sin＝，‎ ‎∴A＋＝＋2kπ(k∈Z)．‎ 又A∈(0，π)，∴A＝.‎ ‎∵bc＝1，b＋c＝3，‎ ‎∴由余弦定理，得a2＝b2＋c2－2bccos A＝b2＋c2－bc＝(b＋c)2－3bc＝9－3＝6，‎ ‎∴a＝.‎ ‎2．已知数列{an}满足Sn＝2an－n(n∈N*)．‎ ‎(1)证明：{an＋1}是等比数列；‎ ‎(2)求a1＋a3＋a5＋…＋a2n＋1(n∈N*)．‎ ‎(1)证明　由S1＝2a1－1，得a1＝1，‎ 因为Sn－Sn－1＝2an－n－[2an－1－(n－1)](n≥2)，‎ 所以an＝2an－1＋1(n≥2)，‎ 从而由an＋1＝2(an－1＋1)，‎ 得＝2(n≥2)，‎ 所以{an＋1}是以2为首项，2为公比的等比数列．‎ ‎(2)解　由(1)得an＝2n－1，‎ 所以a1＋a3＋a5＋…＋a2n＋1 ‎ ‎＝－ ‎ ‎＝－ ‎＝(n∈N*)．‎ ‎3.已知两个不同的动点A，B在椭圆＋＝1上，且线段AB的垂直平分线恒过点P(0，－1).‎ ‎(1)求线段AB中点M的轨迹方程；‎ ‎(2)求线段AB长度的最大值．‎ 解　(1)设A(x1，y1)，B(x2，y2)，M(x0，y0)，易知直线AB的斜率存在，‎ 方法一　设直线AB的方程为y＝kx＋m，‎ 联立 得(2＋k2)x2＋2kmx＋m2－8＝0，(*)‎ 则x0＝＝－，‎ y0＝kx0＋m＝，‎ 所以kMP＝＝＝－，‎ 得m＝－(2＋k2)．‎ 于是y0＝＝－2，x0＝k.‎ 从而线段AB的中点M的轨迹方程为 y＝－2(－