吉林省长春市2021届高三第一次质量监测（一模）数学理试题 Word版含解析 9页

长春市2021届高三第一次质量监测（一模）‎ 理科数学 一、选择题:本题共12小题，每小题5分，共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.‎ ‎1.已知集合则集合的元素个数有 A. 1个 B. 2个 C. 3个 D. 4个 ‎2.函数是 A.周期为的奇函数 B.周期为的偶函数 C.周期为的奇函数 D.周期为的偶函数 ‎3.在中, 是的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎4.张老师居住的一条街上,行驶着甲、乙两路公交车,这两路公交车的数目相同,并且都是每隔十分钟就到达车站一辆(即停即走).张老师每天早晨都是在6:00到6:10之间到达车站乘车到学校,这两条公交线路对他是一样的,都可以到达学校,甲路公交车的到站时间是6:09,‎ ‎6:19，6:29,6:39，…,乙路公交车的到站时间是6:00,6:10,6:20,6:30,…，则张老师乘坐上甲路公交车的概率是 A. 10% B. 50% C. 60% D. 90%‎ ‎5.长江流域内某地南北两岸平行,如图所示已知游船在静水中的 河流两岸示意图 航行速度的大小,水流的速度的大小 ‎,设和所成角为，若游船 要从航行到正北方向上位于北岸的码头处,则等于 A. B. C. D. ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎6.已知函数则函数在上的大致图象为 ‎ A B C D ‎7.将长、宽分别为和的长方形沿对角线折起,得到四面体,‎ 则四面体的外接球体积为 - 9 -‎ A. B. C. D. ‎ ‎ 1 / 2‎ ‎8.已知抛物线，过其焦点的直线与抛物线分别交于、两点(点在第一象限)，且则直线的倾斜角为 A. B. C. D. 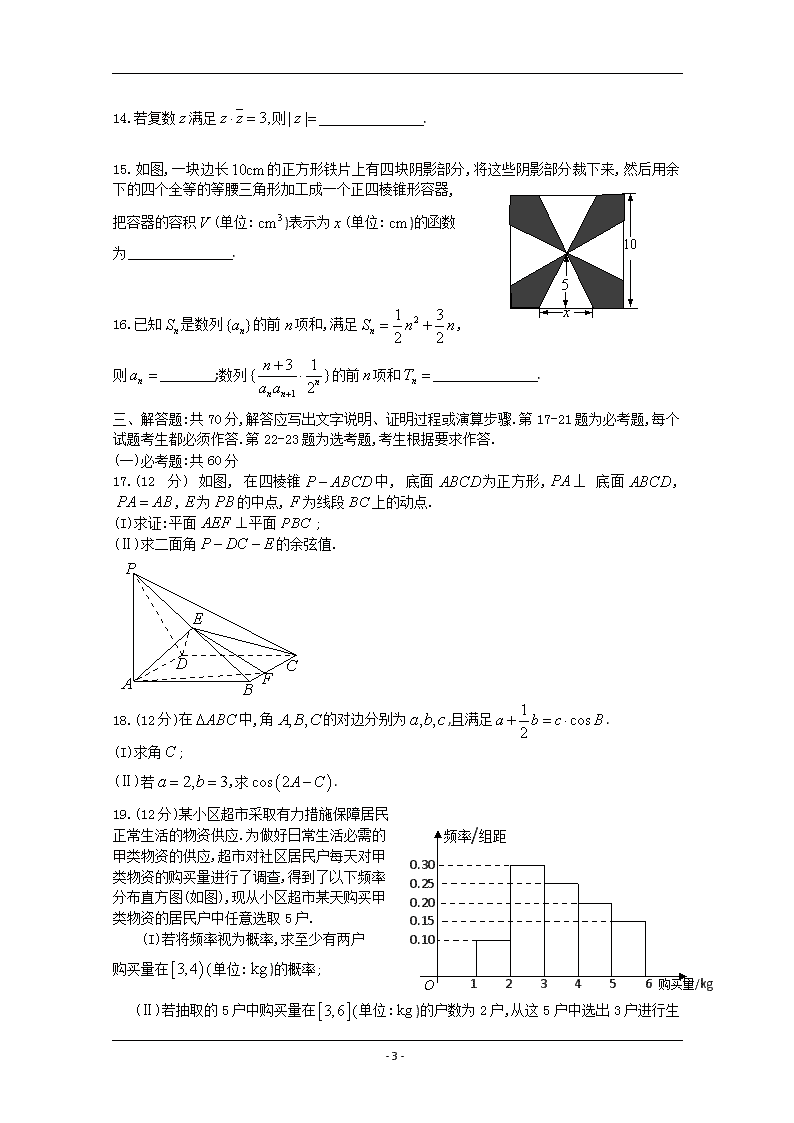‎ ‎9.对于函数下列结论中正确的是 为奇函数 在定义域上是单调递减函数 的图象关于点对称 在区间上存在零点 ‎10.如图,在面积为1的正方形内做四边形使 以此类推,在四边形内再 做四边形……，记四边形的面积为 ‎，则 ‎ ‎ ‎ ‎ ‎11.双曲线被斜率为的直线截得的弦的中点为则双曲线的离心率为 ‎ ‎ ‎12.已知偶函数满足当时则的值为 ‎ ‎ 二、填空题:本题共4小题,每小题5分,共20分.‎ ‎13.若则 .‎ - 9 -‎ ‎14.若复数满足则 .‎ ‎15.如图,一块边长的正方形铁片上有四块阴影部分,将这些阴影部分裁下来,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,‎ 把容器的容积(单位:)表示为(单位:)的函数 为 .‎ ‎16.已知是数列的前项和,满足,‎ 则 ;数列的前项和 .‎ 三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22-23题为选考题,考生根据要求作答.‎ ‎(一)必考题:共60分 ‎17.(12分)如图,在四棱锥中,底面为正方形,⊥底面,,为的中点,为线段上的动点.‎ ‎(I)求证:平面平面;‎ ‎(Ⅱ)求二面角的余弦值.‎ ‎18.(12分)在中,角的对边分别为,且满足.‎ ‎(I)求角;‎ ‎(Ⅱ)若,求.‎ ‎ 1 2 3 4 5 6 购买量/kg ‎ ‎0.30‎ ‎0.25‎ ‎0.20‎ ‎0.15‎ ‎0.10‎ 频率/组距 ‎19.(12分)某小区超市采取有力措施保障居民 正常生活的物资供应.为做好日常生活必需的 甲类物资的供应,超市对社区居民户每天对甲 类物资的购买量进行了调查,得到了以下频率 分布直方图(如图),现从小区超市某天购买甲 类物资的居民户中任意选取5户.‎ ‎(I)若将频率视为概率,求至少有两户 购买量在单位:)的概率;‎ ‎(Ⅱ)若抽取的5户中购买量在单位:)‎ - 9 -‎ 的户数为2户,从这5户中选出3户进行生活情况调查,记3户中需求量在单位:)的户数为ξ,求ξ的分布列和期望.‎ ‎20.(12分)‎ 已知椭圆,直线分别与轴轴交于两点,与椭圆交于两点.‎ ‎(I)若求直线的方程;‎ ‎(Ⅱ)若点的坐标为求面积的最大值.‎ ‎21.(12分)‎ 设函数.‎ ‎(I)当时,求函数的单调区间;‎ ‎(Ⅱ)当时,求证:‎ ‎(二)选考题:共10分,请考生在22、23题中任选一题作答,如果多做则按所做的第一题计分.‎ ‎22.【选修4-4坐标系与参数方程](10分)‎ 已知直线的参数方程为(为参数),以坐标原点为极点,轴的非负半轴为极轴建立极坐标系,圆的极坐标方程为 ‎(I)求直线的普通方程和圆的直角坐标方程;‎ ‎(Ⅱ)若直线与圆相交于两点,求 ‎23.[选修4-5不等式选讲](10分)‎ 已知 ‎(I)求证:;‎ ‎(Ⅱ)求证:.‎ - 9 -‎ 长春市2021届高三质量监测数学(理科)试题参考答案及评分参考 一,选择题(本大题共12小题，每小题5分，共60分)‎ ‎1. B.【解题思路】所以故选B.‎ ‎2.D【解想思路】故且为偶函数,故选D ‎3．C【解题思路】易知在三角形中，是的充要条件,故选C ‎4.D【解思路】张老师到达车站在6：00-6:10中是等可能的,故张老师在6:00-6:09到达车站 的概率为90%,故有90%的可能乘坐甲路公交车，故选D ‎5．B【解题思路】由题意知有所以选B.‎ ‎6．A【解题思路】由可得的图象关于直线对称,排除BC,‎ 当时排除D,数选A.‎ ‎7. A【解题思路】中点到A,B,C,D的距离均为1,故球的体积为,故选A.‎ ‎8．C【解题思路】如图,过A,B作AA’,BB’垂直准线,垂足为A’,B’，过B作AA’垂 线,垂足为C,由抛物线定义知所以,,所以直线倾斜角为,故选C.‎ ‎9.C【解题思路】由图象可知,图象关于点对称,因此不是奇函数,在定义域内函数为增函数,在上有零点,故选C.‎ ‎10.B【解题思路】由图可知所以其前项和为,故选B.‎ ‎11.B【解题思路】设代入双曲线方程作差有,有,所以 - 9 -‎ 故选B.‎ ‎12. A【解题思路】由题意可知函数的周期为4,又当 时则当时则 故选A 二、填空题(本大题共4小题,每小题5分，共20分)‎ ‎13. 【解题思路】‎ ‎14. 【解题思路】设有 ‎15. 【解题思路】由题意可知,正四棱锥的高为,所以容积 ‎16. ，【解题思路】,所以 ‎,故的前项和.‎ 三，简答题 ‎17.【答案】(1)因为,E为PB中点,所以 因为平面ABCD,所以 由所以BC⊥平面PAB,所以又 所以AE⊥平面PAB,所以平面平面PAB.‎ ‎(2)法1:取中点G,连结GE,GD,由,‎ 所以故平面EDC,因为PA⊥平面ABCD,所以由 所以CD⊥平面PAD,所以所以∠PDG为二面角 的平面角,在中所以(12分)‎ - 9 -‎ 法2:以A为原点,AB,AD,AP为x,y,z轴,建立空间直角坐标系,有 设平面PCD的一个法向量为平面 ECD的一个法向量为有，，‎ 又，,所以 即二面角 P-DC-E的余弦值为(12分)‎ ‎18. 【答案】(1)由正弦定理知 有,所以（6分）‎ 所以，‎ ‎，,所以(12分)‎ ‎19．【答案】分)‎ ‎(2) 的可能值为0,1,2‎ ‎；；‎ ξ的分布列为 ‎20．【答案】(1)设联立直线方程与椭圆方程有 有有，‎ - 9 -‎ 所以AB中点坐标为 由中点坐标为 因为所以线段MN的中点与AB的中点重合,有 解得(6分)‎ ‎(2)由(1)可知 因为所以 所以当k=0时面积最大.(12分)‎ ‎21.【答案】时，令可化为即 易知为增函数,且 所以当时单调递减,当时单调递增 又,‎ 所以当时单调递增,当时单调递减.(4分)‎ ‎(2)令可化为 ‎,当时,易知为上增函数,‎ 当时；当时；当时,‎ 而 - 9 -‎ 所以存在即 当t∈时单调递减,‎ 当t∈时单调递增:‎ 所以.(12分)‎ ‎22.【答案】(1)直线的普通方程是,圆的直角坐标方程是 ‎（5分）‎ ‎(2)圆心(1,2)到直线的距离圆半径所以|（10分）‎ ‎23.【答案】(1)证明:因为, ‎ 所以,(当且仅当时取等号)(5分)‎ ‎(2)因为,所以 所以 ‎,当且仅当时取等号(10分)‎ - 9 -‎