2020年北京市高考数学试卷【word版本试题；可编辑；含答案】 10页

1 / 10 2020 年北京市高考数学试卷 一、选择题 1.已知集合퐴 = {−1,0,1,2}，퐵 = {푥|0 < 푥 < 3}，则퐴 ∩ 퐵 =() A.{−1,0,1} B.{0,1} C.{−1,1,2} D.{1,2} 2.在复平面内，复数푧对应的点的坐标是(1,2)，则푖 ⋅ 푧 =() A.1 + 2푖 B.−2 + 푖 C.1 − 2푖 D.−2 − 푖 3.在(√푥 − 2)5的展开式中，푥2的系数为() A.−5 B.5 C.−10 D.10 4.某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为 () A.6 + √3 B.6 + 2√3 C.12 + √3 D.12 + 2√3 5.已知半径为1的圆经过点(3,4)，则其圆心到原点的距离的最小值为() A.4 B.5 C.6 D.7 6.已知函数푓(푥) = 2푥 − 푥 − 1，则不等式푓(푥) > 0的解集是() A.(−1,1) B.(−∞, −1) ∪ (1, +∞) C.(0,1) D.(−∞, 0) ∪ (1, +∞) 7.设抛物线的顶点为푂，焦点为퐹，准线为푙，푃是抛物线异于푂的一点，过 푃做푃푄 ⊥ 푙于푄，则线段퐹푄的垂直平分线() A.经过点푂 B.经过点푃 C.平行于直线푂푃 D.垂直于直线푂푃 8.在等差数列{푎푛}中，푎1 = −9，푎5 = −1，记푇푛 = 푎1푎2 ⋯ 푎푛(푛 = 1,2, … )， 则数列{푇푛}() A.有最大项，有最小项 B.有最大项，无最小项 C.无最大项，有最小项 D.无最大项，无最小项 9.已知훼，훽 ∈ R，则“存在푘 ∈ Z，使得훼 = 푘휋 + (−1)푘훽"是“sin훼 = sin훽”的() A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 10.2020年3月14日是全球首个国际圆周率日(휋퐷푎푦).历史上，求圆周率휋 的方法有多种，与中国传统数学中的“割圆术”相似，数学家阿尔·卡西 的方法是：当正整数푛充分大时，计算单位圆的内接正6푛边形的周长和外 切正6푛边形（各边均与圆相切的正6푛边形）的周长，将它们的算术平均 数作为2휋的近似值.按照阿尔·卡西的方法，휋的近似值的表达方式是() A.3푛(sin 30∘ 푛 + tan 30∘ 푛 ) B.6푛(sin 30∘ 푛 + tan 30∘ 푛 ) C.3푛(sin 60∘ 푛 + tan 60∘ 푛 ) D.6푛(sin 60∘ 푛 + tan 60∘ 푛 ) 二、填空题 11.函数푓(푥) = 1 푥+1 + ln푥的定义域是________. 12.已知双曲线퐶: 푥2 6 − 푦2 3 = 1，则퐶的右焦点的坐标为________；퐶的焦点 2 / 10 到其渐近线的距离是________. 13.已知正方形퐴퐵퐶퐷的边长为2，点푃满足퐴푃 → = 1 2 (퐴퐵 → + 퐴퐶 → )，则 |푃퐷 → | =________；푃퐵 → ⋅ 푃퐷 → =________. 14.若函数푓(푥) = sin(푥 + 휑) + cos푥的最大值为2，则常数휑的一个取值 为________. 15.为满足人民对美好生活的向往，环保部门要求相关企业加强污水治理， 排放未达标的企业要限期整改．设企业的污水排放量푊与时间푡的关系为 푊 = 푓(푡)，用− 푓(푏)−푓(푎) 푏−푎 的大小评价在[푎, 푏]这段时间内企业污水治理能力 的强弱．已知整改期内，甲、乙两企业的污水排放量与时间的关系如下图 所示． 给出下列四个结论： ①在[푡1, 푡2]这段时间内，甲企业的污水治理能力比乙企业强； ②在푡2时刻，甲企业的污水治理能力比乙企业强； ③在푡3时刻，甲、乙两企业的污水排放量都已达标； ④甲企业在[0, 푡1]，[푡1, 푡2]，[푡2, 푡3]这三段时间中，在[0, 푡1]的污水治理能 力最强． 其中所有正确结论的序号是________. 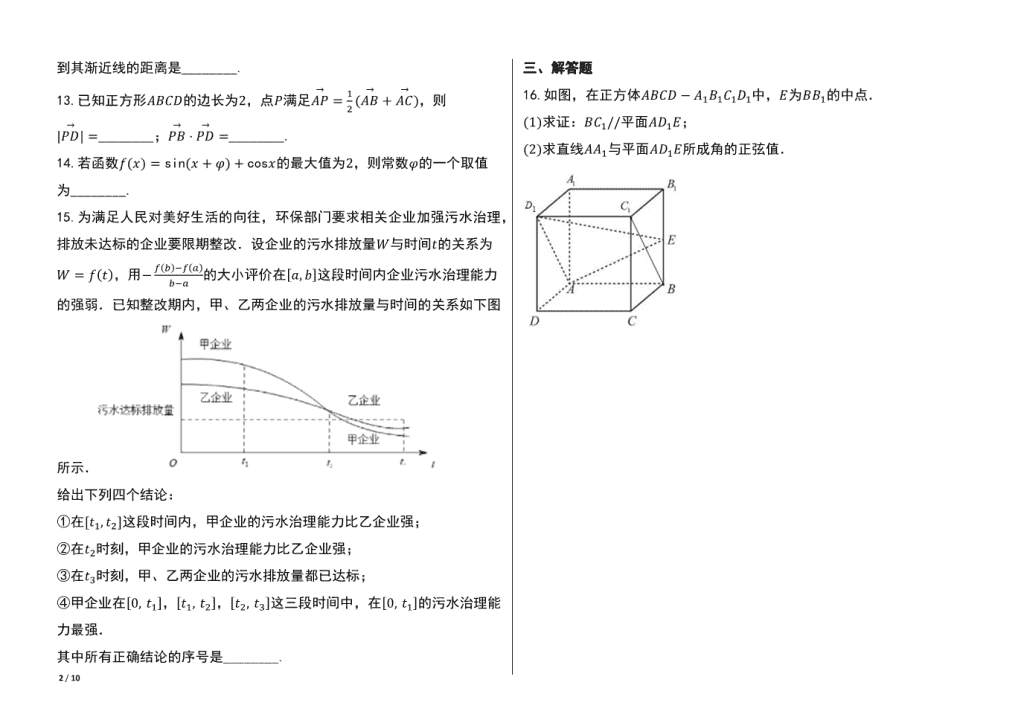三、解答题 16.如图，在正方体퐴퐵퐶퐷 − 퐴1퐵1퐶1퐷1中，퐸为퐵퐵1的中点． (1)求证：퐵퐶1//平面퐴퐷1퐸； (2)求直线퐴퐴1与平面퐴퐷1퐸所成角的正弦值． 3 / 10 17.在△ 퐴퐵퐶中，푎 + 푏 = 11，再从条件①、条件②这两个条件中选择一 个作为已知，求： (1)푎的值； (2)sin퐶和△ 퐴퐵퐶的面积. 条件①：푐 = 7，cos퐴 = − 1 7 ； 条件②：cos퐴 = 1 8 ，cos퐵 = 9 16 . 18.某校为举办甲乙两项不同活动，分别设计了相应的活动方案：方案一、 方案二，为了解该校学生对活动方案是否支持，对学生进行简单随机抽样， 获得数据如下表： 男生 女生 支持 不支持 支持 不支持 方案一 200人 400人 300人 100人 方案二 350人 250人 150人 250人 假设所有学生对活动方案是否支持相互独立． (1)分别估计该校男生支持方案一的概率，该校女生支持方案一的概率； (2)从该校全体男生中随机抽取2人，全体女生中随机抽取1人，估计这3人 中恰有2人支持方案一的概率； (3)将该校学生支持方案二的概率估计值记为푃0，假设该校一年级有500名 男生和300名女生，除一年级外其他年级学生支持方案二的概率估计值记 为푃1，试比较푃0与푃1的大小．（结论不要求证明） 4 / 10 19.已知函数푓(푥) = 12 − 푥2. (1)求曲线푦 = 푓(푥)的斜率等于−2的切线方程； (2)设曲线푦 = 푓(푥)在点(푡, 푓(푡))处的切线与坐标轴围成的三角形面积为 푆(푡)，求푆(푡)的最小值． 20.已知椭圆퐶： 푥2 푎2 + 푦2 푏2 = 1过点퐴(−2, −1)，且푎 = 2푏. (1)求椭圆퐶的方程． (2)过点퐵(−4,  0)的直线푙交椭圆퐶于点푀，푁，直线푀퐴，푁퐴分别交直线 푥 = −4于点푃，푄，求|푃퐵| |퐵푄| 的值. 5 / 10 21.已知{푎푛}是无穷数列，给出两个性质： ①对于{푎푛}中任意两项푎푖，푎푗(푖 > 푗)，在{푎푛}中都存在一项푎푚，使得푎푖 2 푎푗 = 푎푚. ②对于{푎푛}中任意一项푎푛(푛 ≥ 3)，在{푎푛}都存在两项푎푘, 푎푙(푘 > 푙)，使得 푎푛 = 푎푘 2 푎푙 . (1)若푎푛 = 푛(푛 = 1,2, ⋯ )，判断{푎푛}是否满足性质①，说明理由； (2)若푎푛 = 2푛−1(푛 = 1,2, ⋯ )，判断数列{푎푛}是否同时满足性质①和性质②， 说明理由； (3)若{푎푛}是递增数列，且同时满足性质①和性质②，证明：{푎푛}为等比 数列． 6 / 10 参考答案与试题解析 2020 年北京市高考数学试卷 一、选择题 1.D 2.B 3.C 4.D 5.A 6.D 7.B 8.B 9.C 10.A 二、填空题 11.(0, +∞) 12.(3,  0),√3 13.√5,−1 14.휋 2 (答案不唯一) 15.①②③ 三、解答题 16.(1)证明：在正方体퐴퐵퐶퐷 − 퐴1퐵1퐶1퐷1中， 퐴퐵//퐷1퐶1且퐴퐵 = 퐷1퐶1， ∴四边形퐴퐵퐶1퐷1为平行四边形， ∴퐵퐶1//퐴퐷1， 又퐵퐶1 ⊄平面퐴퐷1퐸， 퐴퐷1 ⊂平面퐴퐷1퐸， ∴퐵퐶1//平面퐴퐷1퐸. (2)解：建立如图所示的空间直角坐标系： 设正方体的棱长为2， 则퐴(0,0,0)，퐴1(0,0,2)，퐷1(2,0,2)， ∵퐸为퐵퐵1的中点， ∴퐸(0,2,1)， ∴퐴퐴1 → = (0,0,2)，퐴퐷1 → = (2,0,2)，퐴퐸 → = (0,2,1)， 设平面퐴퐷1퐸的法向量为푛→ = (푥, 푦, 푧)， 则{푛→ ⋅ 퐴퐷1 → = 0， 푛→ ⋅ 퐴퐸 → = 0， ∴{2푥 + 2푧 = 0， 2푦 + 푧 = 0， 令푥 = 1，则可得푧 = −1，푦 = 1 2 ， ∴푛→ = (1, 1 2 , −1）， 设直线퐴퐴1与平面퐴퐷1퐸所成角为훼， ∴sin훼 = |cos < 퐴퐴1 → , 푛→ > | = |퐴퐴1 → ⋅푛→| |퐴퐴1 → |⋅|푛→| 7 / 10 = 2 2×√1+1 4+1 = 2 3 ， 则直线퐴퐴1与平面퐴퐷1퐸所成角的正弦值为2 3 . 17.解：(1)选①由余弦定理푎2 = 푏2 + 푐2 − 2푏푐cos퐴， 得푎2 = (11 − 푎)2 + 49 − 2(11 − 푎) × 7 × (− 1 7)， ∴푎 = 8. 选②∵cos퐴 = 1 8 ，퐴 ∈ (0, 휋 2)， ∴sin퐴 = 3√7 8 . ∵cos퐵 = 9 16 ，퐵 ∈ (0, 휋 2)， ∴sin퐵 = 5√7 16 . 由正弦定理 푎 sin퐴 = 푏 sin퐵 ， 则 푎 3√7 8 = 11−푎 5√7 16 ， ∴푎 = 6. (2)选①∵cos퐴 = − 1 7 ，퐴 ∈ (0, 휋)， ∴sin퐴 = 4√3 7 . 由正弦定理 푎 sin퐴 = 푐 sin퐶 ， 则sin퐶 = 푐sin퐴 푎 = 7×4√3 7 8 = √3 2 ， ∴푆△퐴퐵퐶 = 1 2 푎푏sin퐶 = 1 2 × 8 × (11 − 8) × √3 2 = 6√3. 选②sin퐶 = sin(퐴 + 퐵) = sin퐴cos퐵 + cos퐴sin퐵 = √7 4 . ∵푎 + 푏 = 11， ∴푏 = 5， ∴푆△퐴퐵퐶 = 1 2 푎푏sin퐶 = 1 2 × 6 × 5 × √7 4 = 15 4 √7. 18.解：(1)该校男生支持方案一的概率푃1 = 200 200+400 = 1 3 ， 该校女生支持方案一的概率푃2 = 300 300+100 = 3 4 . (2)푃 = (1 − 1 3) × 1 3 × 3 4 + 1 3 × (1 − 1 3) × 3 4 + 1 3 × 1 3 × (1 − 3 4) = 13 36 . (3)푃0 > 푃1. 男生女生整体比率600: 400，男生对方案二支持率高于女生； 而一年级男生女生比为500：300，高于整体比值，方案二的支持占比高 于平均值， 所以其他年级支持率푃1小于푃0，푃0也小于一年级支持方案二的概率. 19.解：(1)因为푓(푥) = 12 − 푥2， 所以푓′(푥) = −2푥， 令−2푥 = −2，得푥 = 1，则푓(1) = 11， 所以曲线푦 = 푓(푥)的斜率等于−2的切线方程为： 푦 − 11 = −2(푥 − 1)， 即푦 = −2푥 + 13. (2)푓(푡) = 12 − 푡2，푓′(푡) = −2푡， 所以曲线푦 = 푓(푥)在点(푡, 푓(푡))处的切线方程为： 푦 − (12 − 푡2) = −2푡(푥 − 푡)， 若푡 = 0，则围不成三角形； 8 / 10 令푥 = 0，得푦 = 12 + 푡2， 令푦 = 0，得푥 = 12+푡2 2푡 ， 所以푆(푡) = 1 2 |12 + 푡2| ⋅ | 12+푡2 2푡 | = 1 4 (12+푡2)2 |푡| ， 因为其为偶函数，仅考虑푡 > 0即可， 푆(푡) = 1 4 (푡3 + 24푡 + 144 푡 )，푡 > 0， 푆′(푡) = 1 4 (3푡2 + 24 − 144 푡2 ) = 3 4푡2 (푡2 − 4)(푡2 + 12) = 3 4푡2 (푡 + 2)(푡 − 2)(푡2 + 12)， 当0 < 푡 < 2时，푆′(푡) < 0，푆(푡)在(0,2)上单调递减， 当푡 > 2时，푆′(푡) > 0，푆(푡)在(2, +∞)上单调递增， 所以푆(푡)在푡 = 2时，取得极小值， 极小值为最小值푆(푡)min = 푆(2) = 32. 20.解：(1)把点퐴(−2, −1)代入椭圆方程得： { 4 푎2 + 1 푏2 = 1， 푎 = 2푏， 解得{푎 = 2√2， 푏 = √2. 即椭圆퐶的方程为푥2 8 + 푦2 2 = 1. (2)当푙不与푥轴重合时，设푙的方程为푥 = 푡푦 − 4， 푀(푥1, 푦1)，푁(푥2, 푦2)，푃(−4,  푝)，푄(−4,  푞)， 联立푙与퐶可得：{푥 = 푡푦 − 4， 푥2 + 4푦2 = 8， 消去푥整理得：(푡2 + 4)푦2 − 8푡푦 + 8 = 0. ∴푦1 + 푦2 = 8푡 푡2+4 ，푦1푦2 = 8 푡+4 . 由퐾퐴푀 = 퐾퐴푃得到푝+1 −2 = 푦1+1 푥1+2 ， 即푝 = − 푥1+2푦1+4 푥1+2 ， 由퐾퐴푁 = 퐾퐴푄得到푞+1 −2 = 푦2+1 푥2+2 ， 即푞 = − 푥2+2푦2+4 푥2+2 ， ∴|푃퐵| |퐵푄| = |푝| |푞| = |(푥1 + 2푦1 + 4)(푥2 + 2) (푥2 + 2푦2 + 4)(푥1 + 2)| = |(푡2 + 2푡)푦1푦2 − 2(푡 + 2)푦1 (푡2 + 2푡)푦1푦2 − 2(푡 + 2)푦2 | = | (푡2 + 2푡) 8 푡2 + 4 − 2(푡 + 2)( 8푡 푡2 + 4 − 푦2) (푡2 + 2푡)푦1푦2 − 2(푡 + 2)푦2 | 9 / 10 = |−(푡2 + 2푡)푦1푦2 + 2(푡 + 2)푦1 (푡2 + 2푡)푦1푦2 − 2(푡 + 2)푦2 | = 1. 当푙与푥轴重合时，푥1 = −2√2，푥2 = 2√2， 푝 = − 푥1+4 푥1+2 ，푞 = − 푥2+4 푥2+2 ， ∴|푃퐵| |퐵푄| = |푝| |푞| = |(푥1 + 4)(푥2 + 2) (푥2 + 4)(푥1 + 2)| = 1. 综上所述，|푃퐵| |퐵푄| = 1. 21.(1)解：若푎푛 = 푛(푛 = 1,2, ⋯ )， {푎푛}不满足性质①，理由如下： 取푎3 = 3，푎2 = 2， 则푎32 푎2 = 9 2 ∉ N∗. (2)解：若푎푛 = 2푛−1(푛 = 1,2, ⋯ )，数列{푎푛}同时满足性质①和性质②. 对于{푎푛}中任意两项푎푖, 푎푗(푖 > 푗)， 푎푖 2 푎푗 = (2푖−1)2 2푗−1 = 22푖−푗−1 = 푎2푖−푗 = 푎푚， 即存在푚 = 2푖 − 푗，满足性质①. 对于{푎푛}中任意一项푎푛(푛 ≥ 3)， 푎푛 = 2푛−1 = 22푘−푙−1 = (푎푘)2 푎푙 ， 即存在푘, 푙使得푛 = 2푘 − 푙成立，满足性质②. (3)证明：(푖)若푎1 > 0则푎푛 > 0， 由性质②知，存在两项푎푘, 푎푙(푘 > 푙)， 使得푎3 = 푎푘 2 푎푙 = 푎푘 × 푎푘 푎푙 > 푎푘 > 푎푙， 所以푘 = 2，푙 = 1，即푎3 = 푎22 푎1 , 所以푎1, 푎2, 푎3成等比数列，设其公比为푞(푞 > 1). 由性质①知，푎32 푎2 = (푎1푞2)2 푎1푞 = 푎1푞3， (푎1푞3)2 푎1푞2 = 푎1푞4，(푎1푞4)2 푎1푞3 = 푎1푞5，⋯均为数列{푎푛}中的项. 由性质②知，在{푎푛}中存在两项푎푘1 ,푎푙1(푘1 > 푙1)，使得 푎4 = 푎푘1 2 푎푙1 = 푎1푞2푘1−푙1−1 > 푎3 = 푎1푞2， 即2푘1 − 푙1 − 1 > 2. 又푎32 푎2 = 푎1푞3为数列{푎푛}中的项， 所以푎4 = 푎1푞2푘1−푙1−1 ≤ 푎32 푎2 = 푎1푞3. 即2푘1 − 푙1 − 1 = 3，푎4 = 푎1푞3. 同理，可证푎5 = 푎1푞4，푎6 = 푎1푞5，……，푎푛 = 푎1푞푛−1，…… 即数列{푎푛}为首项为푎1 > 0，公比푞 > 1的等比数列. (푖푖)若푎1 < 0，假设푎2 > 0，则由性质①知， 在{푎푛}中都存在一项푎푚，使得푎22 푎1 = 푎푚 < 0， 此时푎2 > 0 > 푎푚 (푚 ≥ 3)，与{푎푛}是递增数列矛盾，即假设错误， 所以푎2 < 0. 10 / 10 同理，可证푎푛 < 0. 由性质②知，存在两项푎푘2, 푎푙2(푘2 > 푙2)， 使得푎3 = 푎푘2 2 푎푙2 = 푎푘2 × 푎푘2 푎푙2 > 푎푘2 > 푎푙2， 所以푘2 = 2，푙2 = 1，即푎3 = 푎22 푎1 , 所以푎1, 푎2, 푎3成等比数列，设其公比为푞(0 < 푞 < 1), 由(푖)，同理可证，数列{푎푛}为首项为푎1 < 0，公比푞 ∈ (0,1)的等比数列. 综上，原命题得证.