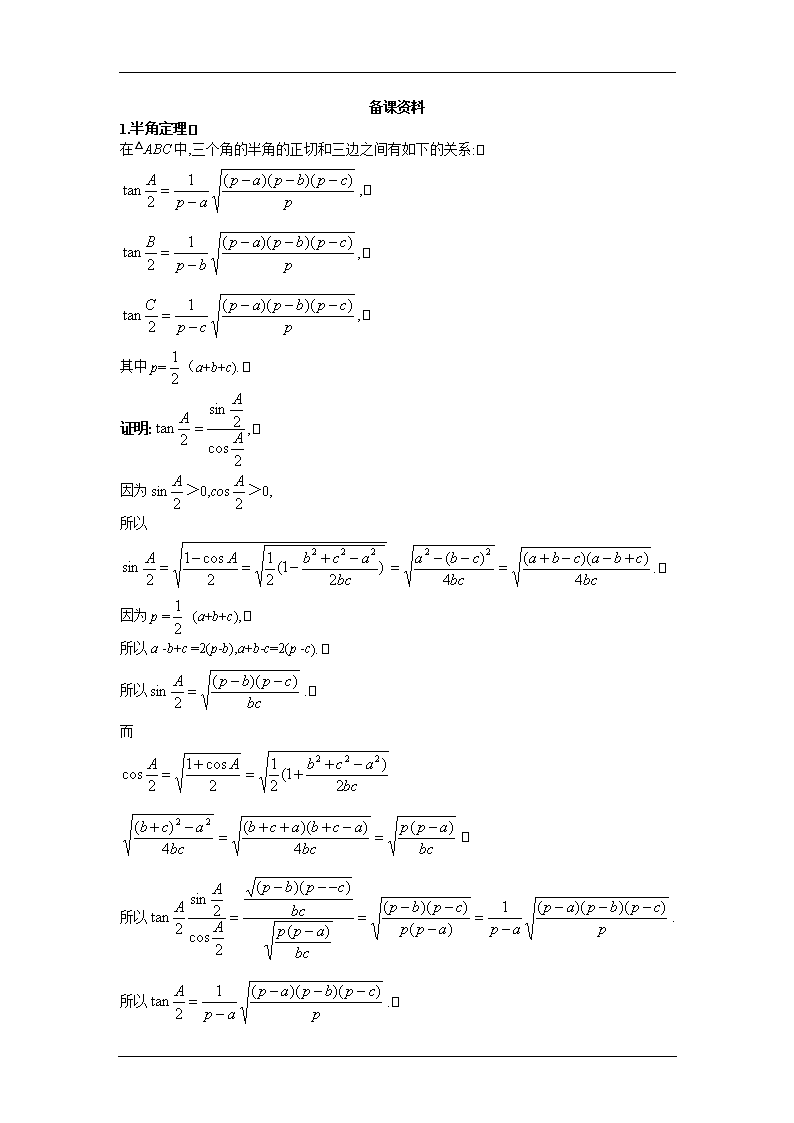人教新课标A版高一数学1-2-3解决有关测量角度的问题） 3页

备课资料 1.半角定理 在△ABC 中,三个角的半角的正切和三边之间有如下的关系: p cpbpap ap A ))()((1 2tan   , p cpbpap bp B ))()((1 2tan   , p cpbpap cp C ))()((1 2tan   , 其中 p= 2 1 （a+b+c). 证明: 2cos 2sin 2tan A A A  , 因为 sin 2 A ＞0,cos 2 A ＞0, 所以 bc cbacba bc cba bc acbAA 4 ))(( 4 )()21(2 1 2 cos1 2sin 22222  . 因为 p = 2 1 (a+b+c), 所以 a -b+c =2(p-b),a+b-c=2(p -c). 所以 bc cpbpA ))(( 2sin  . 而 bc acbAA 2 )1(2 1 2 cos1 2cos 222  bc app bc acbacb bc acb )( 4 ))(( 4 )( 22  所 以 p cpbpap apapp cpbp bc app bc cpbp A A A ))()((1 )( ))(( )( ))(( 2cos 2sin 2tan       . 所以 p cpbpap ap A ))()((1 2tan   . 同理,可得 p cpbpap bp B ))()((1 2tan   , p cpbpap cp C ))()((1 2tan  .从上面的证明过程中,我们可以得到用三角形的三 条边表示半角的正弦和半角的余弦的公式: bc appA bc cpbpA )( 2cos,))(( 2sin  . 同理可得 .)( 2cos)( 2cos,))(( 2sin,))(( 2sin ab cppC ac bppB ab bpapC ac cpapB  2.用三角形的三边表示它的内角平分线 设在△ABC 中(如右图),已知三边 a、b、c,如果三个角 A、B 和 C 的平分线分别是 tA、tB 和 tC， 那么，用已知边表示三条内角平分线的公式是： )(2 apbcpcbta  ; )(2 bpacpcatb  ; )(2 cpabpbatc  . 证明：设 AD 是角 A 的平分线，并且 BD=x，DC=y,那么，在△ADC 中，由余弦定理，得 tA 2=b2+y2-2bycosC,① 根据三角形内角平分线的性质，得 y x b c  , 所以 y yx b bc  . 因为 x+y=a, 所以 y a b bc  . 所以 cb aby  .② 将②代入①,得 Ccb abbcb abbta cos)(2)( 222  = ]cos)(22[)( 222 2 2 Ccbaabccbcb b  . 因为 bc cbaC 2cos 222  , 所以 ]2)(22[)( 222 222 2 2 2 ab cbacbabccbacb bta  = ))(()()2()( 2 222 2 acbcbacb bcabccbcb bc  = ),()( 4)(22)( 22 apbcpcbappcb bc  所以 )(2 apbcpcbta  . 同理,可得 )(2,)(2 cpabpbatbpacpcat cb  . 这就是已知三边求三角形内角平分线的公式. 3.用三角形的三边来表示它的外接圆的半径 设在△ABC 中,已知三边 a、b、c,那么用已知边表示外接圆半径 R 的公式是 ))()(( cpbpapp abcR   . 证明: 因为 AbcSA aR sin2 1,sin2  , 所以 bc SA 2sin  . 所以 ))()((4sin2 cpbpapp abc S abc A aR   .