人教版高中数学选修2-3练习：第三章章末复习课word版含解析 9页

章末复习课 整合·网络构建] 警示·易错提醒] 1．线性回归方程中的系数及相关指数 R2，独立性检验统计量 K2 公式复杂，莫记混用错． 2．相关系数 r 是判断两随机变量相关强度的统计量，相关指数 R2 是判断线性回归模型拟合效果好坏的统计量，而 K2 是判断两分类变 量相关程度的量，应注意区分． 3．在独立性检验中，当 K2≥6.635 时，我们有 99.9%的把握认为 两分类变量有关，是指“两分类变量有关”这一结论的可信度为 99% 而不是两分类变量有关系的概率为 99%. 专题一 回归分析思想的应用 回归分析是对抽取的样本进行分析，确定两个变量的相关关系， 并用一个变量的变化去推测另一个变量的变化．如果两个变量非线性 相关，我们可以通过对变量进行变换，转化为线性相关问题． 例 1] 一个车间为了规定工时定额，需确定加工零件所花费的时 间，为此进行了 10 次试验，测得的数据如下表所示： 零件数 x/个 10 20 30 40 50 60 70 80 90 100 加工时间 y/min 62 72 75 81 85 95 103 108 112 127 (1)画出散点图，并初步判断是否线性相关； (2)若线性相关，求线性回归方程； (3)求出相关指数； (4)作出残差图； (5)进行残差分析； (6)试制订加工 200 个零件的用时规定． 解：(1)散点图，如图所示： 由图可知，x，y 线性相关． (2)x 与 y 的关系可以用线性回归模型来拟合，不妨设回归模型为y ^ ＝a ^＋b ^ x.因为— x ＝55，— y ＝92， 0．670， a ^＝— y －b ^— x ＝92－553 825 ×55＝827 15 ≈55.133. 故线性回归方程为y ^＝0.670x＋55.133. 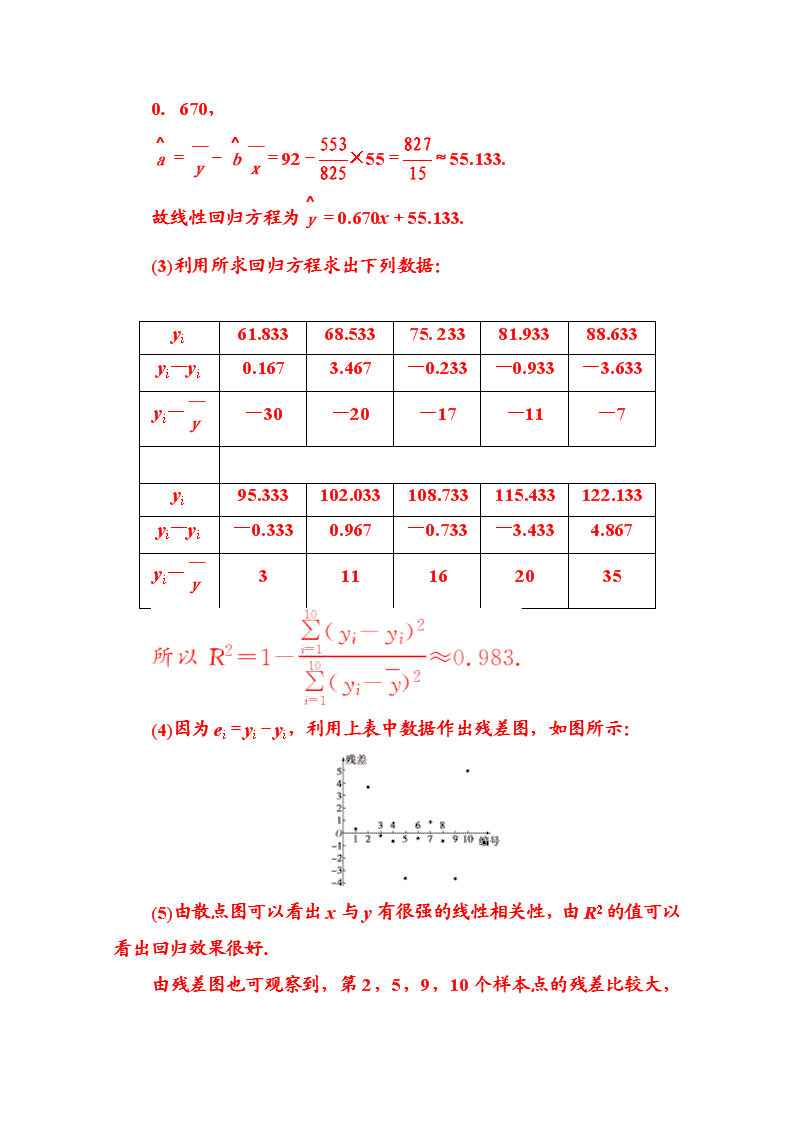(3)利用所求回归方程求出下列数据： yi 61.833 68.533 75. 233 81.933 88.633 yi－yi 0.167 3.467 －0.233 －0.933 －3.633 yi－— y －30 －20 －17 －11 －7 yi 95.333 102.033 108.733 115.433 122.133 yi－yi －0.333 0.967 －0.733 －3.433 4.867 yi－— y 3 11 16 20 35 (4)因为 ei＝yi－yi，利用上表中数据作出残差图，如图所示： (5)由散点图可以看出 x 与 y 有很强的线性相关性，由 R2 的值可以 看出回归效果很好． 由残差图也可观察到，第 2，5，9，10 个样本点的残差比较大， 需要确认在采集这些样本点的过程中是否有人为的错误． (6)将 x＝200 代入回归方程，得y ^＝189，所以可以制订 189 min 加 工 200 个零件的规定． 归纳升华 建立回归模型的一般步骤： (1)确定研究对象，明确哪个变量是解释变量，哪个变量是预报变 量； (2)画出确定好的解释变量和预报变量的散点图，观察它们之间的 关系(如是否存在线性关系)； (3)由经验确定回归方程的类型，如我们观察到数据呈线性关系， 选用线性回归方程y ^＝a ^＋b ^ x； (4)按一定规则估计回归方程中的参数； (5)得出结果后分析残差图是否有异常(个别数据对应的残差过大， 或残差呈现不随机的规律性，等等)，若残差存在异常，则应检查数据 是否有误，或模型是否合适等； (6)依据回归方程做出预报． 变式训练] 某商场经营一批进价是 30 元/台的小商品，在市场试 验中发现，此商品的销售单价 x(x 取整数)元与日销售量 y 台之间有如 下对应数据： 单价 x/元 35 40 45 50 日销售 y/台 56 41 28 11 (1)画出散点图并说明 y 与 x 是否具有线性相关关系？如果有，求 出线性回归方程(方程的斜率保留一个有效数字)； (2)设经营此商品的日销售利润为 P 元，根据(1)写出 P 关于 x 的函 数关系式，并预测当销售单价 x 为多少元时，才能获得最大日销售利 润． 解：散点图如图所示：从图中可以看出这些点大致分布在一条直 线附近，因此两个变量具有线性相关关系． 设回归直线方程为y ^＝a ^＋b ^ x，由题意知— x ＝42.5，— y ＝34, a ^＝— y －b ^— x ＝34－(－3)×42.5＝161.5. 所以y ^＝－3x＋161.5. (2)依题意有： P ＝ ( － 3x ＋ 161.5)(x － 30) ＝ － 3x2 ＋ 251.5x － 4 845 ＝ － 3 x－251.5 6 2＋251.52 12 －4 845. 所以当 x＝251.5 6 ≈42 时，P 有最大值． 即预测销售单价约为 42 元时，能获得最大日销售利润． 专题二 独立性检验的应用 独立性检验是对两个分类变量间是否存在相关关系的一种案例分 析方法．常用等高条形图来直观反映两个分类变量之间差异的大小； 利用假设检验求随机变量 K2 的值能更精确地判断两个分类变量间的相 关关系． 例 2] 为了解某市市民对政府出台楼市限购令的态度，在该市随 机抽取了 50 名市民进行调查，他们月收入(单位：百元)的频数分布及 对楼市限购令的赞成人数如下表所示： 月收入 15，25) 25，35) 35，45) 45，55) 55，65) 65，75) 频数 5 10 15 10 5 5 赞成 人数 4 8 8 5 2 1 将月收入不低于 55 的人群称为“高收入族”，有收入低于 55 的 人群称为“非高收入族”． (1)已知：K2＝ （a＋b＋c＋d）（ad－bc）2 （a＋b）（c＋d）（a＋c）（b＋d），当 K2＜2.706 时， 没有充分的证据判定赞不赞成楼市限购令与收入高低有关；当 K2＞ 2.706 时，有 90%的把握判断赞成楼市限购令与收入高低有关；当 K2 ＞3.841，有 95%的把握判断定赞不赞成楼市限购令与收入高低有关； 当 K2＞6.635 时，有 99%的把握判定赞不赞成楼市限购令与收入高低 有关． 根据已知条件完成下面的 2×2 列联表，有多大的把握认为赞不赞 成楼市限购令与收入高低有关？ 分类 非高收入族 高收入族 总计 赞成 不赞成 总计 (2)现从月收入在 55，65)的人群中随机抽取两人，求所抽取的两人 中至少一人赞成楼市限购令的概率． 解：(1)2×2 列联表如下表所示： 分类 非高收入族 高收入族 总计 赞成 25 3 28 不赞成 15 7 22 总计 40 10 50 K2＝50（25×7－15×3）2 40×10×22×28 ≈3.43，故有 90%的把握认为楼市限购 令与收入高低有关． (2)设“从月收入在 55，65)的 5 人中随机抽取 2 人，其中至少有 1 人赞成楼市限购令”为事件 A，则事件 A 含有基本事件数为 C25－C23＝ 7，从 5 人中任取 2 人所含基本事件数为 C25＝10，因此所求概率为 7 10. 归纳升华 (1)判断两个分类变量之间是否有关系可以通过等高条形图作粗略 判断，需要确知所作判断犯错误的概率情况下，可进行独立性检验， 独立性检验可以得到较为可靠的结论． (2)独立性检验的一般步骤： ①根据样本数据制成 2×2 列联表； ②根据公式计算 K2 的值； ③比较 K2 与临界值的大小关系，做出统计推断． 变式训练] 调查某医院某段时间内婴儿出生的时间与性别的关 系，得到如下数据．试问能以多大把握认为婴儿的性别与出生时间有 关系？ 性别 晚上 白天 总计 男婴 24 31 55 女婴 8 26 34 总计 32 57 89 解：由公式 K2＝ （a＋b＋c＋d）（ad－bc）2 （a＋b）（c＋d）（a＋c）（b＋d）计算得 K2＝89×（24×26－8×31）2 55×34×32×57 ≈3.69， 由于 K2＞2.706，所以只有 90%的把握说明婴儿出生的时间与性别 有关，故婴儿的出生的时间与性别是相互独立的(也可以说没有充分的 证据显示婴儿的性别与其出生时间有关)． 专题三 数形结合思想 数形结合思想在统计中的应用主要是将收集到的数据利用图表的 形式表示出来，直观地反映变量间的关系． 例 3] 为了解铅中毒病人是否有尿棕色素增加现象，分别对病人 组和对照组的尿液作尿棕色素定性检查，结果如下，问铅中毒病人和 对照组的尿棕色素阳性数有无差别？ 组别 阳性数 阴性数 总计 铅中毒病人 29 7 36 对照组 9 28 37 总计 38 35 73 解： 由上述列联表可知，在铅中毒病人中尿棕色素为阳性的占 80.56%，而对照组仅占 24.32%.说明他们之间有较大差别． 根据列联表作出等高条形图由图可知，铅中毒病人中与对照组相 比较，尿棕色素为阳性差异明显，因此铅中毒病人与尿棕色素为阳性 存在关联关系． 归纳升华 收集数据、整理数据是统计知识处理问题的两个基本步骤，将收 集到的数据利用图表的形式整理出来，能够直观地反映变量之间的关 系．在精确度要求不高的情况下，可以利用散点图、等高条形图等对 两个变量之间的关系做出判断． 变式训练] 根据如下样本数据： x 3 4 5 6 7 8 y 4.0 2.5 －0.5 0.5 －2.0 －3.0 得到的回归方程为y ^＝bx＋a，则( ) A．a＞0，b＞0 B．a＞0，b＜0 C．a＜0，b＞0 D．a＜0，b＜0 解析：根据题中表内数据画出散点图如图所示，由散点图可知 b ＜0，a＞0. 答案： B