数学北师大版（2019）必修第二册：阶段提升课 第二课　三角函数的图象与性质 学案与作业 12页

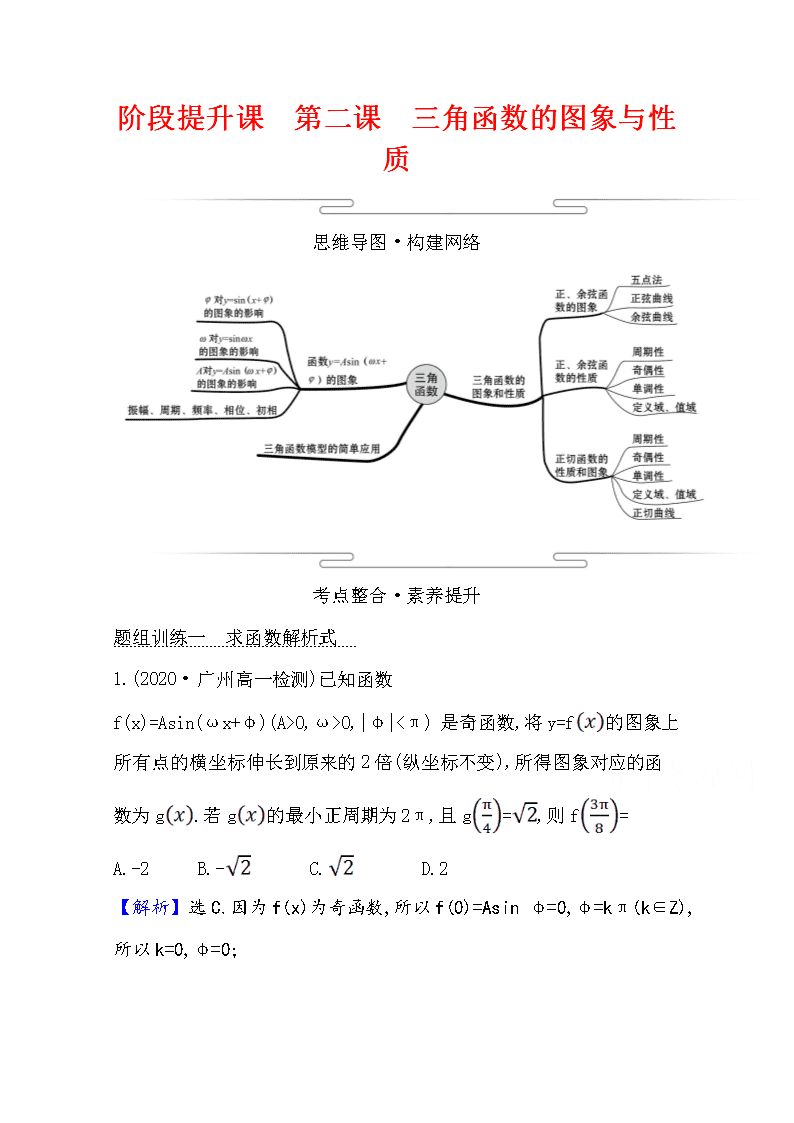
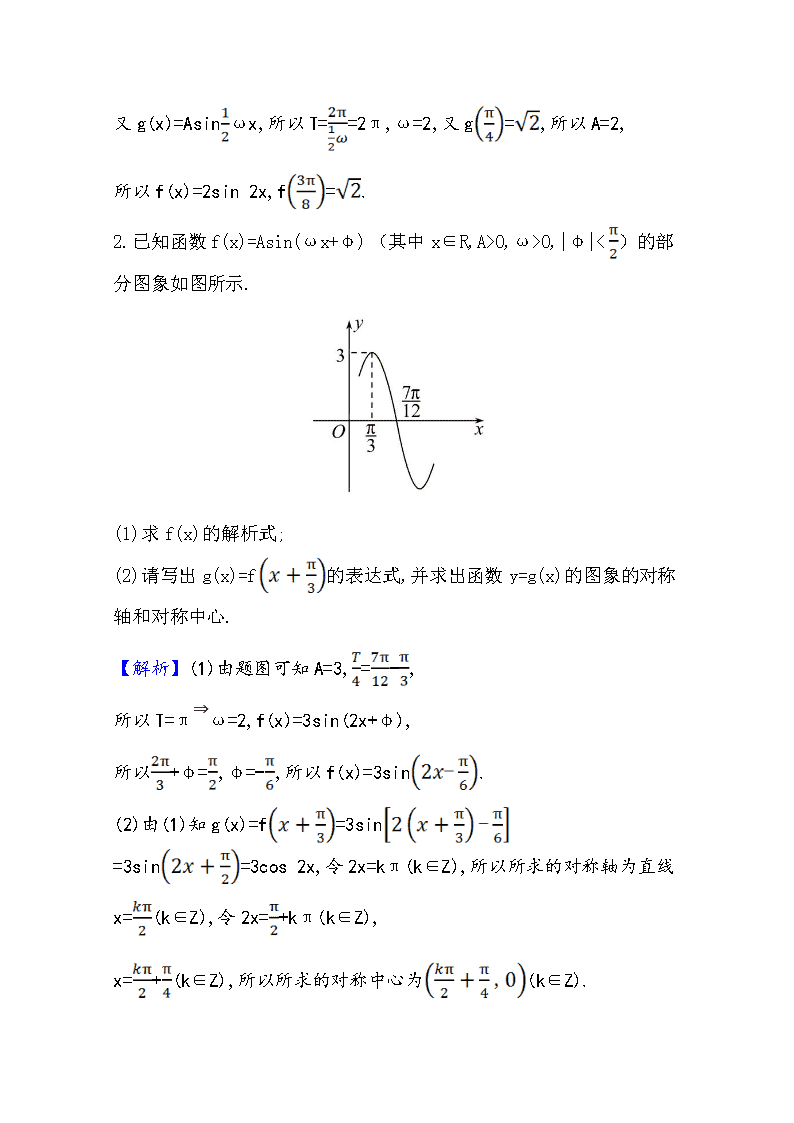
阶段提升课 第二课 三角函数的图象与性 质 思维导图·构建网络 考点整合·素养提升 题组训练一 求函数解析式 1.(2020·广州高一检测)已知函数 f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)是奇函数,将 y=f 的图象上 所有点的横坐标伸长到原来的 2 倍(纵坐标不变),所得图象对应的函数 为 g .若 g 的最小正周期为 2π,且 g = ,则 f = ( ) A.-2 B.- C. D.2 【解析】选 C.因为 f(x)为奇函数,所以 f(0)=Asin φ=0,φ=kπ(k∈Z), 所以 k=0,φ=0; 又 g(x)=Asin ωx,所以 T= =2π,ω=2,又 g = ,所以 A=2, 所以 f(x)=2sin 2x,f = . 2.已知函数 f(x)=Asin(ωx+φ)（其中 x∈R,A>0,ω>0,|φ|< ）的部 分图象如图所示. (1)求 f(x)的解析式; (2)请写出 g(x)=f 的表达式,并求出函数 y=g(x)的图象的对称 轴和对称中心. 【解析】(1)由题图可知 A=3, = - , 所以 T=π⇒ω=2,f(x)=3sin(2x+φ), 所以 +φ= ,φ=- ,所以 f(x)=3sin . (2)由(1)知 g(x)=f =3sin =3sin =3cos 2x,令 2x=kπ(k∈Z),所以所求的对称轴为直线 x= (k∈Z),令 2x= +kπ(k∈Z), x= + (k∈Z),所以所求的对称中心为 (k∈Z). 由已知条件确定函数 y=Asin(ωx+φ)的解析式,需要确定 A,ω,φ,其 中 A,ω易求,下面介绍求φ的几种方法. (1)平衡点法 由 y=Asin(ωx+φ)=Asin 知它的平衡点的横坐标为- . (2)确定最值法 这种方法避开了“伸缩变换”且不必牢记许多结论,只需解一个特殊 的三角方程. (3)利用单调性 将函数 y=Asin(ωx+φ)的图象与 y=sin x 的图象比较,选取它们的某一 个单调区间得到一个等式,解答即可求出φ. 题组训练二 三角函数图象变换问题 1.(2020·大连高一检测)函数 f =Asin ,其中 的图象如图所示,为了得到 f 的图象,则只需将 g =sin 2x 的图象 ( ) A.向右平移 个长度单位 B.向左平移 个长度单位 C.向右平移 个长度单位 D.向左平移 个长度单位 【解析】选 D.由三角函数 f 的图象可知,A=1 且 = - = ,即 T=π, 又由 T= =π,解得 w=2,即 f =sin(2x+φ), 又由 f =sin =sin =-1, 解得 +φ= +2kπ,k∈Z, 即φ= +2kπ,k∈Z,又由 < , 所以φ= ,即 f =sin , 故将函数 g =sin 2x 的图象向左平移 个长度单位, 即可得到 f =sin =sin 的图象. 2.函数 f =2sin 的图象向右平移 个单位长度,得到的图 象关于 y 轴对称,则 的最小值为 ( ) A. B. C. D. 【解析】选 B.函数 f =2sin 的图象向右平移 个单位长度 得到:f(x)=2sin 的图象关于 y 轴对称,即函数为偶函数, 故φ- =kπ- ⇒φ=kπ- ,所以 的最小值为 . 3.将函数 y=2sin 的图象向右平移 个周期后,所得图象对应 的函数为 ( ) A.y=2sin B.y=2sin C.y=2sin D.y=2sin 【解析】选 D.函数 y=2sin 的周期为π,将函数 y=2sin 的图象向右平移 个周期即 个单位长度, 所得图象对应的函数为 y=2sin =2sin . 对称变换 (1)y=f(x)的图象 y=-f(x)的图象 (2)y=f(x)的图象 y=f(-x)的图象 (3)y=f(x)的图象 y=-f(-x)的图象 题组训练三 三角函数的性质 1.(2020·长沙高一检测)函数 y=sin 是 ( ) A.周期为π的奇函数 B.周期为π的偶函数 C.周期为 2π的奇函数 D.周期为 2π的偶函数 【解析】选 B.设 y=f(x)=sin ,由 y=sin =cos 2x,则 函数的最小正周期为 T= =π,又 f(-x)=cos(-2x)=cos 2x=f ,所以 f 为偶函数. 2.(2020·宜宾高一检测)三角函数值 sin 1,sin 2,sin 3 的大小顺序 是 ( ) A.sin 1>sin 2>sin 3 B.sin 2>sin 1>sin 3 C.sin 1>sin 3>sin 2 D.sin 3>sin 2>sin 1 【解析】选 B.因为 1 弧度≈57°,2 弧度≈114°,3 弧度≈171°,所以 sin 1≈sin 57°,sin 2≈sin 114°=sin 66°, sin 3≈171°=sin 9°. 因为 y=sin x 在 0°sin 1>sin 3. 3.(2020·哈尔滨高一检测)设函数 f(x)=Asin(ωx+φ) 的图象关于直线 x= 对称,它的最小正周期为π,则 ( ) A.f(x)的图象过点 B.f(x)在 上单调递减 C.f(x)的一个对称中心是 D.f(x)的一个对称中心是 【解析】选 C.由题意可得 =π, 所以ω=2,可得 f(x)=Asin(2x+φ). 再由函数图象关于直线 x= 对称, 得 f =Asin =±A,故可取φ= . 故函数 f(x)=Asin . 令 2kπ+ ≤2x+ ≤2kπ+ ,k∈Z,求得 kπ+ ≤x≤kπ+ ,k∈Z,故函 数的减区间为 ,k∈Z,故选项 B 不正确.由于 A 不确 定,故选项 A 不正确.令 2x+ =kπ,k∈Z,可得 x= - ,k∈Z,故函数的 对称中心为 ,k∈Z,故选项 C 正确,选项 D 不正确. 4.函数 y=tan ,x∈ 的值域是______. 【解析】由 x∈ ,所以 + ∈ 结合正切函数的性质可得:10,b 为常数)的函数的单调区间,可以借助于正弦函数、余弦函 数的单调区间,通过解不等式求得. (2)具体求解时注意两点:①要把ωx+φ看作一个整体,若ω<0,先用诱 导公式将式子变形,将 x 的系数化为正;②在 A>0,ω>0 时,将 “ωx+φ”代入正弦(或余弦)函数的单调区间,可以解得与之单调性 一致的单调区间;当 A<0,ω>0 时,用同样方法可以求得与正弦(余弦)函 数单调性相反的单调区间. 题组训练四 三角函数的实际应用 1.(2020·重庆高一检测)如图,重庆欢乐谷的摩天轮被称为“重庆之 眼”,其旋转半径为 50 米,最高点距离地面 120 米,开启后按逆时针方 向旋转,旋转一周大约 18 分钟.将摩天轮看成圆面,在该平面内,以过摩 天轮的圆心且垂直于地平面的直线为 y 轴,该直线与地平面的交点为坐 标原点建立平面直角坐标系,某人在最低点的位置坐上摩天轮的座舱, 摩天轮开始启动,并记该时刻为 t=0,则此人距离地面的高度 f(t)与摩 天轮运行时间 t(单位:分钟)的函数关系式为 ( ) A.f(t)=50sin t+20(t≥0) B.f(t)=50sin +70(t≥0) C.f(t)=50sin +20(t≥0) D.f(t)=50sin +70(t≥0) 【解析】选 B.设 f(t)=Asin(ωt+φ)+B , ⇒ ,T=18,ω= = , 当 t=0 时 sin φ=-1,φ=- , f(t)=50sin +70(t≥0). 2.(2020·北京高一检测)某城市一年中 12 个月的平均气温与月份的关 系可近似地用三角函数 y=Acos +B 来表示. 已知 6 月份的月平均气温最高,为 28℃,12 月份的月平均气温最低,为 18℃,则 10 月份的月平均气温为________℃. 【解析】根据题意得 28=A+B,18=-A+B, 解得 A=5,B=23,所以 y=23+5cos ,令 x=10 得 y=23+5cos =23+5cos =20.5. 答案:20.5 3.(2020·宁波高一检测)在自然条件下,对某种细菌在一天内存活的 时间进行了一年的统计与测量,得到 10 次测量结果(时间近似到 0.1 小 时),结果如表所示: 日期 1 月 1 日 2 月 28 日 3 月 21 日 4 月 27 日 5 月 6 日 6 月 21 日 8 月 13 日 9 月 20 日 10 月 25 日 12 月 21 日 日期位置 序号 x 1 59 80 117 126 172 225 263 298 355 存活时间 y 小时 5.6 10. 2 12. 4 16. 4 17. 3 19. 4 16. 4 12. 4 8.5 5.4 (1)试选用一个形如 y=Asin(ωx+φ)+t 的函数来近似描述一年(按 365 天计)中该细菌一天内存活的时间 y 与日期位置序号 x 之间的函数 解析式. (2)用(1)中的结果估计该种细菌一年中大约有多少天的存活时间大于 15.9 小时. 【解析】(1)细菌存活时间与日期位置序号 x 之间的函数解析式满足 y=Asin(ωx+φ)+t,由表格可知函数的最大值为 19.4,最小值为 5.4,所 以 19.4-5.4=14,故 A=7. 又 19.4+5.4=24.8,故 t=12.4. 又 T=365,所以ω= .当 x=172 时, +φ= , 所以φ=- , 所以 y=7sin +12.4(1≤x≤365,x∈N). (2)由 y>15.9 得 sin > , 所以 < x- < ,可得 111.17