2021届高考数学一轮总复习课时作业64几何概型含解析苏教版 8页

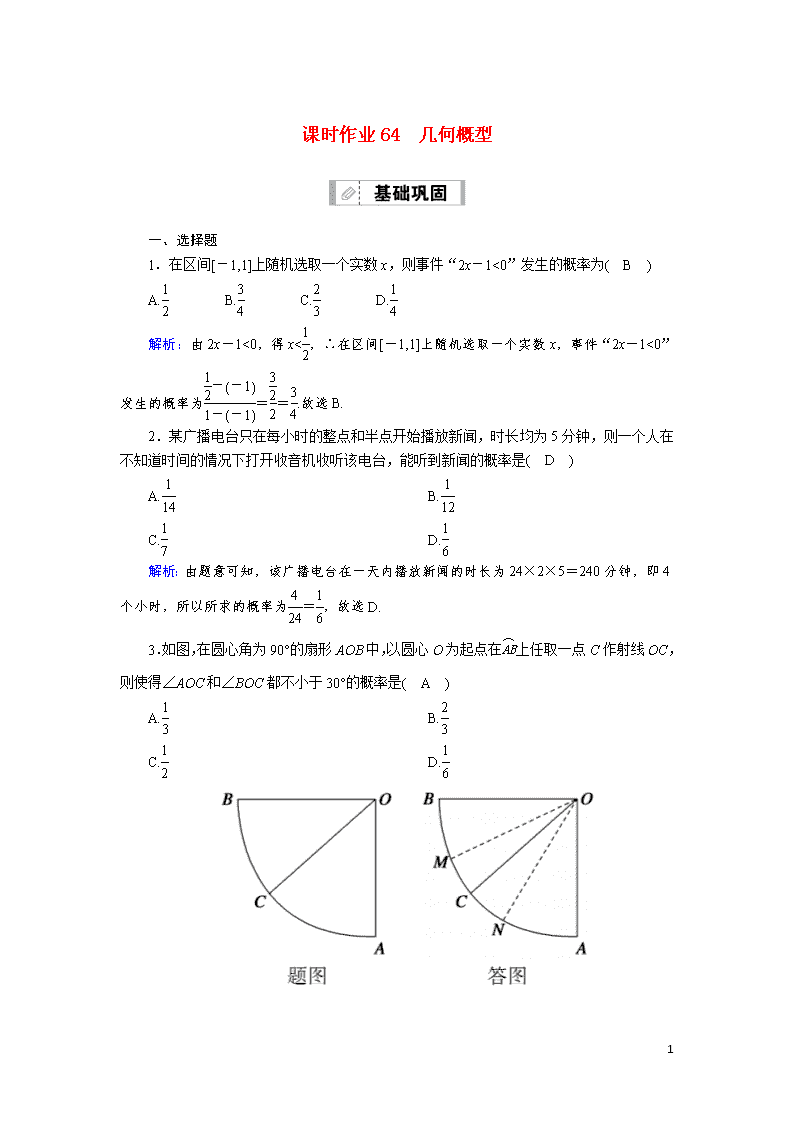
课时作业64　几何概型 一、选择题 ‎1．在区间[－1,1]上随机选取一个实数x，则事件“2x－1<0”发生的概率为(　B　)‎ A.　　　　B.　　　　C.　　　　D. 解析：由2x－1<0，得x<，∴在区间[－1,1]上随机选取一个实数x，事件“2x－1<0”发生的概率为＝＝.故选B.‎ ‎2．某广播电台只在每小时的整点和半点开始播放新闻，时长均为5分钟，则一个人在不知道时间的情况下打开收音机收听该电台，能听到新闻的概率是(　D　)‎ A. B. C. D. 解析：由题意可知，该广播电台在一天内播放新闻的时长为24×2×5＝240分钟，即4个小时，所以所求的概率为＝，故选D.‎ ‎3．如图，在圆心角为90°的扇形AOB中，以圆心O为起点在上任取一点C作射线OC，则使得∠AOC和∠BOC都不小于30°的概率是(　A　)‎ A. B. C. D. 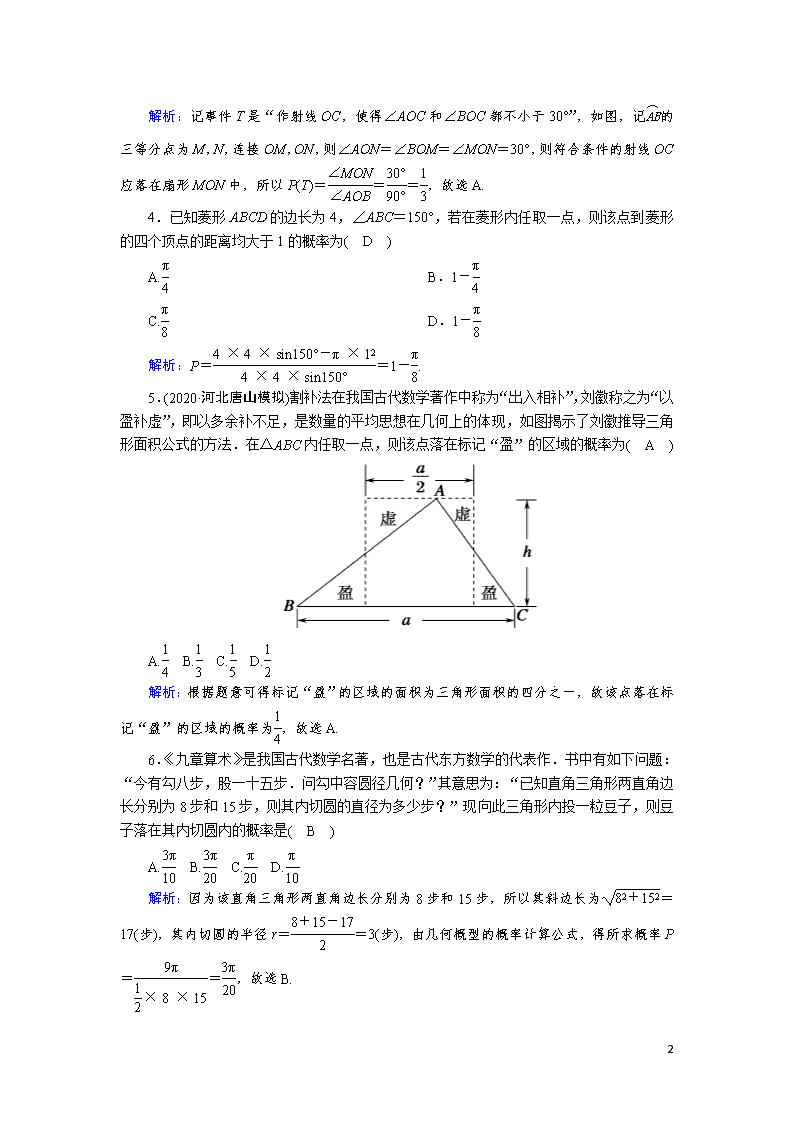解析：记事件T是“作射线OC，使得∠AOC和∠BOC都不小于30°”，如图，记 8‎ 的三等分点为M，N，连接OM，ON，则∠AON＝∠BOM＝∠MON＝30°，则符合条件的射线OC应落在扇形MON中，所以P(T)＝＝＝，故选A.‎ ‎4．已知菱形ABCD的边长为4，∠ABC＝150°，若在菱形内任取一点，则该点到菱形的四个顶点的距离均大于1的概率为(　D　)‎ A. B．1－ C. D．1－ 解析：P＝＝1－.‎ ‎5．(2020·河北唐山模拟)割补法在我国古代数学著作中称为“出入相补”，刘徽称之为“以盈补虚”，即以多余补不足，是数量的平均思想在几何上的体现，如图揭示了刘徽推导三角形面积公式的方法．在△ABC内任取一点，则该点落在标记“盈”的区域的概率为(　A　)‎ A. B. C. D. 解析：根据题意可得标记“盈”的区域的面积为三角形面积的四分之一，故该点落在标记“盈”的区域的概率为，故选A.‎ ‎6．《九章算术》是我国古代数学名著，也是古代东方数学的代表作．书中有如下问题：“今有勾八步，股一十五步．问勾中容圆径几何？”其意思为：“已知直角三角形两直角边长分别为8步和15步，则其内切圆的直径为多少步？”现向此三角形内投一粒豆子，则豆子落在其内切圆内的概率是(　B　)‎ A. B. C. D. 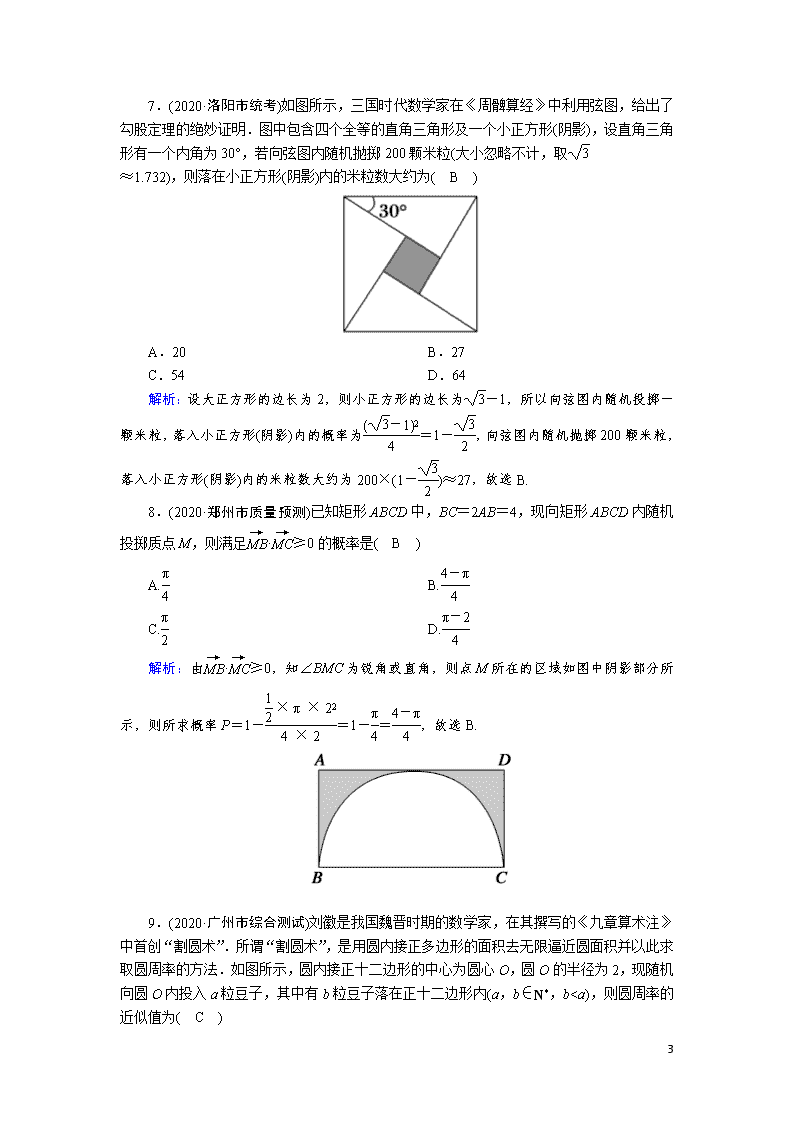解析：因为该直角三角形两直角边长分别为8步和15步，所以其斜边长为＝17(步)，其内切圆的半径r＝＝3(步)，由几何概型的概率计算公式，得所求概率P＝＝，故选B.‎ ‎7．(2020·洛阳市统考)如图所示，三国时代数学家在《周髀算经》中利用弦图，给出了勾股定理的绝妙证明．图中包含四个全等的直角三角形及一个小正方形(阴影)，设直角三角形有一个内角为30°，若向弦图内随机抛掷200颗米粒(大小忽略不计，取 8‎ ‎≈1.732)，则落在小正方形(阴影)内的米粒数大约为(　B　)‎ A．20 B．27‎ C．54 D．64‎ 解析：设大正方形的边长为2，则小正方形的边长为－1，所以向弦图内随机投掷一颗米粒，落入小正方形(阴影)内的概率为＝1－，向弦图内随机抛掷200颗米粒，落入小正方形(阴影)内的米粒数大约为200×(1－)≈27，故选B.‎ ‎8．(2020·郑州市质量预测)已知矩形ABCD中，BC＝2AB＝4，现向矩形ABCD内随机投掷质点M，则满足·≥0的概率是(　B　)‎ A. B. C. D. 解析：由·≥0，知∠BMC为锐角或直角，则点M所在的区域如图中阴影部分所示，则所求概率P＝1－＝1－＝，故选B.‎ ‎9．(2020·广州市综合测试)刘徽是我国魏晋时期的数学家，在其撰写的《九章算术注》中首创“割圆术”．所谓“割圆术”，是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法．如图所示，圆内接正十二边形的中心为圆心O，圆O的半径为2，现随机向圆O内投入a粒豆子，其中有b粒豆子落在正十二边形内(a，b∈N*，b，解得k>1或k<－1，又k∈[－，]，所以－≤k<－1或1