【新教材】2020-2021学年高中人教A版数学必修第二册习题：6-1　平面向量的概念 5页

第六章平面向量及其应用 ‎6.1　平面向量的概念 课后篇巩固提升 基础达标练 ‎1.有下列物理量:①质量;②速度;③力;④加速度;⑤路程;⑥功.其中,不是向量的个数是(　　)‎ ‎　　 　　　　　　　　　　　　　　‎ A.1 B.2‎ C.3 D.4‎ 解析因为速度、力和加速度既有大小,又有方向,所以它们是向量;而质量、路程和功只有大小,没有方向,所以它们不是向量,故不是向量的个数是3.‎ 答案C ‎2.在同一平面上,把向量所在直线平行于某一直线的一切向量的始点放在同一点,那么这些向量的终点所构成的图形是(　　)‎ A.一条线段 B.一条直线 C.圆上一群孤立的点 D.一个半径为1的圆 解析由于向量的起点确定,而向量所在直线平行于同一直线,所以随着向量模的变化,向量的终点构成的是一条直线.‎ 答案B ‎3.‎ 如图所示,在正三角形ABC中,P,Q,R分别是AB,BC,AC的中点,则与向量相等的向量是(　　)‎ A.‎ B.‎ C.‎ D.‎ 解析向量相等要求模相等,方向相同,因此都是和相等的向量.‎ 答案B ‎4.若||=||且,则四边形ABCD的形状为(　　)‎ A.正方形 B.矩形 C.菱形 D.等腰梯形 解析由知,AB=CD且AB∥CD,即四边形ABCD为平行四边形.又因为||=||,所以四边形ABCD为菱形.‎ 答案C ‎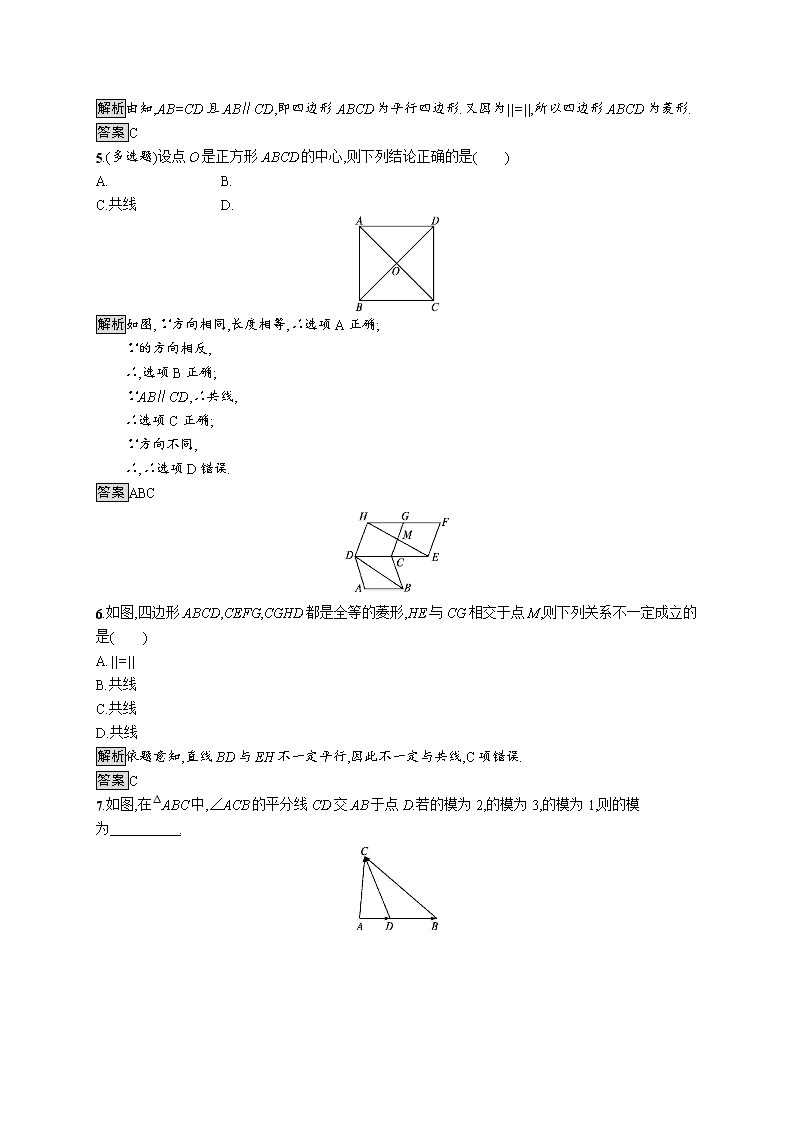5.(多选题)设点O是正方形ABCD的中心,则下列结论正确的是(　　)‎ A. B.‎ C.共线 D.‎ 解析如图,∵方向相同,长度相等,∴选项A正确;‎ ‎∵的方向相反,‎ ‎∴,选项B正确;‎ ‎∵AB∥CD,∴共线,‎ ‎∴选项C正确;‎ ‎∵方向不同,‎ ‎∴,∴选项D错误.‎ 答案ABC ‎6.如图,四边形ABCD,CEFG,CGHD都是全等的菱形,HE与CG相交于点M,则下列关系不一定成立的是(　　)‎ A.||=||‎ B.共线 C.共线 D.共线 解析依题意知,直线BD与EH不一定平行,因此不一定与共线,C项错误.‎ 答案C ‎7.如图,在△ABC中,∠ACB的平分线CD交AB于点D.若的模为2,的模为3,的模为1,则的模为　　　　　. ‎ 解析如图,延长CD,过点A作BC的平行线交CD的延长线于点E.‎ 因为∠ACD=∠BCD=∠AED,‎ 所以||=||.‎ 因为△ADE∽△BDC,‎ 所以,‎ 故||=.‎ 答案 ‎8.‎ 如图所示,4×3的矩形(每个小方格都是单位正方形),在起点和终点都在小方格的顶点处的向量中,试问:‎ ‎(1)与相等的向量共有几个?‎ ‎(2)与平行且模为的向量共有几个?‎ ‎(3)与方向相同且模为3的向量共有几个?‎ 解(1)与向量相等的向量共有5个(不包括本身).‎ ‎(2)与向量平行且模为的向量共有24个.‎ ‎(3)与向量方向相同且模为3的向量共有2个.‎ 能力提升练 ‎1.(2020成都高一检测)已知a为单位向量,下列说法正确的是(　　)‎ A.a的长度为一个单位长度 B.a与0不平行 C.单位向量都相等 D.a与0不是平行向量 解析∵已知a为单位向量,∴a的长度为一个单位长度,故A正确;‎ ‎∴a与0平行,故B错误;‎ 由于单位向量的方向是任意的,故C错误;零向量与任何向量都是平行向量,故D错误.‎ 答案A ‎2.(多选题)如图,在菱形ABCD中,∠DAB=120°,则以下说法正确的是(　　)‎ A.与相等的向量只有一个(不包括本身)‎ B.与的模相等的向量有9个(不包括本身)‎ C.的模为模的倍 D.不共线 解析A项,由相等向量的定义知,与相等的向量只有,故A正确;B项,因为AB=BC=CD=DA=AC,所以与的模相等的向量除外有9个,故B正确;C项,在Rt△ADO中,∠DAO=60°,则DO=DA,所以BD=DA,故C正确;D项,因为四边形ABCD是菱形,所以共线,故D错误.‎ 答案ABC ‎3.给出下列四个条件:①a=b;②|a|=|b|;③a与b方向相反;④|a|=0或|b|=0.其中能使a∥b成立的条件是　　　　　.(填序号) ‎ 解析若a=b,则a与b大小相等且方向相同,所以a∥b;若|a|=|b|,则a与b的大小相等,而方向不确定,因此不一定有a∥b;方向相同或相反的向量都是平行向量,因此若a与b方向相反,则有a∥b;零向量与任意向量平行,所以若|a|=0或|b|=0,则a∥b.‎ 答案①③④‎ ‎4.如图,四边形ABCD和ABDE都是边长为1的菱形,已知下列说法:‎ ‎①都是单位向量;‎ ‎②;‎ ‎③与相等的向量有3个(不包括本身);‎ ‎④与共线的向量有3个(不包括本身);‎ ‎⑤与向量大小相等、方向相反的向量为.‎ 其中正确的是　　　　　　　　.(填序号) ‎ 解析①由两菱形的边长都为1,故①正确;②正确;③与相等的向量是,故③错误;④与共线的向量是,故④正确;⑤正确.‎ 答案①②④⑤‎ ‎5.已知在四边形ABCD中,,且||=||,tan D=,判断四边形ABCD的形状.‎ 解∵在四边形ABCD中,,‎ ‎∴AB