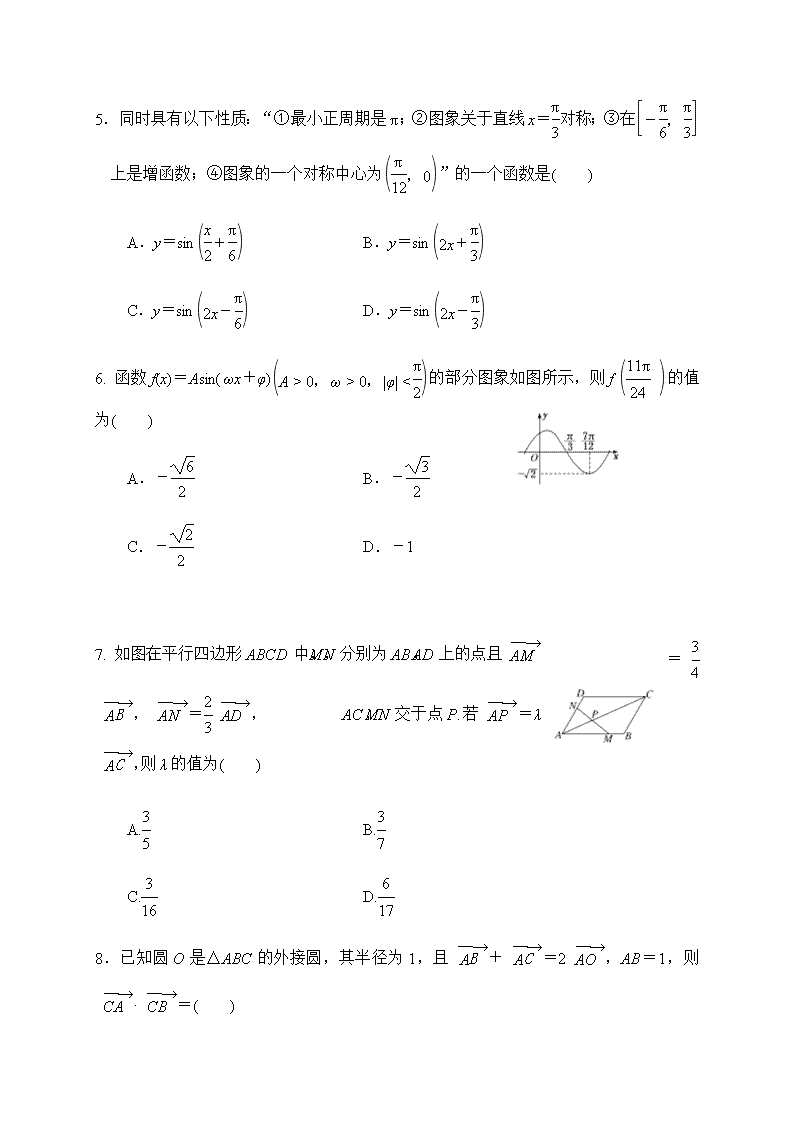河南省洛阳市第一高级中学2021届高三上学期10月月考数学（文）试题 Word版含答案 13页

洛阳一高2020-2021学年第一学期高三年级10月月考文科数学试卷 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．已知a为实数，若复数z＝(a2－1)＋(a＋1)i为纯虚数，则＝(　　)‎ A．1 B．0‎ C．1＋i D．1－i ‎2.下列命题中错误的是 ‎ 命题“若，则”的逆否命题是真命题 命题“”的否定是“”‎ 若为真命题，则为真命题 使“”是“”的必要不充分条件 ‎ ‎3．已知定义在R上的奇函数f(x)有f＋f(x)＝0，当－≤x≤0时，f(x)＝2x＋a，则f(16)的值为(　　)‎ A. B．－ C. D．－ ‎4．已知等比数列{an}的前n项和为Sn，且a1＋a3＝，a2＋a4＝，则＝(　　)‎ A．4n－1　　　　　　　　　　 B．4n－1‎ C．2n－1 D．2n－1‎ ‎5．同时具有以下性质：“①最小正周期是π；②图象关于直线x＝对称；③在上是增函数；④图象的一个对称中心为”的一个函数是(　　)‎ A．y＝sin B．y＝sin C．y＝sin D．y＝sin 6. 函数f(x)＝Asin(ωx＋φ)的部分图象如图所示，则f的值为(　　)‎ A．－　　　　　　　　 　B．－ C．－ D．－1‎ 7. 如图，在平行四边形ABCD中，M，N分别为AB，AD上的点，且＝，＝， AC，MN交于点P.若＝λ，则λ的值为(　　)‎ A. B. C. D. ‎8．已知圆O是△ABC的外接圆，其半径为1，且＋＝2，AB＝1，则·＝(　　)‎ A. B．3 C. D．2 ‎9 .已知函数f(x)＝ex－，其中e是自然对数的底数，则关于x的不等式f(2x－1)＋f(－x－1)>0的解集为(　　)‎ A.∪(2，＋∞) B．(2，＋∞)‎ C.∪(2，＋∞) D．(－∞，2)‎ ‎10．若一直线与曲线y＝和曲线x2＝ay(a>0)相切于同一点P，则a的值为(　　)‎ A.2e B．3‎ C. D．2 ‎11．在△ABC中，角A，B，C的对边分别为a，b，c.若2cos2－cos 2C＝1,4sin B＝3sin A，a－b＝1，则c的值为(　　)‎ A. B. C. D．6‎ ‎12．在△ABC中，角A，B，C所对的边分别为a，b，c，若bc＝1，b＋2ccos A＝0，则当角B取得最大值时，△ABC的周长为(　　)‎ A．2＋ B．2＋ C．3 D．3＋ 二、填空题：本大题共4个小题，每小题5分，共20分。‎ ‎13．已知向量＝(k,12)，＝(4,5)，＝(10，k)，且A，B，C三点共线，当k<0时，若k为直线的斜率，则过点(2，－1)的直线方程为________．‎ 14. 已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，它的终边过点P ‎.若角β满足sin(α＋β)＝，则cos β的值为________．‎ ‎15.已知f(x)为偶函数，当x≥0时，f(x)＝则不等式f(x－1)≤的解集为________．‎ ‎16．已知函数f(x)＝若f(x)在区间[m, 4]上的值域为[－1,2]，则实数m的取值范围为________．‎ ‎ ‎ 三、解答题：共70分。解答应写出文字说明、证明过程或演算步骤。第17～21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎17．（本小题满分12分）‎ 如图,是直角斜边上一点,．‎ ‎(1)若，求角的大小；‎ ‎(2)若，且，求的长．‎ ‎18．（本小题满分12分）‎ 已知为数列的前n项和.已知，.‎ ‎(1)求的通项公式；‎ ‎(2)设，求数列的前n项和.‎ ‎19.（本小题满分12分）‎ ‎ 已知向量.‎ ‎ (1)求的最大值及取得最大值时的取值集合；‎ ‎ (2)在中，是角的对边，若且，求周长的取值范围.‎ ‎20．（本小题满分12分）‎ 已知函数．‎ ‎(1)若函数在上是减函数，求实数的取值范围；‎ ‎(2)令，是否存在实数，当是自然常数)时，函数的最小值是3，若存在，求出的值；若不存在，说明理由.‎ ‎21．（本小题满分12分）‎ ‎ 已知函数．‎ ‎（1）当a＜1时，讨论函数f（x）的单调性；‎ ‎（2）若不等式对于任意x∈[e﹣1，e]成立，求正实数a的取值范围．‎ 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分．作答时，‎ 请用2B铅笔在答题卡上，将所选题号对应的方框涂黑.‎ ‎22．（本小题满分10分）选修4-4：极坐标和参数方程选讲 在平面直角坐标系中，直线的参数方程为(为参数)，圆的方程为 ‎.以原点为极点，轴正半轴为极轴建立极坐标系.‎ ‎(1)求直线及圆的极坐标方程；‎ ‎(2)若直线与圆交于两点，求的值.‎ ‎23．（本小题满分10分）选修4-5：不等式选讲 已知函数．‎ ‎(1)解不等式；‎ ‎(2)设函数的最小值为，实数满足，求证：.‎ 已知函数，为不等式的解集.‎ 高三10月月考文科数学参考答案 一、选择题：1-5 DBCDC 6-10 DDBBA 11-12 AA ‎ 二、填空题：13. 2x＋y－3＝0 14. －或 ‎ 15.∪ 16.[－8，－1]‎ 三、解答题 ‎17.(1)在中,根据正弦定理,有. ……1分 因为,所以. ……3分 又 ‎ 所以. ……5分 于是,‎ 所以. ……6分 ‎（2）设,则,,. ……7分 于是,, ……9分 在中,由余弦定理,得 ‎,‎ 即, ……11分 得，故 ． ……12分 ‎18.(1),,‎ ‎ , ……2分 即. ……3分 ‎,.‎ 又， ,(舍去), ……5分 是首为3，公差为2的等差数列，通项公式为. ……6分 ‎(2)由,得. ……9分 设数列的前n项和为，则 ‎. ……12分 ‎19.解：(1),‎ ‎ ……2分 ‎， ……3分 的最大值为， ……4分 此时，即， ……5分 ‎. ……6分 ‎(2) . ……7分 ‎,. ……8分 ‎ ……9分 ‎, ……10分 ‎.‎ ‎,,即周长的取值范围是. ……12分 ‎20.解：(1)在上恒成立， ……2分 令，有得， ……4分 得，所以的取值范围是. ……5分 ‎(2)假设存在实数，使有最小值3，‎ ‎. ……6分 ① 当时，在上单调递减， ‎ ‎（舍去）. ……8分 ② 当时，在上单调递减，在上单调递增 ‎∴，满足条件． ……10分 ③ 当时，在上单调递减，‎ ‎（舍去）， ……11分 综上，存在实数，使得当时有最小值3． ……12分 ‎21．已知函数．‎ ‎（1）当a＜1时，讨论函数f（x）的单调性；‎ ‎（2）若不等式对于任意x∈[e﹣1，e]成立，求正实数a的取值范围．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）函数f（x）的定义域为（0，+∞），‎ f′（x）＝x﹣（a+1）+＝，---------------------------------------2分 若0＜a＜1，‎ 当0＜x＜a或x＞1时，f′（x）＞0，f（x）单调递增；‎ 当a＜x＜1时，f′（x）＜0，f（x）单调递减，--------------------------------3分 若a≤0，‎ 当0＜x＜1时，f′（x）＜0，f（x）单调递减；‎ 当x＞1时，f′（x）＞0，f（x）单调递增．-------------------------------------4分 综上所述，当a≤0时，函数f（x）在（1，+∞）上单调递增，在（0，1）上单调递减；‎ 当0＜a＜1时，函数f（x）在（a，1）上单调递减，在（0，a）和（1，+∞）上单调递增．---5分 ‎（2）原题等价于对任意x∈[，e]，有﹣alnx+xa≤e﹣1成立，--------------6分 设g（x）＝﹣alnx+xa，a＞0，所以g（x）max≤e﹣1，‎ g′（x）＝，-----------------------------------------------------------------7分 令g′（x）＜0，得0＜x＜1；令g′（x）＞0，得x＞1，‎ 所以函数g（x）在[，1]上单调递减，在（1，e]上单调递增，----------------8分 g（x）max＝max（g（）＝a+e﹣a，g（e）＝﹣a+ea），‎ 设h（a）＝g（e）﹣g（）＝ea﹣e﹣a﹣2a（a＞0），‎ 则h′（a）＝ea+e﹣a﹣2＞2﹣2＝0，‎ 所以h（a）在（0，+∞）上单调递增，‎ 故h（a）＞h（0）＝0，‎ 所以g（e）＞g（），---------------------------------------------------------------------10分 从而g（x）max＝g（e）＝﹣a+ea，‎ 所以﹣a+ea≤e﹣1，即ea﹣a﹣e+1≤0，‎ 设φ（a）＝ea﹣a﹣e+1（a＞0），则φ′（a）＝ea﹣1＞0，‎ 所以φ（a）在（0，+∞）上单调递增，‎ 又φ（1）＝0，所以ea﹣a﹣e+1≤0的解为a≤1，‎ 因为a＞0，所以正实数a的取值范围为（0，1]．----------------------------------12分 ‎22.解：(1)由直线的参数方程，‎ 得其普通方程为， ……2分 ‎∴直线的极坐标方程为. ……3分 又∵圆的方程为，‎ 将代入并化简得， ……4分 ‎∴圆的极坐标方程为. ……5分 ‎(2)将直线：，‎ 与圆：联立，得 ‎， ……6分 整理得，∴. ……8分 不妨记点A对应的极角为，点B对应的极角为，且. ……9分 于是，. ……10分 ‎23. (1)，即.‎ 当时，不等式可化为. ‎ 又∵，∴； ……1分 当时，不等式可化为. ‎ 又∵，∴. ……2分 当时，不等式可化为.‎ 又∵，∴. ……3分 综上所得，，或，即.‎ ‎∴原不等式的解集为. ……5分 ‎(2)由绝对值不等式性质得，，‎ ‎∴，即. ……7分 令，则，，‎ ‎， ……9分 原不等式得证. ……10分