- 66.37 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2.1.2 指数函数及其性质(第一课时)
教学目标:1、理解指数函数的概念
2、根据图象分析指数函数的性质
3、应用指数函数的单调性比较幂的大小
教学重点:指数函数的图象和性质
教学难点:底数a对函数值变化的影响
教学方法:学导式
(一)复习:(提问)
引例1:某种细胞分裂时,由1个分裂成2个,2个分裂成4个……1个这样的细胞分裂次后,得到的细胞个数与的函数关系式是:.
这个函数便是我们将要研究的指数函数,其中自变量作为指数,而底数2是一个大于0且不等于1的常量。
(二)新课讲解:
1.指数函数定义:
一般地,函数(且)叫做指数函数,其中是自变量,函数定义域是.
练习:判断下列函数是否为指数函数。
① ② ③(且)④
⑤ ⑥ ⑦ ⑧.
2.指数函数(且)的图象:
例1.画的图象(图(1)).
解:列出的对应表,用描点法画出图象
…
-3
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
3
…
…
0.13
0.25
0.35
0.5
0.71
1
1.4
2
2.8
4
8
…
图(1)
例2.画的图象(图(1)).
…
-3
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
3
…
…
8
4
2.8
2
1.4
1
0.71
0.5
0.35
0.25
0.13
…
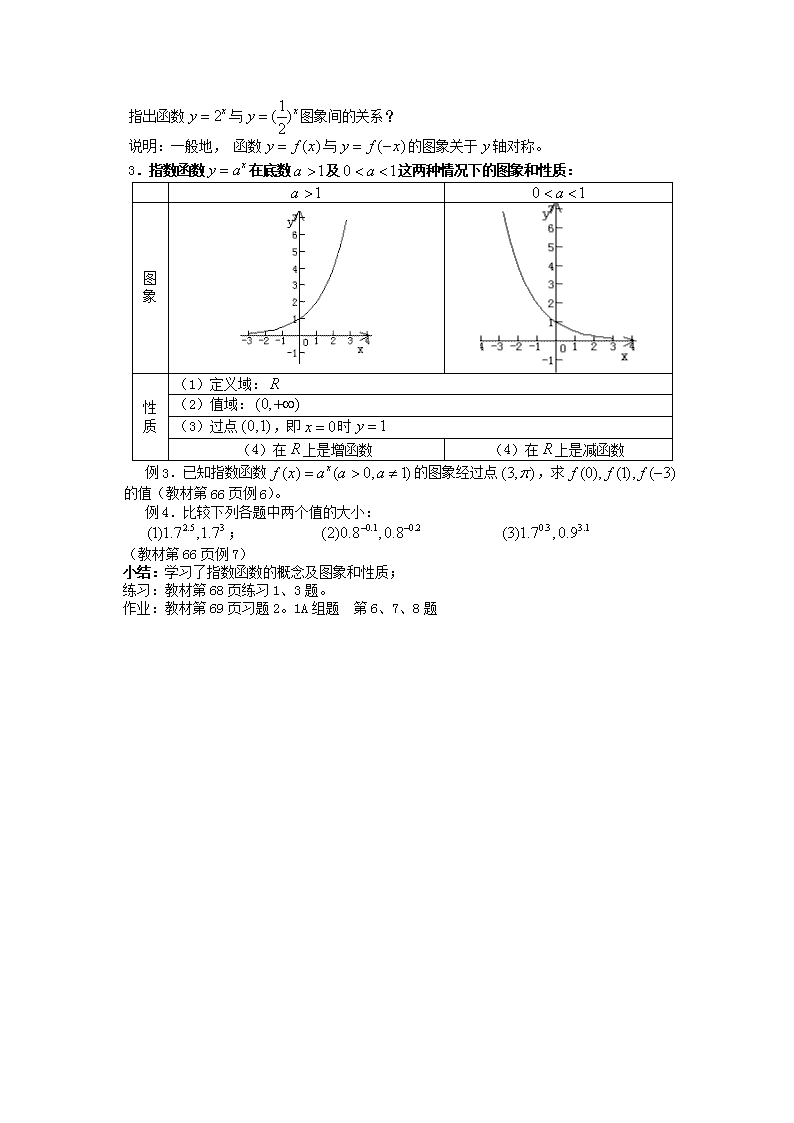
指出函数与图象间的关系?
说明:一般地, 函数与的图象关于轴对称。
3.指数函数在底数及这两种情况下的图象和性质:
图象
性质
(1)定义域:
(2)值域:
(3)过点,即时
(4)在上是增函数
(4)在上是减函数
例3.已知指数函数的图象经过点,求的值(教材第66页例6)。
例4.比较下列各题中两个值的大小:
;
(教材第66页例7)
小结:学习了指数函数的概念及图象和性质;
练习:教材第68页练习1、3题。
作业:教材第69页习题2。1A组题 第6、7、8题
相关文档
- 【数学】2020届一轮复习人教版(理)第2021-06-164页
- 人教A高中数学必修三 分层抽样学案2021-06-164页
- 江苏省七市(南通、泰州、扬州、徐州2021-06-1617页
- 【数学】2019届一轮复习人教A版(文)2021-06-1610页
- 江苏省盐城市一中、射中等五校20202021-06-164页
- 人教版必修三第二章统计2-1-3 分2021-06-164页
- 2021届高考数学一轮总复习第二章函2021-06-1635页
- 【数学】2020届一轮复习人教A版应2021-06-168页
- 人教新课标A版高二数学导数及其应2021-06-1611页
- 人教版高中数学必修二检测:第二章点2021-06-1611页