高中数学人教a版选修4-1章末综合测评1word版含解析 14页

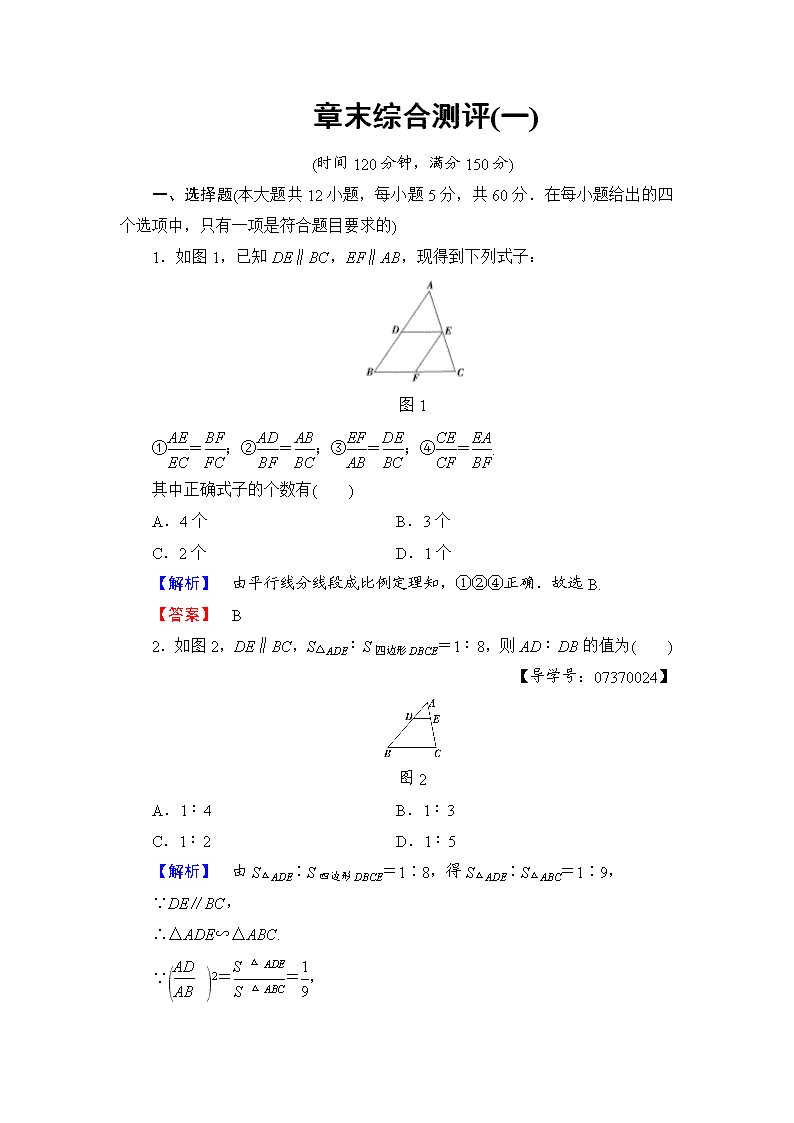
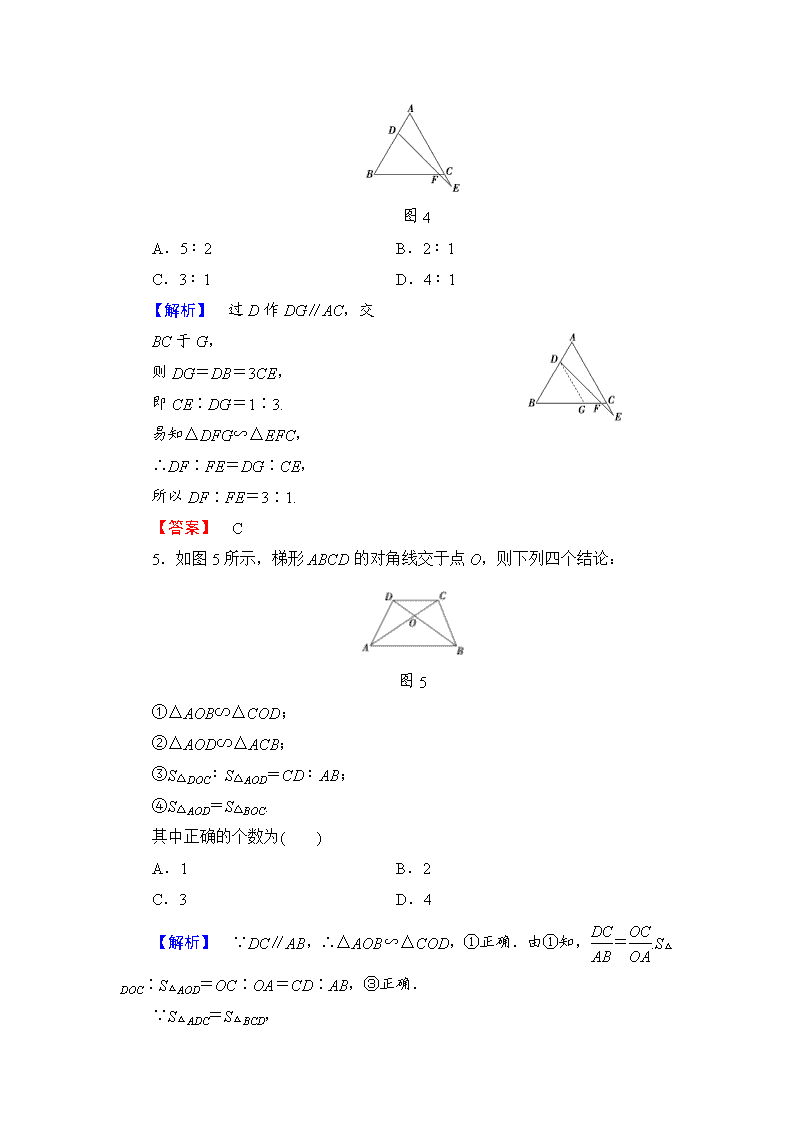
章末综合测评(一) (时间 120 分钟，满分 150 分) 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四 个选项中，只有一项是符合题目要求的) 1．如图 1，已知 DE∥BC，EF∥AB，现得到下列式子： 图 1 ①AE EC ＝BF FC ；②AD BF ＝AB BC ；③EF AB ＝DE BC ；④CE CF ＝EA BF. 其中正确式子的个数有( ) A．4 个 B．3 个 C．2 个 D．1 个 【解析】 由平行线分线段成比例定理知，①②④正确．故选 B. 【答案】 B 2．如图 2，DE∥BC，S△ADE∶S 四边形 DBCE＝1∶8，则 AD∶DB 的值为( ) 【导学号：07370024】 图 2 A．1∶4 B．1∶3 C．1∶2 D．1∶5 【解析】 由 S△ADE∶S 四边形 DBCE＝1∶8，得 S△ADE∶S△ABC＝1∶9， ∵DE∥BC， ∴△ADE∽△ABC. ∵ AD AB 2＝S△ADE S△ABC ＝1 9 ， ∴AD AB ＝1 3 ， ∴AD∶DB＝1∶2. 【答案】 C 3．如图 3 所示，将△ABC 的高 AD 三等分，过每一分点作底面平行线，这 样把三角形分成三部分，则这三部分的面积为 S1，S2，S3，则 S1∶S2∶S3 等于 ( ) 图 3 A．1∶2∶3 B．2∶3∶4 C．1∶3∶5 D．3∶5∶7 【解析】 如图所示，E，F 分别为△ABC 高 AD 的三 等分点，过点 E 作 BC 的平行线交 AB，AC 于点 M，N， 过点 F 作 BC 的平行线交 AB，AC 于点 G，H.△AMN∽△ ABC，S△AMN S△ABC ＝1 9 ，∴S1＝1 9S△ABC. 又△AGH∽△ABC，S△AGH S△ABC ＝4 9 ，S△AGH＝S1＋S2， ∴S1＋S2＝4 9S△ABC， ∴S2＝3 9S△ABC，∴S3＝5 9S△ABC， ∴S1∶S2∶S3＝1∶3∶5，故选 C. 【答案】 C 4．如图 4，在△ABC 中，AB＝AC，D 在 AB 上，E 在 AC 的延长线上，BD ＝3CE，DE 交 BC 于 F，则 DF∶FE 等于( ) 图 4 A．5∶2 B．2∶1 C．3∶1 D．4∶1 【解析】 过 D 作 DG∥AC，交 BC 于 G， 则 DG＝DB＝3CE， 即 CE∶DG＝1∶3. 易知△DFG∽△EFC， ∴DF∶FE＝DG∶CE， 所以 DF∶FE＝3∶1. 【答案】 C 5．如图 5 所示，梯形 ABCD 的对角线交于点 O，则下列四个结论： 图 5 ①△AOB∽△COD； ②△AOD∽△ACB； ③S△DOC∶S△AOD＝CD∶AB； ④S△AOD＝S△BOC. 其中正确的个数为( ) A．1 B．2 C．3 D．4 【解析】 ∵DC∥AB，∴△AOB∽△COD，①正确．由①知，DC AB ＝OC OA.S△ DOC∶S△AOD＝OC∶OA＝CD∶AB，③正确． ∵S△ADC＝S△BCD， ∴S△ADC－S△COD＝S△BCD－S△COD， ∴S△AOD＝S△BOC，④正确． 故①③④正确． 【答案】 C 6．如图 6 所示，铁道口的栏杆短臂长 1 m，长臂长 16 m，当短臂端点下降 0.5 m 时，长臂端点升高( ) 图 6 A．11.25 m B．6.6 m C．8 m D．10.5 m 【解析】 本题是一个实际问题，可抽象为如下数学问 题：如图，等腰△AOC∽等腰△BOD，OA＝1 m，OB＝16 m， 高 CE＝0.5 m，求高 DF.由相似三角形的性质可得 OA∶OB＝ CE∶DF，即 1∶16＝0.5∶DF，解得 DF＝ 8 m. 【答案】 C 7．如图 7 所示，在矩形 ABCD 中，AE⊥BD 于 E，S 矩形＝40 cm2，S△ABE∶S △DBA＝1∶5，则 AE 的长为( ) 图 7 A．4 cm B．5 cm C．6 cm D．7 cm 【解析】 ∵∠BAD＝90°，AE⊥BD， ∴△ABE∽△DBA. ∴S△ABE∶S△DBA＝AB2∶DB2. ∵S△ABE∶S△DBA＝1∶5， ∴AB2∶DB2＝1∶5， ∴AB∶DB＝1∶ 5. 设 AB＝k，DB＝ 5k，则 AD＝2k. ∵S 矩形＝40 cm2，∴k·2k＝40， ∴k＝2 5， ∴BD＝ 5k＝10，AD＝4 5， S△ABD＝1 2BD·AE＝20，即1 2 ×10·AE＝20， ∴AE＝4 cm. 【答案】 A 8．如图 8，把△ABC 沿 AB 边平移到△A′B′C′的位置，它们的重叠部分 (即图中的阴影部分)的面积是 △ABC 的面积的一半，若 AB＝ 2，则此三角形移 动的距离 AA′是( ) 【导学号：07370025】 图 8 A. 2－1 B. 2 2 C．1 D.1 2 【解析】 由题意可知，阴影部分与△ABC 相似，且等于△ABC 面积的1 2 ， ∴A′B∶AB＝ 1 2 ＝1∶ 2. 又∵AB＝ 2，∴A′B＝1， ∴AA′＝ 2－1. 【答案】 A 9．如图 9 所示，在 Rt△ABC 中，∠A＝30°，∠C＝90°，CD⊥AB 于 D，则 BD∶AD＝( ) 图 9 A.1 3 B.1 4 C.2 3 D.2 5 【解析】 设 CD＝ 3，则 AD＝3，BD＝1，∴BD AD ＝1 3. 【答案】 A 10．已知圆的直径 AB＝13，C 为圆上一点，过 C 作 CD⊥AB 于 D(AD>BD)， 若 CD＝6，则 AD 的长为( ) A．8 B．9 C．10 D．11 【解析】 如图，连接 AC，CB. ∵AB 是⊙O 的直径， ∴∠ACB＝90°. 设 AD＝x，∵CD⊥AB 于 D， 由射影定理得 CD2＝AD·DB， 即 62＝x(13－x)，∴x2－13x＋36＝0， 解得 x1＝4，x2＝9. ∵AD>BD，∴AD＝9. 【答案】 B 11.某社区计划在一块上、下底边长分别是 10 米，20 米的梯形空地上种植花 木(如图 10 所示)，他们想在△AMD 和△BMC 地带种植单价为 10 元/米 2 的太阳 花，当△AMD 地带种满花后，已经花了 500 元，请你预算一下，若继续在△BMC 地带种植同样的太阳花，还需资金( ) 图 10 A．500 元 B．1 500 元 C．1 800 元 D．2 000 元 【解析】 在梯形 ABCD 中，AD∥BC，∴△AMD∽△BMC， AD＝10 m，BC＝20 m， S△AMD S△BMC ＝ 10 20 2＝1 4 ， ∵S△AMD＝500÷10＝50(m2)，∴S△BMC＝200 m2， 则还需要资金 200×10＝2 000(元)． 【答案】 D 12．如图 11 所示，将一个矩形纸片 BADC 沿 AD 和 BC 的中点连线 EF 对折， 要使矩形 AEFB 与原矩形相似，则原矩形的长与宽的比应为( ) 图 11 A．1∶ 2 B．1∶ 3 C. 2∶1 D. 3∶1 【解析】 ∵矩形 AEFB∽矩形 ABCD，∴BF∶AB＝AB∶AD. ∵BF＝1 2AD，∴AB2＝1 2AD2，∴AD∶AB＝ 2∶1. 【答案】 C 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分，请把答案填在题中横 线上) 13．如图 12，已知 DE∥BC，且 BF∶EF＝4∶3，则 AC∶AE＝________. 图 12 【解析】 ∵DE∥BC， ∴BC DE ＝BF EF ， 同理AC AE ＝BC DE ， ∴AC AE ＝BC DE ＝BF EF ＝4 3. 【答案】 4∶3 14．如图 13，王华晚上由路灯 A 下的 B 处走到 C 处时，测得影子 CD 的长 为 1 米，继续往前走 3 米到达 E 处时，测得影子 EF 的长为 2 米，已知王华的身 高是 1.5 米，那么路灯 A 的高度 AB 等于________米. 【导学号：07370026】 图 13 【解析】 如图，GC⊥BC，AB⊥BC，∴GC∥AB. ∴△GCD∽△ABD，∴DC DB ＝GC AB. 设 BC＝x，则 1 x＋1 ＝1.5 AB ，同理，得 2 x＋5 ＝1.5 AB. ∴ 1 x＋1 ＝ 2 x＋5 ，∴x＝3，∴ 1 3＋1 ＝1.5 AB ， ∴AB＝6(米)． 【答案】 6 15．如图 14 所示，在△ABC 中，AD 是 BC 边上的中线，BE 是 AC 边上的 中线，且 AD，BE 交于点 G，那么S△BDG S△ABC ＝________. 图 14 【解析】 ∵AD，BE 是△ABC 的中线，且 AD 交 BE 于 G， ∴G 是△ABC 的重心，∴DG AD ＝1 3 ， ∴S△BDG S△ABD ＝1 3 ， 又∵D 为 BC 的中点，∴S△ABD S△ABC ＝1 2 ，∴S△BDG S△ABC ＝1 6. 【答案】 1 6 16．如图 15，在矩形 ABCD 中，AB＝ 3，BC＝3，BE⊥AC，垂足为 E，则 DE＝________. 图 15 【解析】 法一：因为 AB＝ 3，BC＝3，所以 AC＝ 32＋ 32＝2 3，tan ∠ BAC＝ 3 3 ＝ 3，所以∠BAC＝π 3.在 Rt△BAE 中，AE＝ABcos π 3 ＝ 3 2 ，则 CE＝2 3 － 3 2 ＝3 3 2 .在△ECD 中，DE2＝CE2＋CD2－2CE·CDcos ∠ECD＝ 3 3 2 2＋( 3)2 －2×3 3 2 × 3×1 2 ＝21 4 ，故 DE＝ 21 2 . 法二：如图，作 EM⊥AB 交 AB 于点 M，作 EN⊥AD 交 AD 于点 N.因为 AB ＝ 3，BC＝3，所以 tan ∠BAC＝ 3 3 ＝ 3，则∠BAC＝π 3 ，AE＝ABcos π 3 ＝ 3 2 ， NE＝AM＝AEcosπ 3 ＝ 3 2 ×1 2 ＝ 3 4 ，AN＝ME＝AEsin π 3 ＝ 3 2 × 3 2 ＝3 4 ，ND＝3－3 4 ＝ 9 4.在 Rt△DNE 中，DE＝ NE2＋ND2＝ 3 4 2＋ 9 4 2＝ 21 2 . 【答案】 21 2 三、解答题(本大题共 6 小题，共 70 分．解答时应写出文字说明、证明过程 或演算步骤) 17．(本小题满分 10 分)如图 16，点 E 是四边形 ABCD 的对角线上一点，且 ∠BAC＝∠BDC＝∠DAE. 图 16 (1)求证：BE·AD＝CD·AE； (2)根据图形的特点，猜想BC DE 可能等于哪两条线段的比(只写出图中一组比即 可)？并证明你的猜想． 【解】 (1)证明：∵∠BAC＝∠DAE， ∴∠BAE＝∠DAC. ∵∠DAE＝∠BDC，∴∠AEB＝∠ADC， ∴△ABE∽△ACD，∴BE CD ＝AE AD ， 即 BE·AD＝CD·AE. (2)猜想：BC DE ＝AB AE AC AD . 证明：∵由(1)△ABE∽△ACD，∴AB AC ＝AE AD ， 又∵∠BAC＝∠EAD，∴△BAC∽△EAD， ∴BC DE ＝AB AE AC AD . 18．(本小题满分 12 分)如图 17，已知正方形 ABCD 的边长为 4，P 为 AB 上 的一点，且 AP∶PB＝1∶3，PQ⊥PC，试求 PQ 的长． 图 17 【解】 ∵PQ⊥PC， ∴∠APQ＋∠BPC＝90°， ∴∠APQ＝∠BCP， ∴Rt△APQ∽Rt△BCP. ∵AB＝4，AP∶PB＝1∶3， ∴PB＝3，AP＝1，∴AP BC ＝AQ BP ， 即 AQ＝AP·BP BC ＝1×3 4 ＝3 4 ， ∴PQ＝ AQ2＋AP2＝ 9 16 ＋1＝5 4. 19．(本小题满分 12 分)在△ABC 中，∠B＝25°，AD 是 BC 边上的高，并且 AD2＝BD·DC，求∠BCA 的度数． 【解】 (1)当 AD 在△ABC 内部时，如图(1)，由 AD2＝BD·DC，可得△ABD ∽△CAD. ∴∠BCA＝∠BAD＝65°； (2)当 AD 在△ABC 外部时，如图(2)， 由 AD2＝BD·DC，得△ABD∽△CAD， ∴∠B＝∠CAD＝25°， ∴∠BCA＝∠CAD＋∠ADC＝25°＋90°＝115°. 故∠BCA 等于 65°或 115°. 20．(本小题满分 12 分)如图 18 所示，CD 为 Rt△ABC 斜边 AB 边上的中线， CE⊥CD，CE＝10 3 ，连接 DE 交 BC 于点 F，AC＝4，BC＝3.求证： 图 18 (1)△ABC∽△EDC； (2)DF＝EF. 【证明】 (1)在 Rt△ABC 中，AC＝4，BC＝3，则 AB＝5. ∵D 为斜边 AB 的中点， ∴AD＝BD＝CD＝1 2AB＝2.5， ∴CD CE ＝2.5 10 3 ＝3 4 ＝BC AC ，∴△ABC∽△EDC. (2)由(1)知，∠B＝∠CDF， ∵BD＝CD，∴∠B＝∠DCF， ∴∠CDF＝∠DCF. ∴DF＝CF.① 由(1)知，∠A＝∠CEF，∠ACD＋∠DCF＝90°，∠ECF＋∠DCF＝90°， ∴∠ACD＝∠ECF.由 AD＝CD，得∠A＝∠ACD. ∴∠ECF＝∠CEF， ∴CF＝EF.② 由①②，知 DF＝EF. 21．(本小题满分 12 分)已知在等腰梯形 ABCD 中，AD∥BC，直线 MN 是梯 形的对称轴，P 是 MN 上的一点，直线 BP 交直线 DC 于 F，交 CE 于 E，且 CE ∥AB. (1)若点 P 在梯形内部，如图 19(1)． 求证：BP2＝PE·PF. (2)若点 P 在梯形的外部，如图 19(2)，那么(1)的结论是否成立？若成立，请 证明；若不成立，请说明理由． (1) (2) 图 19 【解】 (1)证明：连接 PC，因为 MN 是梯形 ABCD 的 对称轴，所以 PB＝PC， ∠PBC＝∠PCB. 因为梯形 ABCD 是等腰梯形， 所以∠ABC＝∠DCB， 即∠ABP＋∠PBC＝∠PCB＋∠DCP， 所以∠ABP＝∠DCP. 又因为 CE∥AB，所以∠E＝∠ABP＝∠DCP， 而∠CPE＝∠FPC，所以△CPE∽△FPC. 所以PE PC ＝PC PF ，即 PC2＝PE·PF， 又因为 PC＝BP，所以 BP2＝PE·PF. (2)结论成立．证明如下： 连接 PC， 由对称性知 PB＝PC， 所以∠PBC＝∠PCB. 因为梯形 ABCD 是等腰梯形， 所以∠ABC＝∠DCB， 所以∠ABC＋∠PBC＝∠DCB＋∠PCB， 即∠ABP＝∠DCP. 因为 CE∥AB，所以∠ABP＋∠PEC＝180°，而∠DCP＋∠PCF＝180°， 所以∠PEC＝∠PCF.又因为∠EPC＝∠CPF，所以△EPC∽△CPF. 所以PE PC ＝PC PF ，即 PC2＝PE·PF， 所以 BP2＝PE·PF. 22．(本小题满分 12 分)如图 20，在△ABC 中，AC＝BC，F 为底边 AB 上的 一点，BF AF ＝m n(m，n>0)．取 CF 的中点 D，连接 AD 并延长交 BC 于 E. 图 20 (1)求BE EC 的值； (2)如果 BE＝2EC，那么 CF 所在的直线与边 AB 有怎样的位置关系？证明你 的结论； (3)E 点能否为 BC 中点？如果能，求出相应的m n 的值；如果不能，证明你的 结论． 【导学号：07370027】 【解】 (1)如图所示，作 CG∥AB 交 AE 的延长线 于 G. 在△GCD 与△AFD 中， ∠G＝∠FAD，∠CDG＝∠FDA，DC＝DF， ∴△GCD≌△AFD，∴GC＝AF. 在△ABE 和△GCE 中， ∠BAE＝∠G，∠AEB＝∠GEC， ∴△ABE∽△GCE.∵BF AF ＝m n(m，n>0)， ∴BE EC ＝AB GC ＝BF＋AF AF ＝BF AF ＋1＝m n ＋1. (2)∵BE＝2EC，∴BE EC ＝2. 由(1)知BE EC ＝m n ＋1，∴m n ＝1. ∴BF＝AF，F 为 AB 的中点． ∵AC＝BC，∴CF⊥AB，∴CF 所在的直线垂直平分边 AB. (3)不能．∵BE EC ＝m n ＋1，而m n>0，∴BE EC>1， ∴BE>EC. ∴E 不能为 BC 的中点．