湖北省襄阳五中、夷陵中学、钟祥一中三校2020届高三下学期6月高考适应性考试文科数学试题 Word版含解析 26页

- 1 - 2020 届襄阳五中、夷陵中学、钟祥一中三校 高三 6 月适应性考试文科数学试题 注意事项： 1.答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在 答题卡上的指定位置. 2.选择题的作答：每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑.写在 试卷、草稿纸和答题卡上的非答题区域均无效. 3.非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和 答题卡上的非答题区域均无效. 4.选考题的作答：先把所选题目的题号在答题卡上指定的位置用 2B 铅笔涂黑.答案写在答题 卡上对应的答题区域内，写在试卷、草稿纸和答题卡上的非答题区域均无效. 5.考试结束后，请将本试卷和答题卡一并上交. 一、选择题：本题共 12 小题，每小题 5 分，共 60 分，在每小题给的四个选项中，只有一项 是符合题目要求的. 1. 已知集合 2{ | 4 }A x y x   ，集合 { | }B x x a  ，若 A B ，则实数 a 的取值范围是 （ ） A.  , 2  B.  , 2  C.  2  ， D.  2 ， 【答案】B 【解析】 【分析】 由题意得，  2,2A   ，再根据集合间包含关系即可求出答案． 【详解】解：∵  2{ | 4 } 2,2A x y x     ， { | }B x x a  ， A B ， ∴ 2a   ， 故选：B． 【点睛】本题主要考查根据集合间的包含关系求参数的取值范围，考查一元二次不等式的解 法，属于基础题． 2. 已知i 为虚数单位，若复数 (1 2 ) 3i z i   ，则| |z  （ ） - 2 - A. 5 2 3 B. 26 5 C. 2 D. 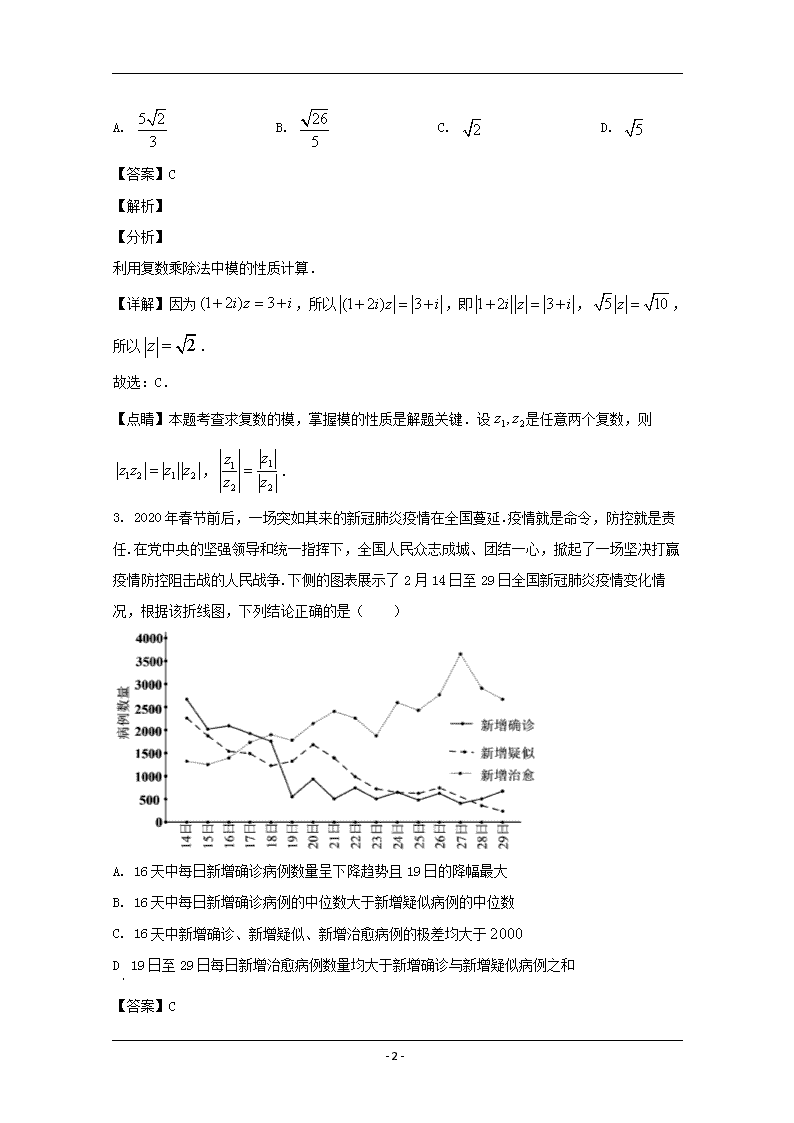5 【答案】C 【解析】 【分析】 利用复数乘除法中模的性质计算． 【详解】因为 (1 2 ) 3i z i   ，所以 (1 2 ) 3i z i   ，即 1 2 3i z i   ， 5 10z  ， 所以 2z  ． 故选：C． 【点睛】本题考查求复数的模，掌握模的性质是解题关键．设 1 2,z z 是任意两个复数，则 1 2 1 2z z z z ， 11 2 2 zz z z  ． 3. 2020 年春节前后，一场突如其来的新冠肺炎疫情在全国蔓延.疫情就是命令，防控就是责 任.在党中央的坚强领导和统一指挥下，全国人民众志成城、团结一心，掀起了一场坚决打赢 疫情防控阻击战的人民战争.下侧的图表展示了 2 月 14 日至 29 日全国新冠肺炎疫情变化情况， 根据该折线图，下列结论正确的是（ ） A. 16 天中每日新增确诊病例数量呈下降趋势且 19 日的降幅最大 B. 16 天中每日新增确诊病例的中位数大于新增疑似病例的中位数 C. 16 天中新增确诊、新增疑似、新增治愈病例的极差均大于 2000 D. 19 日至 29 日每日新增治愈病例数量均大于新增确诊与新增疑似病例之和 【答案】C - 3 - 【解析】 【分析】 由折线图分别观察变化趋势，估计中位数，计算极差，确认新增治愈病例数量与新增确诊与 新增疑似病例之和，判断各选项后可得结论． 【详解】从新增确诊折线看 19 日降幅最大，但并不呈下降趋势，如 20 日比 19 日就是上升的， 27,28,29 三天还是增加的趋势，A 错； 新增确诊病例和新增疑似病例的中位数在 21、22 日前后，新增疑似病例的中位数比新增确诊 病例的中位数大，B 错； 三根折线中最大值与最小值的差都大于 2000，C 正确； 20 日新增治愈病例数量小于新增确诊与新增疑似病例之和，D 错误． 故选：C． 【点睛】本题考查折线图的认识，考查学生的数据处理能力．属于基础题． 4. 将一个各面上均涂有颜色的正方体的棱四等分，然后沿等分线把正方体切开得到同样大小 的小正方体，从这些小正方体中任取一个，则恰好没有被涂色的概率为（ ） A. 1 8 B. 1 4 C. 3 8 D. 1 2 【答案】A 【解析】 【分析】 根据古典概型的概率公式计算可得结果. 【详解】沿等分线把正方体切开得到同样大小的小正方体共有 64 个，其中有 3 个面涂色的小 正方体共有 8 个，只有 2 个面涂色的小正方体共有12 2 24  个，只有一个面涂色的小正方 体共有 2446  个，那么没有被涂色的小正方体共有 64 8 24 24 8    个， 所以恰好没有被涂色的概率为 8 1 64 8  . 故选：A. 【点睛】本题考查了古典概型的概率公式，属于基础题. - 4 - 5. 已知   1 2 |1 2 |x xf x     ，则  f x 的值域是（ ） A.  ,2 B.  0,2 C.  0 3, D.  1,2 【答案】B 【解析】 【分析】 根据指数函数的性质分类讨论去掉绝对值求出各段区间上的值域，再求函数  f x 的值域． 【详解】解：当1 2 0x  ，即 0x  时，     11 2 1 2 2x x xf x      ，则  0 2f x  ， 当1 2 0x  ，即 0x  时，    1 2 1 2 2x xf x      ， ∴  f x 的值域是 0,2 ， 故选：B． 【点睛】本题主要考查分段函数的值域，考查指数函数的性质，属于基础题． 6. 在平面直角坐标系 xOy 中，已知任意角 以 x 轴的正半轴为始边，若终边经过点 P 0 0( , )x y 且 ( 0)OP r r  ，定义： 0 0cos y xsi r   ，称“ cossi  ”为“正余弦函数”；对于正余 弦函数 cosy si x ，以下性质中正确的是（ ） A. 函数关于 2x  对称 B. 函数关于 ( ,0)2  对称 C. 函数在 3[0, ]4  单调递增 D. 函数值域为[ 2,2] 【答案】C 【解析】 【分析】 首先根据题意，求出 cos 2 sin( )4y si x x    ，然后根据正弦函数的图象和性质逐一判断即 可． 【详解】解：根据三角函数的定义可知 0 cosx r x ， 0 siny r x ， 所以 0 0 sin coscos sin cos 2 sin( )4 y x r x r xy si x x x xr r         ， 即   cos 2 sin( )4y f x si x x     - 5 - 因为 1 sin( ) 14x  „ „ ， 所以 2 2 sin( ) 24x  „ „ ， 即该函数的值域为 2, 2   ； 因为   cos 2 sin( )4f x si x x    所以 cos 2 sin 12 2 2 4f si                ，故函数不关于 2x  对称且不关于 ,02      对称， 令 2 22 4 2k x k         ，  k Z 解得 32 24 4k x k       ，  k Z ， 即函数的单调递增区间为 32 , 24 4k k        ，  k Z ，故 C 正确； 故选：C 【点睛】本题主要考查了三角函数的图象和性质，属于中档题，解答此题的关键是首先求出 函数 cosy si  的表达式． 7. 若正整数 N 除以正整数 m 后的余数为 n ，则记为 (mod )N n m ，例如10 4(mod6) ．右 边程序框图的算法源于我国古代闻名中外的《中国剩余定理》．执行该程序框图，则输出的 n 等 于（ ） - 6 - A. 17 B. 16 C. 15 D. 13 【答案】A 【解析】 根据算法的程序框图知，从 n=11 开始，依次增加 1，对应的正整数要同时满足 n=2（mod3）， 及 n=2（mod5）时，即被 3 除余 2，被 5 除余 2，才结束循环，输出 n 的值，满足条件的 n=17. 故选 A. 8. 已知 0 1y x   ， 1x y  ， log 2xy x ya  ， cosb y ， 1( )yc x  的，则 , ,a b c 的大 小关系是（ ） A. c b a  B. c a b  C. a b c  D. b c a  【答案】A 【解析】 【分析】 对 a 可根据不等式以对数函数的单调性，得到 a 的大致范围，对b 根据余弦函数的单调性得到 大致范围，对 c 根据指数函数的单调性确定大致范围，从而比较出 , ,a b c 的大小. - 7 - 【详解】由 0 1y x   ， 1x y  ，则 2 1 2 4 x yxy      ， 1 2logxya   1 2 1 log ( )xy ， 由 1 1 2 2 1log ( ) log 24xy   ，故 10 2a  ； 由 0 1 3y    ，则 cos0 cos cos1y  cos 3  ，得 11 cos 2y  ，即 1 12 b  ； 由 0 1y x   ，则 1 1x  ， 0y  ，得 01 1( ) ( )yc x x   ，得 1c  ； 故 c b a  . 故选：A 【点睛】本题考查了比较数的大小，根据函数的单调性，得到大致范围，从而比较出数的大 小. 9. 数列的发展史，折射出许多有价值的数学思想方法，对时代的进步起了重要作用，比如意 大利数学家列昂纳多·斐波拉契以兔子繁殖为例，引入“兔子数列”：即 1,1,2,3,5,8,13,21,34,55,89,144,233···也即 (1) (2) 1F F  ， ( ) ( 1) ( 2)F n F n F n    ( 3, )n n N   ，若此数列被 4 整除后的余数构成一个新的数列 nb ，则 1 2 3 2020b b b b     （ ） A. 2695 B. 3535 C. 2023 D. 2020 【答案】A 【解析】 【分析】 由题意可得： 1 1b  ， 2 1b  ， 3 2b  ， 4 3b  ， 5 1b  ， 6 0b  ； 7 1b  ， 8 1b  ， 9 2b ， 10 3b  ， 11 1b  ， 12 0b  ，．可得数列{ }nb 是周期为 6 的数列，从而求出数列的前 2020 项和； 【详解】解：由题意可得： 1 1b  ， 2 1b  ， 3 2b  ， 4 3b  ， 5 1b  ， 6 0b  ； 7 1b  ， 8 1b  ， 9 2b ， 10 3b  ， 11 1b  ， 12 0b  ，． 数列{ }nb 是周期为 6 的数列， - 8 - 所以  1 2 3 2020 1 2 3 4 5 6 1 2 3 4336b b b b b b b b b b b b b b                1 1 2 3 1 0 336 1 1 2 3 2695            故选：A 【点睛】本题考查了数列递推关系、斐波那契数列的性质、数列的周期性，考查了推理能力 与计算能力，属于中档题． 10. 已知双曲线 2 2: 14 xC y  ， 1 2,F F 分别为双曲线的左右焦点， 0 0( , )P x y 为双曲线C 上 一点，且位于第一象限，若三角形 1 2PF F 为锐角三角形，则 0y 的取值范围为（ ） A. 5( , )5  B. 2 5( , )5  C. 5 1( , )5 2 D. 1 2 5( , )2 5 【答案】C 【解析】 【分析】 因为 P 位于第一象限，所以 1 2PF F 恒为锐角，由 2 1PF F 为锐角可得 02 5x  ， 0 1(0, )2y  ，由 1 2F PF 为锐角得 1 2 0PF PF   ，利用平面向量积可得答案. 【详解】由 2 2 14 x y  得 1( 5,0)F  、 2 ( 5,0)F ， 因为 P 位于第一象限，所以 1 2PF F 恒为锐角， 因为三角形 1 2PF F 为锐角三角形，所以 2 1PF F 为锐角， 1 2F PF 为锐角， 由 2 1PF F 为锐角得 02 5x  ，所以 2 2 0 0 11 (0, )4 4 xy    ，因为 0 0y  ，所以 0 1(0, )2y  ， 由 1 2F PF 为锐角得 1 2 0PF PF   ， 所以 0 0 0 0( 5 , ) ( 5 , ) 0x y x y       ， 所以 2 0 0 0( 5 )( 5 ) 0x x y     ， - 9 - 所以 2 2 0 0 5 0x y   ， 又 2 20 0 14 x y  ，所以 2 2 0 04 4 5 0y y    ，即 2 0 1 5y  ，又 0 0y  ，所以 0 5 5y  ， 综上所述： 0 5 1( , )5 2y  . 故选：C. 【点睛】本题考查了双曲线的几何性质，考查了平面向量数量积，考查了运算求解能力，考 查了锐角三角形的概念，属于基础题. 11. 平面四边形 ABCD 为凸四边形，且 60A   ，AD DC ， 3AB  ， 2BD  ，则 BC 的取值范围为（ ） A. 7[ ,2)2 B. 7( ,2)2 C.  2 7， D. 7[ , 7)2 【答案】D 【解析】 【分析】 由余弦定理求出 AD ，作出直角三角形 ADE（ E 是 ,DC AB 的交点），点C 在线段 ED（不 含端点）上，求出 7BE  ，再求出 B 到直线 DE 的距离即可得出结论． 【 详 解 】 设 AD x ， 在 ABD△ 中 ， 2 2 2 2 cosBD AB AD AB AD A    ， 所 以 24 3 2 3 cos60x x    ，解得 3 7 2x  ， 延长 ,DC AB 交于点 E ，则由 AD CD 得 3 7AE   ， 7BE  ， 若 BC CD ，则 7 2BC  ， 显然点C 在线段 ED （不含端点）上，所以 BC 的取值范围是 7[ , 7)2 ． 故选：D． - 10 - 【点睛】本题考查解三角形的应用，掌握余弦定理是解题关键． 12. 如图，在棱长为 2 的正方体 1 1 1 1ABCD A B C D 中， , ,E F G 分别是棱 1, ,AB BC CC 的中 点， P 是底面 ABCD 内一动点，若直线 1D P 与平面 EFG 不存在公共点，以下说法正确的个 数是（ ） ①三棱锥 P EFG 的体积为定值； ② 1PBB 的面积的最小值为 2 ； ③ 1B D  平面 EFG ； ④经过 , ,E F G 三点的截面把正方体分成体积相等的两部分. A. 1 B. 2 C. 3 D. 4 【答案】D 【解析】 【分析】 由题意得， 1 //D P 平面 EFG ，连接 1 1 1, , ,AD AC CD BC ，则 1 1//AD BC ，可得 //AC 平面 EFG ， 1 //AD 平面 EFG ，由此得平面 1 //ACD 平面 EFG ，则点 P 在直线 AC 上，从而有 PEF 的 面积 PEFS△ 为定值，由此可判断①；结合题意得，当点 P 为 ,AC BD 的交点时， AC PB ， PB 有最小值 1 22PB BD  ，由此可判断②；由题意可得 AC  平面 1 1BB D D ，从而推出 - 11 - 1EF B D ， 1GF B D ，由此可判断③；将平面 EFG 补成平面 EFGHIJ （ , ,H I J 均为各 条棱的中点），结合图象可判断④． 【详解】解：∵直线 1D P 与平面 EFG 不存在公共点， ∴ 1 //D P 平面 EFG ， 连接 1 1 1, , ,AD AC CD BC ，则 1 1//AD BC ， ∵ , ,E F G 分别是棱 1, ,AB BC CC 的中点， ∴ //EF AC ， 1 1/// /GF BC AD ， ∵ AC  平面 EFG ， EF  平面 EFG ， ∴ //AC 平面 EFG ， 同理， 1 //AD 平面 EFG ， 又 1AC AD AI ， ∴平面 1 //ACD 平面 EFG ， ∵ 1 //D P 平面 EFG ，平面 1ACD 平面 ABCD AC ， 1D P 平面 1ACD ， ∴点 P 在直线 AC 上， ∵ //EF AC ， ∴ PEF 的面积 PEFS△ 为定值， ∴三棱锥 P EFG 的体积 P EFG G PEFV V  为定值，则①对； ∵ //EF AC ， ∴当点 P 为 ,AC BD 的交点时， AC PB ， PB 有最小值 1 22PB BD  ， - 12 - 此时，直角 1PBB 的面积有最小值，且 1 1 1 2PBBS PB BB   1 2 2 22     ，则②对； ∵在正方体 1 1 1 1ABCD A B C D 中， AC BD ， 由 1BB  平面 ABCD 得， 1AC BB ， ∴ AC  平面 1 1BB D D ，∴ 1AC B D ，则 1EF B D ， 同理， 1GF B D ， ∴ 1B D  平面 EFG ，则③对； 将平面 EFG 补成平面 EFGHIJ （ , ,H I J 均为各条棱的中点），如图， 则平面 EFG 将正方体分成两个大小形状完全相同的部分（均由一个正六棱锥和三个三棱锥拼 接而成），则④对； 故选：D． 【点睛】本题主要考查空间中的点、线、面的位置关系，考查几何体的体积的求法，属于中 档题． 二、填空题：本题共 4 小题，每小题 5 分，共 20 分. 13. 已知抛物线  2 2 0y px p  的焦点是双曲线 2 2 18 x y p   的一个焦点，则双曲线的渐近 线方程为___________. 【答案】 y x  【解析】 【分析】 根据题意可得出关于 p 的方程，解出正数 p 的值，可得出双曲线的标准方程，进而可得出双 曲线的渐近线方程. 【详解】抛物线  2 2 0y px p  的焦点坐标为 ,02 p     ， 由题意可知，点 ,02 p     为双曲线 2 2 18 x y p   的一个焦点，则 8 2 pp  ，整理得 2 4 32 0p p   ， - 13 - 0p  ，解得 8p  ，所以，双曲线的标准方程为 2 2 18 8 x y  . 因此，双曲线的渐近线方程为 y x  . 故答案为： y x  . 【点睛】本题考查双曲线渐近线方程的求解，同时也考查了利用抛物线与双曲线的焦点求参 数，考查计算能力，属于基础题. 14. 已知圆 2 22 2 2 1 0x x y my m      ，当圆的面积最小时，直线 y x b  与圆相切， 则b  __________. 【答案】 2 【解析】 【分析】 利用圆的面积最小得圆的半径最小，可得 1m  ，再根据圆心到直线的距离等于半径可得答案. 【 详 解 】 将 2 22 2 2 1 0x x y my m      化 为 标 准 方 程 为 2 2 2( 1) ( ) 2 2x y m m m      ， 所以圆的半径为 2 2 2m m  ， 当圆面积最小时，圆的半径最小，此时 1m  ，圆的方程为 2 2( 1) ( 1) 1x y    ， 因为直线 y x b  与圆相切，所以 |1 1 | 1 2 b   ，解得 2b   . 故答案为： 2 . 【点睛】本题考查了由圆的标准方程求圆心坐标和半径，考查了直线与圆相切的位置关系， 考查了点到直线的距离，属于基础题. 15. 已知正方形 ABCD 的边长为 2 ，平面 ABCD 内的动点 P 满足 1CP  ，则 PD PA  的最 大值是______. 【答案】5 2 5 【解析】 【分析】 - 14 - 建立平面直角坐标系，设  ,P x y ，根据 1CP  ，得到 ,x y 的方程，再利用三角换元，通过 三角恒等变换得到 PD PA   5 2 5 sin ,tan 2      ，然后利用正弦函数的性质求解. 【详解】建立如图所示平面直角坐标系： 因为正方形 ABCD 的边长为 2 ， 所以      0,0 , 2,2 , 0,2A C D ， 设  ,P x y ，则      2, 2 , ,2 , ,CP x y PD x y PA x y           ， 因为 1CP  ， 所以    2 22 2 1x y    ， 令 2 cos , 2 sinx y     ， 所以    ,2 , ,PD x y PA x y       ， 所以  22 1 1PD PA x y      ， 5 2sin 4cos    ，  5 2 5 sin ,tan 2      ， 所以 PD PA  的最大值是5 2 5 . 故答案为：5 2 5 - 15 - 【点睛】本题主要考查平面向量的模，数量积的坐标运算以及三角恒等变换，还考查了数形 结合的思想和运算求解的能力，属于中档题. 16. 对于任意实数 1 2,x x ，当 1 20 x x e   时，有 1 2 2 1 2 1ln lnx x x x ax ax   恒成立，则实 数 a 的取值范围为___________. 【答案】 0a  【解析】 【分析】 转化为 ln( ) x ag x x  在 (0, )e 上单调递增，再利用导数可得到结果. 【 详 解 】 当 1 20 x x e   时 ， 1 2 2 1 2 1ln lnx x x x ax ax   恒 成 立 等 价 于 2 1 2 1 ln lnx a x a x x   恒成立，等价于 ln( ) x ag x x  在 (0, )e 上单调递增， 所以 2 2 1 ln 1 ln( ) 0 x x a x axg x x x         在 (0, )e 上恒成立， 所以 1 lna x  在 (0, )e 上恒成立， 因为当 (0, )x e 时，1 ln 1 ln 0x e    ， 所以 0a  . 故答案为： 0a  . 【点睛】本题考查了转化划归思想，考查了利用导数研究函数的单调性，考查了利用导数处 理不等式恒成立问题，属于基础题. 三、解答题：共 70 分.解答应写出文字说明、证明过程或演算步骤.第 1721 题为必考题，每 个试题考生都必须作答.第 22、23 题为选考题，考生根据要求作答. （一）必考题： 17. 疫情过后，某商场开业一周累计生成 2 万张购物单，从中随机抽出 100 张，对每单消费 金额进行统计得到下表： 消费金额（单位：元） (0,200] (200,400] (400,600] (600,800] (800,1000] 购物单张数 25 25 30 ？ ？ - 16 - 由于工作人员失误，后两栏数据已无法辨识，但当时记录表明，根据由以上数据绘制成的频 率分布直方图所估计出的每单消费额的中位数与平均数恰好相等（用频率估计概率），完成下 列问题： （1）估计该商场开业一周累计生成的购物单中，单笔消费额超过 800 元的购物单张数； （2）为鼓励顾客消费，拉动内需，该商场打算在今年国庆期间进行促销活动，凡单笔消费超 过 600 元者，可抽奖一次，中一等奖、二等奖、三等奖的顾客可以分别获得价值300 元、100 元、 50 元的奖品.已知中奖率为 100%，且一等奖、二等奖、三等奖的中奖率依次构成等差数 列，其中一等奖的中奖率为 1 21 .若今年国庆期间该商场的购物单数量预计比疫情后开业一周 的购物单数量增长 5%，试预测商场今年国庆期间采办奖品的开销. 【答案】（1）1000（张）（2）采购奖品的开销可估计为 330000 （元） 【解析】 【分析】 （1）由中位数的定义，根据概率为 1 2 ，求得中位数，设消费在区间 (800,1000]内的概率为 p ， 根据中位数与平均数恰好相等解得 p 即可. （2）根据中奖率为 100%，且一等奖、二等奖、三等奖的中奖率依次构成等差数列，其中一等 奖的中奖率为 1 21 ，设等差数列的公差为 ( 0)d d  ，由 1 1 1( ) ( 2 ) 121 21 21d d     ，解得 d ， 得到一等奖、二等奖、三等奖的中奖率，再根据购物单数量增长 5%，得到今年的购物具有抽 奖资格的单数，从而得到一等奖、二等奖、三等奖中奖单数，即可得到采购奖品的开销. 【详解】（1） 25 25 1 100 2   ， 中位数为 400 ， 又 25 25 30 0.8100    设消费在区间 (800,1000]内的概率为 p ， 则消费在区间 (600,800]内的概率为 0.2 p 由中位数与平均数恰好相等可知， 100 0.25 300 0.25 500 0.3 700 (0.2 ) 900 400p p           ， - 17 - 解得 0.05p  ， 故单笔消费超过 800 元的购物单张数为： 20000 0.05 1000  （张）. （2）设等差数列的公差为 ( 0)d d  ， 则 1 1 1( ) ( 2 ) 121 21 21d d     ， 解得 2 7d  ， 故一等奖、二等奖、三等奖的中奖率分别为 1 1 13, ,21 3 21 今年的购物具有抽奖资格的单数约为 20000 1.05 0.2 4200   ， 故一等奖、二等奖、三等奖中奖单数可估计为 200,1400,2600 ， 采购奖品的开销可估计为 200 300 1400 100 2600 50 330000      （元）. 【点睛】本题主要考查频率分布表的应用，中位数，平均数的求法，还考查了运算求解的能 力，属于中档题. 18. 已知等比数列{ }na 前 n 项和为 nS ，且 1 1 32n nS a   ( )n N . （1）求数列{ }na 的通项公式； （2）若 2logn nb a ，求数列{| |}nb 的前 n 项和 nT . 【答案】（1） 62n na  （2） 2 2 11 , 62 11 30, 62 n n n n T n n n        【解析】 【分析】 （1）利用 1( 2)n n na S S n   可得数列{ }na 的递推关系，由 1n  可得 1 2,a a 的关系，由等 比数列可求得 1 2,a a ，从而得通项公式； （2）由（1）求出 nb ，{ }nb 前 5 项是负数，从第 6 项起各项非负，可对 n 分类讨论： 5n  或 6n  ，然后结合等差数列的前 n 项和公式得结论． 【详解】解：（1）当 1n  时， 1 2 2 1 1 1,32 32S a a a    ， - 18 - 当 2n  时， 1 1 32n nS a   ，与已知式作差得 1n n na a a  ，即 1 2 ( 2)n na a n   欲使{ }na 为等比数列，则 2 12a a ，又 2 1 1 32a a  ， 1 1 32a  故数列{ }na 是以 1 32 为首项， 2 为公比的等比数列，所以 62n na  （2） 6nb n  ， 6 , 6 6, 6n n nb n n      ， 若 6n  ， 2 1 11 2n n n nT b b      若 6n  ， 2 1 5 6 11 302n n n nT b b b b           ， 2 2 11 , 62 11 30, 62 n n n n T n n n         ． 【点睛】本题考查由 nS 与 na 的关系求通项公式，考查含绝对值的等差数列的求和，解题时在 利用 1n n na S S   时要注意 2n  ．含绝对值的问题，一般要根据绝对值定义去掉绝对值符号， 因此需要分类讨论． 19. 如图所示，四棱锥 P ABCD 的底面 ABCD 是直角梯形， / /BC AD ， AB AD ， 1 2AB BC AD  ，PA  底面 ABCD ，过 BC 的平面交 PD 于 M ，交 PA 于 N （ M 与 D 不重合）. （1）求证： / / BCMN ； （2）若 BM AC ，求 P BCMN P ABCD V V   的值. - 19 - 【答案】（1）证明见解析；（2） 1 3 【解析】 【分析】 （1）根据线面平行的性质定理即可证明 //MN BC ； （2）根据线面垂直的判定定理证明 BCDK 是平行四边形，即可证明 M 是 PD 的中点，最 后根据 2 2P BCMN P BCN C BPN C ABP P ABC ABC P ABCD P ABCD P ABCD P ABCD P ABCD ABCD V V V V V S V V V V V S                 梯形 即可得到结论． 【详解】证明：（1）在梯形 ABCD 中， //BC AD ， BC 平面 PAD ， AD 平面 PAD ，  //BC 平面 PAD . 又 BC 平面 BCNM ，平面 BCNM 平面 PAD = MN ， 所以 //MN BC . （2）过 M 作 //MK PA 交 AD 于 K ，连结 BK . 因为 PA  底面 ABCD ，所以 MK  底面 ABCD . 所以 MK AC .又因为 BM AC ， BM MK M ， 所以 AC  平面 BMK ，所以 AC BK . 所以在平面 ABCD 中可得 BCDK 是平行四边形. 所以 BC DK AK  ， 因为 K 是 AD 中点，所以 M 为 PD 中点. 设 1 2AB BC AD x   ， 则 22 2 1 3 3 P BCMN P BCN C BPN C ABP P ABC ABC P ABCD P ABCD P ABCD P ABCD P ABCD ABCD V V V V V S x V V V V V S x x                  梯形 - 20 - 【点睛】本题主要考查线面垂直和线面平行的判定和性质，综合考查空间直线和平面的位置 关系的判定，要求熟练掌握相应的判定定理和性质定理，考查学生的运算和推理能力，属于 中档题． 20. 抛物线 2 2 ( 0)x py p  的焦点为 F ，过焦点 F 的直线l 与抛物线交于 A B、 两点，点 A 到 x 轴的距离等于 1AF - . （1）求抛物线方程； （2）过 F 与 AB 垂直的直线和过 B 与 x 轴垂直的直线相交于点 M ， AM 与 y 轴交于点 N ， 求点 N 的纵坐标的取值范围. 【答案】（1） 2 4x y （2）   ,0 2,  【解析】 【分析】 （1）根据抛物线的定义求出 p 即可得到抛物线方程； （2）设 2 2 1 2 1 2( , ), ( , )4 4 x xA x B x ，直线 l 的方程为： 1y kx  ，联立直线 l 与抛物线，根据韦达 定理得 1 2 1 24 , 4x x k x x     ，由直线 l 与直线 MF 的方程得 2 2 1( , 1M x xk   ），设 (0, )N n ， 由 M N A、 、 三点共线，求得 2 1 2 1 2 4 xn x   ，进一步可得 n 的取值范围. 【详解】（1）由抛物线定义可知 12 p  ，即 2p  ， 所以抛物线的方程为 2 4x y . （2）设 2 2 1 2 1 2( , ), ( , )4 4 x xA x B x ，直线l 的方程为： 1y kx  ， - 21 - 由 2 4 1 x y y kx      消去 y 并整理得 2 4 4 0x kx   ， 所以 1 2 1 24 , 4x x k x x     ， 所以 1 2 4 x xk  . 由已知得直线 MF 的方程是； 1 1y xk    ， 2 2 1( , 1M x xk    ）. 设 (0, )N n ，由 M N A、 、 三点共线，可知 22 11 2 1 2 1 11 44 xx xn k x x x     ， 所以 22 11 2 1 2 1 2 1 41 44 xx xn x x x x x      ， 所以 2 3 1 1 2 1 2 1 1 1 2 4( )( )4 4 x x x xn x x x x x      所以 2 3 3 1 2 1 1 2 1 1 1 2 16( )4 4 4 x x x xn x x x x x       ， 所以 1 2 1 1 1 2 16( )x n x x x x x       ， 所以 1 1 1 1 1 4 16( ) 2 4n x xx x x     ， 所以 2 1 2 1 2 4 xn x   2 1 82 4x    ，所以 2 1 84 42x n     1( 0)x  ， 所以 2 0n   或 2 0 2 2 n n      ， 解得 2n  或 0n  . 【点睛】本题考查了根据抛物线的定义求抛物线方程，考查了直线与抛物线的位置关系，考 查了斜率公式的应用，考查了求直线与直线的交点坐标，考查了运算求解能力，属于中档题. - 22 - 21. 设 ( 2, 1)a   ，已知函数 3 2 2 1 1 ( 2) 2 03 2( ) 02 x a x ax x f x a x x         （1）讨论函数 ( )f x 的单调性； （2）设函数 ( )f x 在点 ( , ( ))( 1,2,3)i i iQ x f x i  处的切线互相平行，证明： 1 2 3 2x x x   . 【答案】（1） ( )f x 在 ( , 2)  上单调递增，在 ( 2, )  上单调递减（2）证明见解析； 【解析】 【分析】 （1）分段求出导函数，分类研究单调性，注意函数的连续性，有些单调区间可以连接起来． （2）易知 ( 1,2,3)iQ i  是直线 y m 与函数 ( )y f x 图象的三个交点，结合图象可得 1 2 3, ,x x x 的关系，从而可得证结论． 【详解】解：（1）当 0x  时， 2( ) ( 2) 2 ( 2)( )f x x a x a x x a       令 ( ) 0f x  ，则 2x   ， 当 ( , 2)x   时， ( ) 0f x  ， ( )f x 单调递增；当 ( 2,0)x   时， ( ) 0f x  ， ( )f x 单调递 减； 当 0x  时， ( ) 0f x ax  ，所以 ( )f x 在 (0, ) 上单调递减 又因为 ( )f x 在 R 上连续，故 ( )f x 在 ( , 2)  上单调递增，在 ( 2, )  上单调递减. （2）由图可知，直线 y m 与函数 ( )y f x 的图象有三个交点，横坐标为 1 2 3, ,x x x ， 不妨 1 2 30x x x   ，则 1 2 ( 2)x x a    又 3 2( )2 af ax   ，所以 2 3 ( 2)2 4 ax a   则 2 1 2 3 ( 2)( 2) 2 4 ax x x a a        ，化简得 1 2 3 5 1 14x x x a a       令t a  ， 5 1( ) 14g t t t    ， 2 5 1( ) 4g t t    ，因为 ( 2, 1)a   ，则 (1,2)t  ，所以 ( ) 0g t  ， ( )g t 在(1,2) 上单调递增， ( ) (2) 2g t g  ，即 1 2 3 2x x x   ． - 23 - 【点睛】本题考查用导数研究函数的单调性，考查导数的几何意义，注意分段函数需要分段 讨论．本题考查了学生的分析问题解决问题的能力，转化与化归能力，运算求解能力． （二）选考题：共 10 分.请考生在第 22、23 题中任选一题作答，如果多做，则按所做的第一 题计分 选修 4-4：坐标系与参数方程 22. 在直角坐标系 xoy 中，曲线 1C 的参数方程为 sin cos sin 2 x y        （ 为参数），若以该直 角坐标系的原点为极点， x 轴的正半轴为极轴，建立极坐标系，曲线 2C 的极坐标方程为 2 sin( )4 t    （其中t 为常数）. （1）求曲线 1C 和 2C 的直角坐标方程； （2）若曲线 1C 和 2C 有且仅有一个公共点，求t 的取值范围. 【答案】（1） 2 1x y  ； 0x y t   （2） 5(1 2,1 2] 4t         【解析】 【分析】 （1）根据三角恒等变换，把函数关系式变形，再通过消元求出函数的普通方程，根据 sin y   ， cos x   可将极坐标方程转化为直角坐标方程； （2）联立方程进行化简得到 2 1t x x   ，作出   2 1, [ 2, 2]    g x x x x 的图象， 数形结合分析出 y t 与二次函数有一个交点时，t 的取值范围. 【详解】（1）由 2 (sin cos ) 1 sin 2     ，可知曲线 1C 的直角坐标方程为 2 1x y  ， - 24 - 其中 sin cos 2 sin( ) [ 2, 2]4x         ，所以曲线 1C 的直角坐标方程为 2 1y x  ， [ 2, 2]x  ， 由 2 sin( )4 t    ，可得 sin cos t     ，由 sin y   ， cos x   ， 曲线 2C 的直角坐标方程为 0x y t   ； （2）由 2 1, [ 2, 2]{ 0        y x x x y t ，可知 2 1t x x   ， 令   2 1, [ 2, 2]    g x x x x ，其图象如下： 由曲线 1C 和 2C 有且仅有一个公共点，所以函数 y t 与   2 1, [ 2, 2]    g x x x x 的图 象有且仅有一个公共点，所以由图象可知 5(1 2,1 2] 4t         . 【点睛】本题主要考查参数方程、极坐标方程与普通方程的互化，以及用数形结合思想求参 数范围. 选修 4-5：不等式选讲 23. 已知函数 3( ) | 1| | |4f x x x m     的定义域为 R . （1）求实数 m 取值范围； （2）若实数 m 的最大值为 n ， 2 2 22 3a b c n   ，求证： 72 8ac bc  . 【答案】（1） 7 4m  （2）证明见解析； - 25 - 【解析】 【分析】 （1）依题意可得 031| | |4x x m    恒成立，参变分离可得 31 4m x x    ，再根据 绝对值三角不等式计算可得； （2）由（1）知 n  7 4 ，即 2 2 2 72 3 4a b c   ，再根据基本不等式即可证明； 【详解】解：（1） 3| 1| | 0| 4x x m     恒成立  31 4m x x    ，又 3 3 71 14 4 4x x x x        7 4m  （2）由（1）知 n  7 4 ，所以 2 2 2 72 3 4a b c   ， 又  2 2 2 2 2 2 22 3 2 2 4a b c a c b c ac bc        ， 所以 72 8ac bc  . 当且仅当 a b c  时取等号； 【点睛】本题考查绝对值三角不等式的应用，以及利用基本不等式证明不等式，属于中档题. - 26 -