高中数学第四章函数应用第1节函数与方程第2课时基础知识素材北师大版必修11 5页

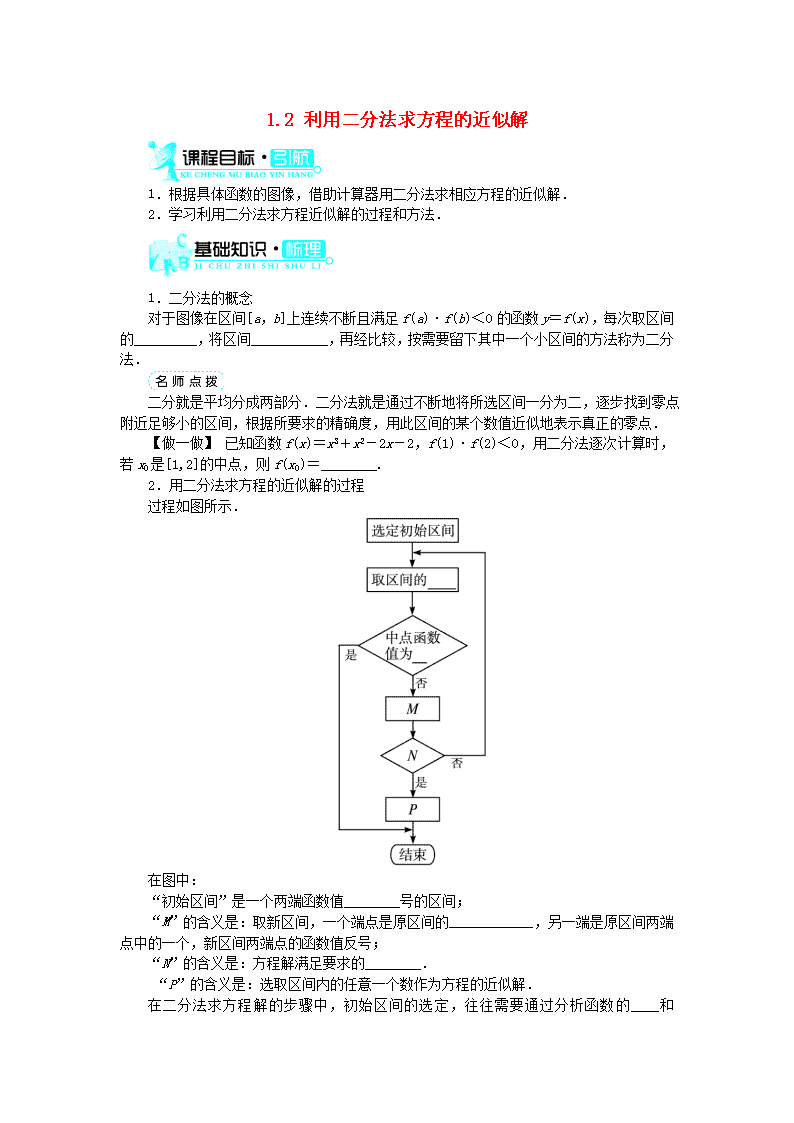
1.2 利用二分法求方程的近似解 1．根据具体函数的图像，借助计算器用二分法求相应方程的近似解． 2．学习利用二分法求方程近似解的过程和方法． 1．二分法的概念 对于图像在区间[a，b]上连续不断且满足 f(a)·f(b)＜0 的函数 y＝f(x)，每次取区间 的_________，将区间___________，再经比较，按需要留下其中一个小区间的方法称为二分 法． 二分就是平均分成两部分．二分法就是通过不断地将所选区间一分为二，逐步找到零点 附近足够小的区间，根据所要求的精确度，用此区间的某个数值近似地表示真正的零点． 【做一做】 已知函数 f(x)＝x3＋x2－2x－2，f(1)·f(2)＜0，用二分法逐次计算时， 若 x0 是[1,2]的中点，则 f(x0)＝________. 2．用二分法求方程的近似解的过程 过程如图所示． 在图中： “初始区间”是一个两端函数值________号的区间； “M”的含义是：取新区间，一个端点是原区间的____________，另一端是原区间两端 点中的一个，新区间两端点的函数值反号； “N”的含义是：方程解满足要求的________． “P”的含义是：选取区间内的任意一个数作为方程的近似解． 在二分法求方程解的步骤中，初始区间的选定，往往需要通过分析函数的____和 ___________．初始区间可以选得不同，不影响最终计算结果． 函数连续值两端，相乘为负有零点， 区间之内有一数，方程成立很显然． 要求方程近似解，先看零点的区间， 每次区间分为二，分后两端近零点． 答案：1．中点 一分为二 【做一做】 0.625 2．中点 零 反 中点 精度 性质 试验估计 用二分法求方程的近似解需注意什么？ 剖析：用二分法求方程的近似解要注意的问题： (1)要看清题目要求的精度，它决定着二分法步骤的结束． (2)初始区间的选定一般在两个整数间，不同的初始区间结果是相同的，但二分的次数 却相差较大． (3)用二分法求出的零点一般是零点的近似值，但并不是所有函数都可以用二分法求零 点，必须满足在区间[a，b]上连续不断且 f(a)·f(b)＜0 这样条件的函数才能用二分法求得 零点的近似值． 题型一 函数零点的性质 【例 1】 函数 f(x)＝x3－2x2＋3x－6 在区间[－2,4]上的零点必定在( )． A．[－2,1]内 B．[5 2 ，4]内 C．[1，7 4 ]内 D．[7 4 ，5 2 ]内 分析：按二分法的顺序是计算 f(1)，f(5 2 )等进行，但数据计算较麻烦，[－2,4]内的整 数较多，选易计算的整数求解． 反思：用二分法求函数的近似零点，是取中点求函数值，看符号，确定新区间，再取中 点求函数值等依次进行下去． 有时从计算速度上考虑，首先把整数代入计算会更快一些，如 f(0)，f(±1)，…. 题型二 求方程的近似解 【例 2】 求方程 lgx－2－x＋1＝0 的近似解(精度为 0.1)． 分析：先确定 f(x)＝lgx－2－x＋1 的零点所在的大致区间，再用二分法求解． 反思：求方程近似解的步骤：(1)构造函数，利用图像或单调性确定方程解所在的大致 区间，通常限制在区间(n，n＋1)，n∈Z；(2)利用二分法求出满足精度的方程解所在的区间 M；(3)写出方程的近似解． 题型三 用二分法证明方程根的分布 【例 3】 已知函数 f(x)＝3ax2＋2bx＋c，a＋b＋c＝0，f(0)＞0，f(1)＞0，证明 a＞0， 并利用二分法证明方程 f(x)＝0 在[0,1]内有两个实根． 分析：∵f(0)＞0，f(1)＞0， ∴只需在[0,1]内找到一个点的函数值小于零即可． 反思：根据二分法，若 f 1 2 ＜0 不成立，可计算 f 1 4 是否为负，若还不成立，再计算 f 3 4 是否为负，总之，在区间[0,1]内找到一个分点，使对应函数值为负即可． 题型四 二分法的实际应用 【例 4】 在一个风雨交加的夜里，从某水库闸房到防洪指挥部的电话线路发生了故 障．这是一条 10 km 长的线路，如何迅速查出故障所在？如果沿着线路一小段一小段地查找， 困难很多，每查一个点要爬一次电线杆，10 km 长，大约有 200 多根电线杆呢．想一想，维 修线路的工人师傅怎样工作最合理？ 分析：先检查中间一根电线杆，则将故障的范围缩小一半，再用同样方法依次检查下去． 反思：这种检查线路故障的方法，就是二分法的应用．二分法不仅可用于查找线路、水 管、气管故障，还可用于实验设计、资料查询，也是求根的常用方法． 答案：【例 1】 D 解：f(0)＝－6＜0，f(1)＝－4＜0，f(2)＝0， 故 2 为一零点在(1,3)内，只有 D 选项满足． 【例 2】 解：令 f(x)＝lgx－2－x＋1，函数 f(x)的定义域为(0，＋∞)． 因为函数 f(x)在(0，＋∞)上是增函数(证明略)，所以 f(x)至多有一个零点． 又因为 f(1)＝0.5＞0，f(0.1)≈－0.933 032 992＜0， 所以方程在[0.1,1]内有唯一一个实数解． 使用二分法求解，如下表： 次数 左端点 左端点函数值 右端点 右端点函数值 第 1 次 0.1 －0.933 032 992 1 0.5 第 2 次 0.1 －0.933 032 992 0.55 0.057 342 561 第 3 次 0.325 －0.286 415 025 0.55 0.057 342 561 第 4 次 0.437 5 －0.097 435 016 0.55 0.057 342 561 第 5 次 0.493 75 －0.016 669 624 0.55 0.057 342 561 由于区间[0.493 75,0.55]的区间长度为 0.056 25，它小于 0.1，因此，我们可以选取 这一区间内的任意一个数作为方程 lg x－2－x＋1＝0 的近似解．例如，选取 0.5 作为方程 lg x－2－x＋1＝0 的一个近似解． 【例 3】 解：∵f(1)＞0，∴3a＋2b＋c＞0， 即 3(a＋b＋c)－b－2c＞0. ∵a＋b＋c＝0， ∴－b－2c＞0，则－b－c＞c，即 a＞c. ∵f(0)＞0，∴c＞0，则 a＞0. 在[0,1]内选取二等分点1 2 ， 则 f 1 2 ＝3 4 a＋b＋c＝3 4 a＋(－a)＝－1 4 a＜0. ∵f(0)＞0，f(1)＞0， ∴f(x)在区间[0，1 2 ]和[1 2 ，1]内分别存在一个零点．又二次方程 f(x)＝0 最多有两个实 根， ∴方程 f(x)＝0 在[0,1]内有两个实根． 【例 4】 解：如图，他首先从中点 C 查．用随身带的话机向两端测试时，发现 AC 段正 常，断定故障在 BC 段，再到 BC 段中点 D，这次发现 BD 段正常，可见故障在 CD 段，再到 CD 段中点去查． 每查一次，可以把待查的线路长度缩减一半，要把故障可能发生的范围缩小到 50 m 至 100 m，即一两根电线杆附近，只要检查 7 次就够了． 1 下列图像与 x 轴均有交点，其中不能用二分法求函数零点的是( )． 2 下列函数中，必须用二分法求其零点的是( )． A．y＝x＋7 B．y＝5x－1 C．y＝log3x D．y＝ 1 2 x x     3 用二分法求函数 y＝f(x)在区间(2,4)上的零点，验证 f(2)·f(4)＜0.给定精度ε＝ 0.01，取区间(2,4)的中点 x1 ＝ 2 4 32   ，计算得 f(2)·f(x1)＜0，则此时零点 x0 ∈ __________.(填区间) 4 用二分法研究函数 f(x)＝x3＋3x－1 的零点时，第一次经计算 f(0)＜0，f(0.5)＞0， 可得其中一个零点 x0∈__________，第二次应计算__________，这时可判断 x0∈__________. 5 求方程 ln x＋x－3＝0 在(2,3)内的近似解．(精确到 0.1) 答案：1．A 2．D D 选项中无法解方程 1 02 x x      ，则必须用二分法求零点． 3．(2,3) ∵f(2)·f(3)＜0，∴x0∈(2,3)． 4．(0,0.5) f(0.25) (0.25,0.5) 由二分法知 x0∈(0,0.5)，取 x1＝0.25，这时 f(0.25) ＝0.253＋3×0.25－1＜0， 故 x0∈(0.25,0.5)． 5．分析：借助于计算器，利用二分法求解． 解：令 f(x)＝lnx＋x－3，即求函数 f(x)在(2,3)内的零点． 因为 f(2)＝ln2－1＜0，f(3)＝ln3＞0，即(2,3)作为初始区间，用二分法列表如下： 次数 左端点 左端点函数值 右端点 右端点函数值 第 1 次 2 －0.306 85 3 1.098 61 第 2 次 2 －0.306 85 2.5 0.416 29 第 3 次 2 －0.306 85 2.25 0.060 93 第 4 次 2.125 －0.121 23 2.25 0.060 93 第 5 次 2.187 5 －0.029 74 2.25 0.060 93 第 6 次 2.187 5 －0.029 74 2.218 75 0.015 69 由于区间(2.187 5,2.218 75)内所有值精确到 0.1，都是 2.2，所以方程的近似解是 2.2.