2020高中数学第二章函数4 4页

‎4.1 二次函数的图像 ‎[学业水平训练]‎ ‎1.(2014·潍坊高一检测)已知函数y＝ax2＋bx＋c的图像如图，则此函数的解析式可能为(　　)‎ A．y＝x2－x－3‎ B．y＝x2－x＋3‎ C．y＝－x2＋x－3‎ D．y＝－x2－x＋3‎ 解析：选A.由图像可知，抛物线开口向上，a＞0，顶点的横坐标为x＝－＞0，故b＜0，图像与y轴交于负半轴，故c＜0.‎ ‎2．已知a＜0，b＜0，那么抛物线y＝ax2＋bx＋2的顶点在(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 解析：‎ 选B.抛物线开口向下，顶点的横坐标为x＝－＜0，与y轴交于点(0,2)．故图像如图所示，顶点应在第二象限．‎ ‎3．用配方法将函数y＝x2－2x＋1写成y＝a(x－h)2＋ 的形式是(　　)‎ A．y＝(x－2)2－1 B．y＝(x－1)2－1‎ C．y＝(x－2)2－3 D．y＝(x－1)2－3‎ 解析：选A.y＝x2－2x＋1＝(x2－4x＋4)－1＝(x－2)2－1.‎ ‎4．已知某二次函数的图像与函数y＝2x2的图像的形状一样，开口方向相反，且其顶点为(－1,3)，则此函数的解析式为(　　)‎ A．y＝2(x－1)2＋3 B．y＝2(x＋1)2＋3‎ C．y＝－2(x－1)2＋3 D．y＝－2(x＋1)2＋3‎ 解析：选D.设所求函数的解析式为y＝a(x＋h)2＋ (a≠0)，由题意可知a＝－2，h＝1， ＝3，故y＝－2(x＋1)2＋3.‎ ‎5.二次函数f(x)＝ax2＋bx＋c(a≠0)图像如图所示，有下列结论：‎ ‎①a＋b＋c<0；‎ ‎②a－b＋c>0；‎ ‎③abc>0；‎ 4‎ ‎④b＝‎2a.‎ 其中正确结论的个数是(　　)‎ A．1 B．2‎ C．3 D．4‎ 解析：选D.由题图可得f(1)＝a＋b＋c<0，f(－1)＝a－b＋c>0，顶点的横坐标为－＝－1，∴b＝‎2a，ab>0，‎ 又f(0)＝c>0，∴abc>0.故选D.‎ ‎6．把f(x)＝2x2＋x－1的图像向右平移一个单位长度，再向下平移一个单位长度得到函数g(x)的图像，则g(x)的解析式为________．‎ 解析：由题意有g(x)＝f(x－1)－1＝2(x－1)2＋(x－1)－1－1＝2x2－3x－1.‎ 答案：2x2－3x－1‎ ‎7．已知y＝x2－4x＋h的顶点A在直线y＝－4x－1上，则二次函数解析式为________．‎ 解析：配方得y＝(x－2)2＋h－4，顶点为(2，h－4)，‎ 代入直线y＝－4x－1，得h－4＝－9，所以h＝－5.‎ 所以所求函数解析式为y＝x2－4x－5.‎ 答案：y＝x2－4x－5‎ ‎8．将抛物线y＝－3(x－1)2向上平移 个单位，所得抛物线与x轴交于两点A(x1,0)和B(x2,0)，如果x＋x＝，那么 ＝________.‎ 解析：将抛物线y＝－3(x－1)2向上平移 个单位，得抛物线y＝－3(x－1)2＋ ＝－3x2＋6x－3＋ .可知x1，x2是方程－3x2＋6x－3＋ ＝0的两实数解．所以，x1＋x2＝2，x1x2＝.又x＋x＝(x1＋x2)2－2x1x2＝4－＝，解得 ＝.‎ 答案： ‎9．(2014·江苏省启东中学月考)已知a，b为常数，且a≠0，函数f(x)＝ax2＋bx，f(2)＝0，方程f(x)＝x有两个相等的实数根．求函数f(x)的解析式．‎ 解：∵方程f(x)＝x有两个相等的实数根，且f(x)＝ax2＋bx，∴Δ＝(b－1)2＝0，∴b＝1，‎ 又f(2)＝0，∴‎4a＋2＝0，∴a＝－，‎ ‎∴f(x)＝－x2＋x.‎ ‎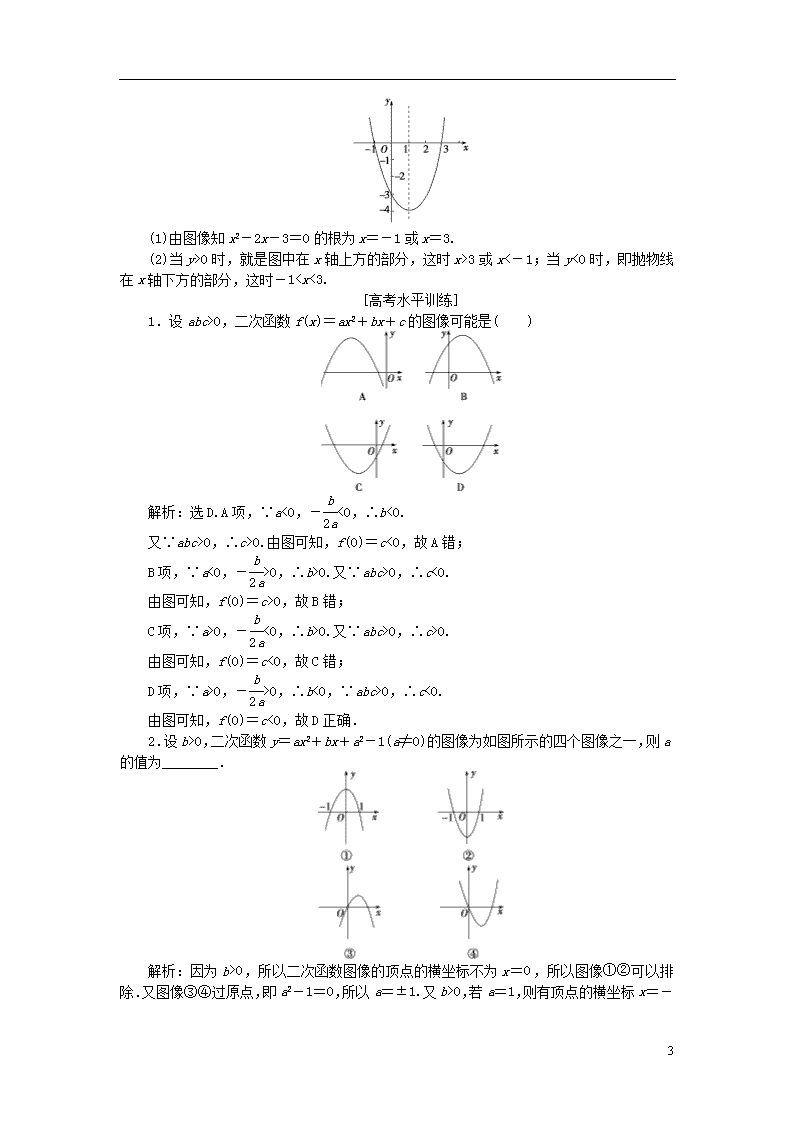10．画出函数y＝x2－2x－3的图像，并根据图像回答：‎ ‎(1)方程x2－2x－3＝0的根是什么？‎ ‎(2)x取何值时，函数值大于0？函数值小于0?‎ 解：由y＝x2－2x－3，得y＝(x－1)2－4.‎ 显然开口向上，顶点(1，－4)，与x轴交点(3,0)，(－1,0)，与y轴交点为(0，－3)，图像如图．‎ 4‎ ‎(1)由图像知x2－2x－3＝0的根为x＝－1或x＝3.‎ ‎(2)当y>0时，就是图中在x轴上方的部分，这时x>3或x<－1；当y<0时，即抛物线在x轴下方的部分，这时－10，二次函数f(x)＝ax2＋bx＋c的图像可能是(　　)‎ 解析：选D.A项，∵a<0，－<0，∴b<0.‎ 又∵abc>0，∴c>0.由图可知，f(0)＝c<0，故A错；‎ B项，∵a<0，－>0，∴b>0.又∵abc>0，∴c<0.‎ 由图可知，f(0)＝c>0，故B错；‎ C项，∵a>0，－<0，∴b>0.又∵abc>0，∴c>0.‎ 由图可知，f(0)＝c<0，故C错；‎ D项，∵a>0，－>0，∴b<0，∵abc>0，∴c<0.‎ 由图可知，f(0)＝c<0，故D正确．‎ ‎2．设b>0，二次函数y＝ax2＋bx＋a2－1(a≠0)的图像为如图所示的四个图像之一，则a的值为________．‎ 解析：因为b>0，所以二次函数图像的顶点的横坐标不为x＝0，所以图像①②可以排除．又图像③④过原点，即a2－1＝0，所以a＝±1.又b>0，若a＝1，则有顶点的横坐标x＝－<0，与图像④矛盾，所以a＝－1，且该函数的图像为③.‎ 4‎ 答案：－1‎ ‎3．当m为何值时，y＝m和y＝x2－4|x|＋5的图像有四个交点？‎ 解：画出y＝x2－4|x|＋5＝的图像，如图．‎ 再画出y＝m的图像，由图像可以看出：‎ 当1＜m＜5时，两个函数图像有四个交点．‎ ‎4．已知二次函数y＝ax2＋bx＋c(a≠0)的图像与x轴相交于点A(－3,0)，顶点的横坐标为x＝－1，顶点M到x轴的距离为2，求此函数的解析式．‎ 解：因为二次函数图像的对称轴是x＝－1，又顶点M到x轴的距离为2，所以顶点的坐标为M(－1,2)或M′(－1，－2)，‎ 故设二次函数的解析式为y＝a(x＋1)2＋2或y＝a(x＋1)2－2.‎ 因为图像过点A(－3,0)，所以0＝a(－3＋1)2＋2或0＝a(－3＋1)2－2，解得a＝－或a＝.‎ 故所求二次函数的解析式为y＝－(x＋1)2＋2＝‎ ‎－x2－x＋，或y＝(x＋1)2－2＝x2＋x－.‎ 4‎