- 248.50 KB
- 2021-06-17 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
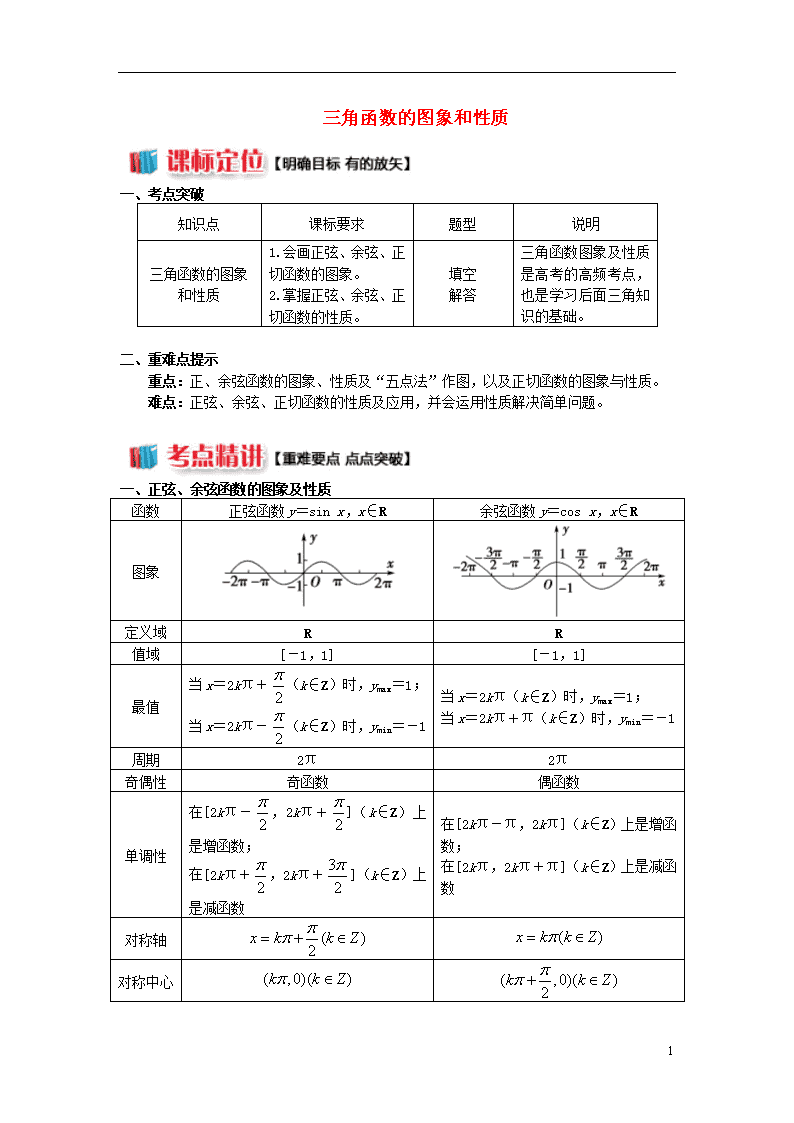
三角函数的图象和性质
一、考点突破
知识点
课标要求
题型
说明
三角函数的图象和性质
1. 会画正弦、余弦、正切函数的图象。
2. 掌握正弦、余弦、正切函数的性质。
填空
解答
三角函数图象及性质是高考的高频考点,也是学习后面三角知识的基础。
二、重难点提示
重点:正、余弦函数的图象、性质及“五点法”作图,以及正切函数的图象与性质。
难点:正弦、余弦、正切函数的性质及应用,并会运用性质解决简单问题。
一、正弦、余弦函数的图象及性质
函数
正弦函数y=sin x,x∈R
余弦函数y=cos x,x∈R
图象
定义域
R
R
值域
[-1,1]
[-1,1]
最值
当x=2kπ+(k∈Z)时,ymax=1;
当x=2kπ-(k∈Z)时,ymin=-1
当x=2kπ(k∈Z)时,ymax=1;
当x=2kπ+π(k∈Z)时,ymin=-1
周期
2π
2π
奇偶性
奇函数
偶函数
单调性
在[2kπ-,2kπ+](k∈Z)上是增函数;
在[2kπ+,2kπ+](k∈Z)上是减函数
在[2kπ-π,2kπ](k∈Z)上是增函数;
在[2kπ,2kπ+π](k∈Z)上是减函数
对称轴
对称中心
4
二、正切函数的图象及性质
函数
y=tan x
图象
定义域
{x|x≠kπ+,k∈Z}
值域
R
周期
π
奇偶性
奇函数
单调性
在(kπ-,kπ+)(k∈Z)上都是增函数
【核心突破】
①正切函数是单调递增函数,但不能说函数在定义域内是单调递增函数。
②函数其定义域由不等式得到,其周期为。
③正切函数是中心对称图形,对称中心是;不是轴对称图形,没有对称轴。
示例:
函数y=2cos(2x-)的对称中心为 。
思路分析:本题主要利用正、余弦函数的对称中心与对称轴坐标再结合整体代入的思想求解。
答案:y=cos x的对称中心为(kπ+,0)(k∈Z),
由2x-=kπ+,
得x=+π(k∈Z);
故y=2cos(2x-)的对称中心为(+π,0)(k∈Z)。
技巧点拨:牢记y=cos x的对称中心为(kπ+,0)(k∈Z),且对称中心是点,不要写成x=kπ+(k∈Z)。
4
例题1 求函数y=cos2 x+2sin x-2的值域。
思路分析:对于内外两层的复合型函数常采用换元法将其拆分成基础函数模型。故可令t=sin x,化成关于x的二次函数求解。
答案:令t=sin x(x∈R),则由-1≤sin x≤1,
知-1≤t≤1,
∴y=cos2 x+2sin x-2=-sin2x+2sin x-1
=-t2+2t-1
=-(t-1)2(-1≤t≤1),
∵-1≤t≤1,∴-2≤t-1≤0,
∴0≤(t-1)2≤4,
即-4≤y≤0,
故函数y=cos2x+2sin x-2的值域为[-4,0]。
技巧点拨:
1. 求解形如y=asin2x+bsin x+c(或y=acos2x+bcos x+c),x∈D的函数的值域或最值时,通过换元,令t=sin x(或cos x),将原函数转化为关于t的二次函数,利用配方法求值域或最值即可,求解过程中要注意t=sin x(或cos x)的有界性。
2. 求最值时要注意三角函数的定义域,在定义域内求值域,尤其要注意题目中是否给定了区间。
例题2 比较tan 1,tan 2,tan 3的大小。
思路分析:把各角化归到同一单调区间内,再利用函数的单调性进行比较。
答案:tan 2=tan(2-π),tan 3=tan(3-π),
又∵<2<π,
∴-<2-π<0,
∵<3<π,
∴-<3-π<0,
显然-<2-π<3-π<1<,
且y=tan x在(-,)内是增函数,
∴tan(2-π)<tan(3-π)<tan 1,即tan 2<tan 3<tan 1。
技巧点拨:比较三角函数值的大小时,若函数名不同,一般应先化为同名三角函数,再运用诱导公式把它们化到同一单调区间上,以便运用函数的单调性进行比较。
重视数形结合思想的运用
【满分训练】函数的图象与直线
4
有且仅有两个不同的交点,则的取值范围是 。
思路分析:该题是图象的交点的个数问题,从“图形”的角度加以解决。即画出函数图象解决。
答案:
如图,则的取值范围是。
技巧点拨:方程的根的个数和图象的交点的个数是一类问题,解决这类问题从两个角度解决。第一从方程的角度解决,即解方程,方程有几个根即有几个解或几个交点。如果方程不会解或方程含参数不好解,这时采用第二种方法,构造函数,从图形的角度解决问题。在构造函数时,往往参变分离,使其一个函数为定函数,另一个函数为简单的“动”函数。
4
相关文档
- 高中数学人教版a版选修4-4教学课件2021-06-1722页
- 2020年高中数学第二章指数函数图象2021-06-175页
- 2020版高中数学 第一章 解三角形单2021-06-179页
- 高中数学 1-2-1 几种常用函数的导2021-06-174页
- 高中数学第一章导数及其应用部分1-2021-06-1716页
- 高中数学必修5:1_示范教案(2_1_1 数2021-06-1710页
- 高中数学:新人教A版选修1-2 1_1回归2021-06-173页
- 2020高中数学集合的含义2021-06-175页
- 2019学年高中数学暑假作业 第三部2021-06-174页
- 2020年高中数学第一章导数及其应用2021-06-176页