2020高中数学 专题强化训练3 统计案例 新人教A版选修2-3 7页

专题强化训练(三) 统计案例 ‎(建议用时：45分钟)‎ ‎[基础达标练]‎ 一、选择题 ‎1．对两个分类变量A，B，下列说法中正确的个数为(　　)‎ ‎①A与B无关，即A与B互不影响；‎ ‎②A与B关系越密切，则K2的值就越大；‎ ‎③K2的大小是判定A与B是否相关的唯一依据．‎ A．1　　　B．‎2　‎　　　C．3　　　D．0‎ A　[①正确，A与B无关即A与B相互独立；②不正确，K2的值的大小只是用来检验A与B是否相互独立；③不正确，也可借助等高条形图等．故选A.]‎ ‎2．在一项中学生近视情况的调查中，某校男生150名中有80名近视，女生140名中有70名近视，在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力(　　) ‎ ‎【导学号：95032255】‎ A．平均数与方差　　　　　 B．回归分析 C．独立性检验 D．概率 C　[判断两个分类变量是否有关的最有效方法是进行独立性检验．]‎ ‎3．设某大学的女生体重y(单位：kg)与身高x(单位：cm)具有线性相关关系．根据一组样本数据(xi，yi)(i＝1,2，…，n)，用最小二乘法建立的回归方程为＝0.85x－85.71，则下列结论中不正确的是(　　)‎ A．y与x具有正的线性相关关系 B．回归直线过样本点的中心(，)‎ C．若该大学某女生身高增加‎1 cm，则其体重约增加‎0.85 kg D．若该大学某女生身高为‎170 cm，则可断定其体重必为‎58.79 kg D　[回归方程中x的系数为0.85>0，因此y与x具有正的线性相关关系，A正确；由回归方程系数的意义可知回归直线过样本点的中心(，)，B正确；依据回归方程中的含义可知，x每变化1个单位，相应变化约0.85个单位，C正确；用回归方程对总体进行估计不能得到肯定的结论，故D错误．]‎ ‎4．某校为了研究初一学生吃零食是否与性别有关，从初一年级抽取了100名学生调查购买零食的费用，规定每月在零食上花费不低于30元的为吃零食较多，每月在零食上花费不满30元的为吃零食较少．根据收集的数据得到了一个2×2列联表，并计算得出K2的观测值为k＝4.365，则下列结论正确的是(　　)‎ 7‎ A．有97.5%的把握认为“初一学生吃零食与性别有关”‎ B．有95%的把握认为“初一学生吃零食与性别有关”‎ C．该校初一学生中有95%的学生吃零食较多 D．该校初一学生中有95%的女生吃零食较多 B　[因为k＝4.365>3.841，所以有95%的把握认为“初一学生吃零食与性别有关”．]‎ ‎5．某产品的广告费用x与销售额y的统计数据如下表：‎ 广告费用x(万元)‎ ‎4‎ ‎2‎ ‎3‎ ‎5‎ 销售额y(万元)‎ ‎49‎ ‎26‎ ‎39‎ ‎54‎ 根据上表可得回归方程＝x＋中的为9.4，据此模型预报广告费用为6万元时销售额为(　　)‎ ‎ 【导学号：95032256】‎ A．63.6万元 B．65.5万元 C．67.7万元 D．72.0万元 B　[样本点的中心是(3.5,42)，则＝－＝42－9.4×3.5＝9.1，所以回归直线方程是＝9.4x＋9.1，把x＝6代入得＝65.5.]‎ 二、填空题 ‎6．面对竞争日益激烈的消费市场，众多商家不断扩大自己的销售市场，以降低生产成本．某白酒酿造企业市场部对该企业9月份的产品销量(千箱)与单位成本(百元)的资料进行线性回归分析，结果如下：＝，＝71，＝79，iyi＝1 481，‎ ＝＝－1.818 2，＝71－(－1.818 2)×≈77.36，则销量每增加1千箱，单位成本下降________元．‎ ‎181.82　[由已知可得，＝－1.818 2x＋77.36，销量每增加1千箱，则单位成本下降1.818 2百元．]‎ ‎7．在研究气温和热茶销售杯数的关系时，若求得相关指数R2≈0.85，则表明气温解释了________的热茶销售杯数变化，而随机误差贡献了剩余的________，所以气温对热茶销售杯数的效应比随机误差的效应大得多．‎ ‎85%　15%　[由相关指数R2的意义可知，R2≈0.85表明气温解释了85%，而随机误差贡献了剩余的15%.]‎ 7‎ ‎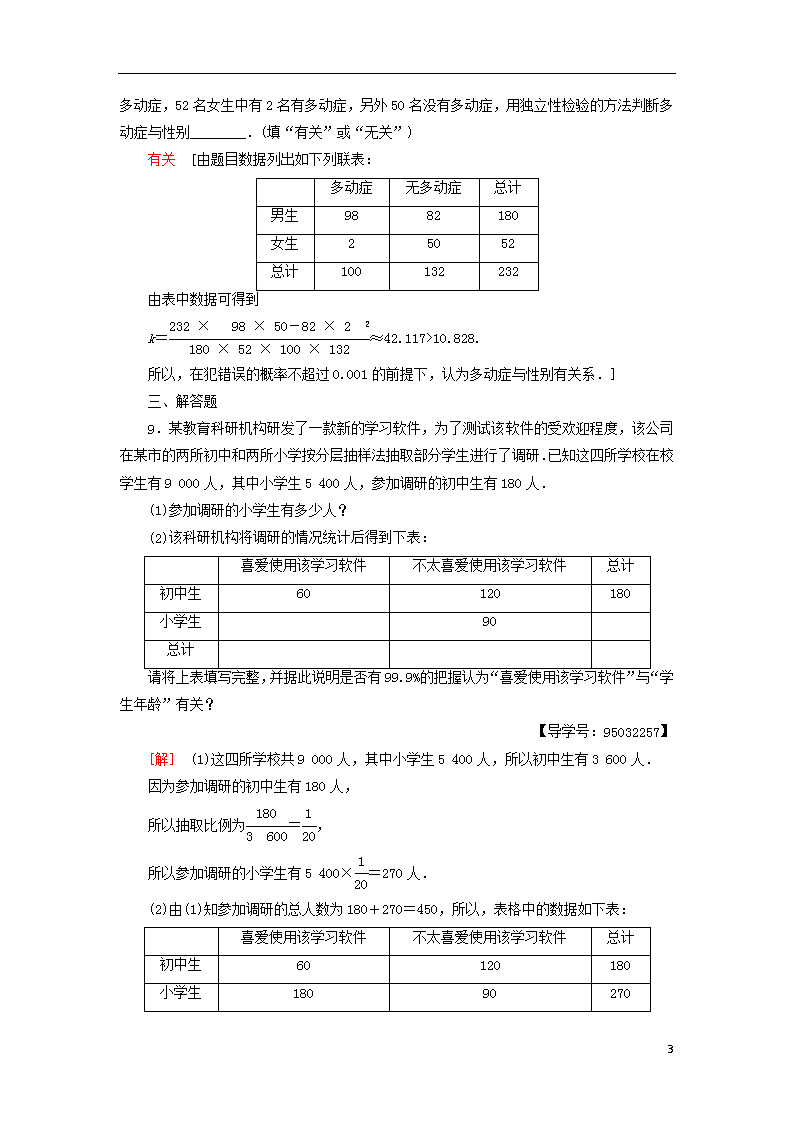8．某小学对232名小学生调查发现：180名男生中有98名有多动症，另外82名没有多动症，52名女生中有2名有多动症，另外50名没有多动症，用独立性检验的方法判断多动症与性别________．(填“有关”或“无关”)‎ 有关　[由题目数据列出如下列联表：‎ 多动症 无多动症 总计 男生 ‎98‎ ‎82‎ ‎180‎ 女生 ‎2‎ ‎50‎ ‎52‎ 总计 ‎100‎ ‎132‎ ‎232‎ 由表中数据可得到 k＝≈42.117>10.828.‎ 所以，在犯错误的概率不超过0.001的前提下，认为多动症与性别有关系．]‎ 三、解答题 ‎9．某教育科研机构研发了一款新的学习软件，为了测试该软件的受欢迎程度，该公司在某市的两所初中和两所小学按分层抽样法抽取部分学生进行了调研．已知这四所学校在校学生有9 000人，其中小学生5 400人，参加调研的初中生有180人．‎ ‎(1)参加调研的小学生有多少人？‎ ‎(2)该科研机构将调研的情况统计后得到下表：‎ 喜爱使用该学习软件 不太喜爱使用该学习软件 总计 初中生 ‎60‎ ‎120‎ ‎180‎ 小学生 ‎90‎ 总计 请将上表填写完整，并据此说明是否有99.9%的把握认为“喜爱使用该学习软件”与“学生年龄”有关？ ‎ ‎【导学号：95032257】‎ ‎[解]　(1)这四所学校共9 000人，其中小学生5 400人，所以初中生有3 600人．‎ 因为参加调研的初中生有180人，‎ 所以抽取比例为＝，‎ 所以参加调研的小学生有5 400×＝270人．‎ ‎(2)由(1)知参加调研的总人数为180＋270＝450，所以，表格中的数据如下表：‎ 喜爱使用该学习软件 不太喜爱使用该学习软件 总计 初中生 ‎60‎ ‎120‎ ‎180‎ 小学生 ‎180‎ ‎90‎ ‎270‎ 7‎ 总计 ‎240‎ ‎210‎ ‎450‎ 因为K2＝≈48.214>10.828，‎ 所以有99.9%的把握认为“喜爱玩该游戏”与“性别”有关．‎ ‎10．某班5名学生的数学和物理成绩如表：‎ A B C D E 数学成绩(x)‎ ‎88‎ ‎76‎ ‎73‎ ‎66‎ ‎63‎ 物理成绩(y)‎ ‎78‎ ‎65‎ ‎71‎ ‎64‎ ‎61‎ ‎(1)画出散点图；‎ ‎(2)求物理成绩y对数学成绩x的回归方程；‎ ‎(3)一名学生的数学成绩是96，试预测他的物理成绩. ‎ ‎【导学号：95032258】‎ ‎[解]　(1)散点图如图．‎ ‎(2)根据表中的数据，可以求得＝73.2，＝67.8，iyi＝25 054，＝27 174，‎ 所以＝≈0.625.‎ ＝－＝67.8－0.625×73.2＝22.05，‎ 所以y对x的回归方程是＝0.625x＋22.05.‎ ‎(3)＝0.625×96＋22.05≈82，‎ 可以预测他的物理成绩是82分．‎ ‎[能力提升练]‎ 一、选择题 ‎1．某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量的关系，随机抽查了52名中学生，得到统计数据如表1至表4，则与性别有关联的可能性最大的变量是(　　)‎ 7‎ A．成绩　　　　　　　 B．视力 C．智商 D．阅读量 D　[因为K＝ ‎＝，‎ K＝ ‎＝，‎ K＝ ‎＝，‎ K＝ ‎＝，‎ 则有K＞K＞K＞K，‎ 所以阅读量与性别有关联的可能性最大．]‎ ‎2．某考察团对全国10大城市进行职工人均工资水平x(千元)与居民人均消费水平y(千元)统计调查，y与x具有相关关系，回归方程为＝0.66x＋1.562，若某城市居民人均消费水平为7.675(千元)，估计该城市人均消费额占人均工资收入的百分比约为(　　) ‎ ‎【导学号：95032259】‎ 7‎ A．83% B．72%‎ C．67% D．66%‎ A　[因为当＝7.675时，x＝≈9.262，‎ 所以≈0.829≈83%.]‎ 二、填空题 ‎3．今年一轮又一轮的寒潮席卷全国．某市场为了了解某品牌羽绒服的月销售量y(件)与月平均气温x(℃)之间的关系，随机统计了某4个月的月销售量与当月平均气温，数据如下表：‎ 月平均气温x(℃)‎ ‎17‎ ‎13‎ ‎8‎ ‎2‎ 月销售量y(件)‎ ‎24‎ ‎33‎ ‎40‎ ‎55‎ 由表中数据算出线性回归方程＝x＋中的＝－2.气象部门预测下个月的平均气温约为‎6℃‎，据此估计，该商场下个月该品牌羽绒服的销售量的件数约为________．‎ ‎46　[由表格得(，)为(10,38)，又(，)在回归直线＝x＋上，且＝－2，所以38＝－2×10＋，＝58，所以＝－2x＋58，当x＝6时，＝－2×6＋58＝46.]‎ ‎4．某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：‎ 文艺节目 新闻节目 总计 ‎20至40岁 ‎40‎ ‎18‎ ‎58‎ 大于40岁 ‎15‎ ‎27‎ ‎42‎ 总计 ‎55‎ ‎45‎ ‎100‎ 由表中数据直观分析，收看新闻节目的观众是否与年龄有关：________(填“是”或“否”)．‎ 是　[因为在20至40岁的58名观众中有18名观众收看新闻节目，而大于40岁的42名观众中有27名观众收看新闻节目，即＝，＝，两者相差较大，所以经直观分析，收看新闻节目的观众与年龄是有关的．]‎ 三、解答题 ‎5．假设关于某设备的使用年限x和所支出的维修费用y(万元)，有如下表的统计资料：‎ 使用年限x ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 维修费用y ‎2.2‎ ‎3.8‎ ‎5.5‎ ‎6.5‎ ‎7.0‎ 若由资料知，y与x呈线性相关关系．‎ ‎(1)求线性回归方程＝x＋；‎ 7‎ ‎(2)求残差平方和；‎ ‎(3)求相关指数R2.‎ ‎ 【导学号：95032260】‎ ‎[解]　(1)由已知条件可得：‎ ＝4，＝5，＝90，iyi＝112.3.‎ 于是有＝＝＝1.23，‎ ＝－＝5－1.23×4＝0.08.‎ 所以＝1.23x＋0.08.‎ ‎(2)由公式i＝1.23xi＋0.08和i＝yi－i，得下表 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ i ‎2.54‎ ‎3.77‎ ‎5‎ ‎6.23‎ ‎7.46‎ i ‎－0.34‎ ‎0.03‎ ‎0.5‎ ‎0.27‎ ‎－0.46‎ 所以残差平方和为(－0.34)2＋0.032＋0.52＋0.272＋(－0.46)2＝0.651.‎ ‎(3)R2＝1－≈0.958 7.‎ 7‎