- 152.50 KB
- 2021-06-19 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
任意角、弧度
(答题时间:30分钟)
1. 把一条射线绕着端点按顺时针方向旋转240°所形成的角是________。
*2.(曲阜师大附中检测)在-720°~720°内与-1 050°角终边相同的角是________。
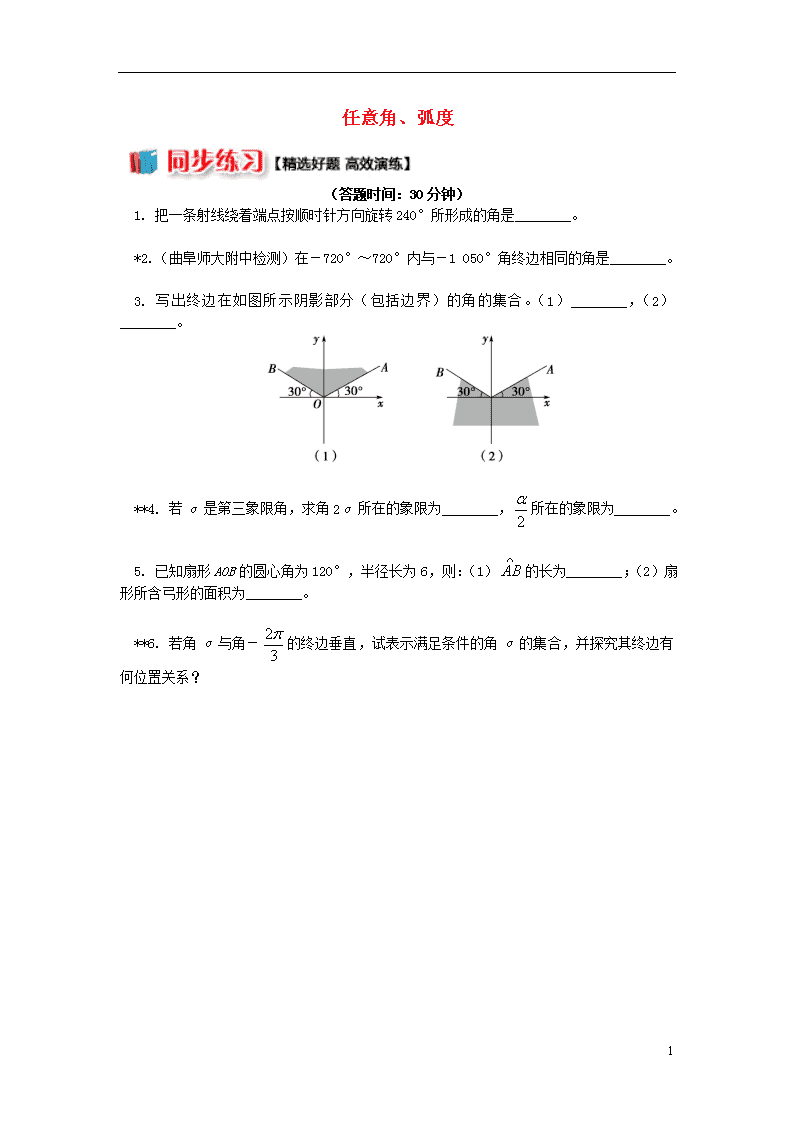
3. 写出终边在如图所示阴影部分(包括边界)的角的集合。(1)________,(2)________。
**4. 若α是第三象限角,求角2α所在的象限为________,所在的象限为________。
5. 已知扇形AOB的圆心角为120°,半径长为6,则:(1)的长为________;(2)扇形所含弓形的面积为________。
**6. 若角α与角-的终边垂直,试表示满足条件的角α的集合,并探究其终边有何位置关系?
3
1. -240° 解析:一条射线绕着端点按顺时针方向旋转所形成的角是负角,且旋转了240°,故填-240°。
2. -690°或-330°或30°或390° 解析:与-1 050°终边相同的角可表示为k·360°-1 050°(k∈Z),
k=1时,1×360°-1 050°=-690°,
k=2时,2×360°-1 050°=-330°,
k=3时,3×360°-1 050°=30°,
k=4时,4×360°-1 050°=390°。
3.(1){α|30°+k·360°≤α≤150°+k·360°,k∈Z};
(2){α|-210°+k·360°≤α≤30°+k·360°,k∈Z}
解析:先写出边界角,再按逆时针顺序写出区域角,则
(1){α|30°+k·360°≤α≤150°+k·360°,k∈Z};
(2){α|-210°+k·360°≤α≤30°+k·360°,k∈Z}
4. 第一、二象限角或终边在y轴的正半轴上的角;第二象限角或第四象限角 解析:由角α是第三象限角可知,k·360°+180°<α<k·360°+270°,k∈Z,
于是,2k·360°+360°<2α<2k·360°+540°,k∈Z,
即(2k+1)·360°<2α<(2k+1)·360°+180°,k∈Z,
所以2α为第一、二象限角或终边在y轴的正半轴上的角,
因为k·180°+90°<<k·180°+135°,k∈Z,
当k为奇数时,设k=2n+1,n∈Z,则n·360°+270°<<n·360°+315°,n∈Z,此时为第四象限角;
当k为偶数时,设k=2n,n∈Z,则n·360°+90°<<n·360°+135°,n∈Z,此时为第二象限角,
因此为第二象限角或第四象限角。
5.(1)4π(2)12π- 解析:(1)∵120°=π=π,
∴l=|α|·r=6×π=4π,
∴的长为4π;
(2)∵S扇形OAB=lr=×4π×6=12π,
如图所示,过点O作OD⊥AB,交AB于D点,
3
于是有S△OAB=×AB×OD=×2×6cos 30°×3=,
∴弓形的面积为S扇形OAB-S△OAB=12π-,
∴弓形的面积是12π-。
6. 解:在-π~π范围内,与角-的终边垂直的角为,-,与这两个角终边相同的角可分别表示为2kπ+,2kπ-,k∈Z,即{α|α=2kπ+,或α=2kπ-,k∈Z}={α|α=kπ-,k∈Z}。
所以它们的终边在同一条直线上。
3
相关文档
- 高一数学专题练习:任意角的三角函数2021-06-195页
- 专题4-1+弧度制及任意角的三角函数2021-06-198页
- 2019高三数学文北师大版一轮课时分2021-06-197页
- 高中数学必修4同步练习:任意角的三2021-06-194页
- 专题4-1+任意角和弧度制及任意角的2021-06-1913页
- 专题12+任意角和弧度制及任意角的2021-06-176页
- 高一数学(人教A版)必修4能力提升:1-1-2021-06-176页
- 高考数学热点题型和提分秘籍专题122021-06-1613页
- 高考数学一轮复习核心素养测评十九2021-06-164页
- 高中数学第7章三角函数课时分层作2021-06-165页