2013年普通高等学校招生全国统一考试数学理试题（江西卷） 9页

‎2013年普通高等学校招生全国统一考试（江西卷）‎ 理科数学 ‎ 第一卷 一、 选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．已知集合M={1,2，zi}，i，为虚数单位,N={3,4}，则复数z=‎ A.-2i B.2i C.-4i D.4i ‎2．函数y=ln(1-x)的定义域为 A．（0,1） B.[0,1) C.(0,1] D.[0,1]‎ ‎3．等比数列x，3x+3，6x+6，…..的第四项等于 A．-24 B.0 C.12 D.24‎ ‎4．总体有编号为01,02,…,19,20的20个个体组成。利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为 ‎ 7816 6572 0802 6314 0702 4369 9728 0198‎ ‎ 3204 9234 4935 8200 3623 4869 6938 7481‎ A.08 B.07 C.02 D.01‎ ‎5．(x2-)5展开式中的常数项为 A.80 B.-80 C.40 D.-40‎ ‎6．若则的大小关系为 A. B.‎ C. D.‎ ‎7．阅读如下程序框图，如果输出，那么在空白矩形框中应填入的语句为 A. B. C. D.‎ ‎8.如图，正方体的底面与正四面体的底面在同一平面上，且，正方体的六个面所在的平面与直线CE，EF相交的平面个数分别记为，那么 A.8 B.9 C.10 D.11‎ ‎9.过点引直线与曲线相交于A,B两点，O为坐标原点，当AOB的面积取最大值时，直线的斜率等于 ‎ A. B. C. D.‎ 9‎ ‎10.如图，半径为1的半圆O与等边三角形ABC夹在两平行线，之间//,与半圆相交于F,G两点，与三角形ABC两边相交于Ｅ，Ｄ两点，设弧的长为，，若从平行移动到，则函数的图像大致是 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，共20分。‎ ‎11.函数的最小正周期为为 。‎ ‎12.设，为单位向量。且，的夹角为，若，，则向量在方向上的射影为 ‎ ‎13．设函数在内可导，且，则 ‎ ‎14.抛物线的焦点为F，其准线与双曲线相交于两点，若为等边三角形，则 ‎ 三、选做题：请在下列两题中任选一题作答，若两题都做，则按第一题评阅计分，本题共5分 ‎15．（1）、（坐标系与参数方程选做题）设曲线的参数方程为（为参数），若以直角坐标系的原点为极点，轴的正半轴为极轴建立极坐标系，则曲线的极坐标方程为 ‎ ‎（2）、（不等式选做题）在实数范围内，不等式的解集为 ‎ 四．解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤。‎ ‎16.（本小题满分12分）在△ABC中，角A，B，C所对的边分别为a，b，c，已知cosC+（conA-sinA）cosB=0.‎ （1） 求角B的大小；若a+c=1，求b的取值范围 ‎17. （本小题满分12分）正项数列{an}的前项和{an}满足：‎ ‎（1）求数列{an}的通项公式an；‎ ‎（2）令，数列{bn}的前项和为。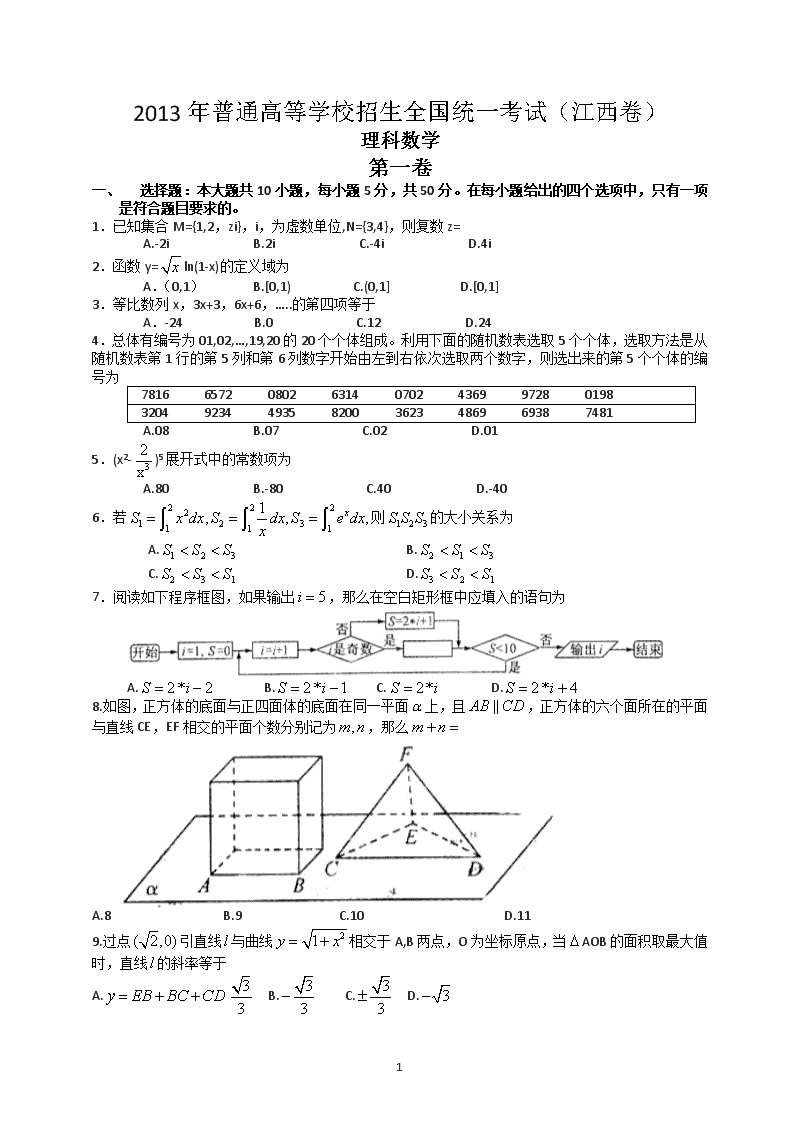证明：对于任意的，都有 9‎ ‎18.（本小题满分12分）‎ ‎ 小波以游戏方式决定参加学校合唱团还是参加学校排球队。游戏规则为：以O为起点，再从(如图)这8个点中任取两点分别为终点得到两个向量，记这两个向量的数量积为.若就参加学校合唱团，否则就参加学校排球队。‎ （1） 求小波参加学校合唱团的概率；‎ （2） 求的分布列和数学期望。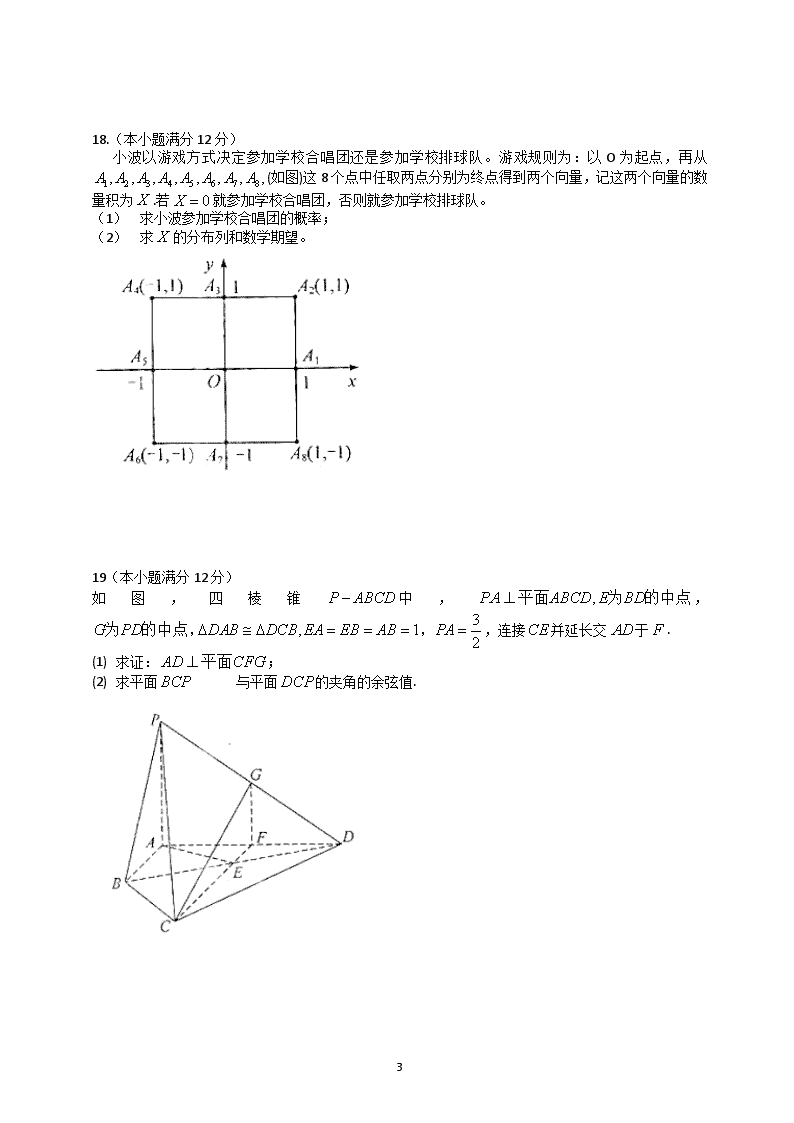‎ ‎19（本小题满分12分）‎ 如图，四棱锥中，，，连接并延长交于.‎ (1) 求证：；‎ (2) 求平面 与平面的夹角的余弦值.‎ 9‎ ‎20. (本小题满分13分) 如图，椭圆经过点离心率，直线的方程为.‎ （1） 求椭圆的方程；‎ （2） 是经过右焦点的任一弦（不经过点），设直线与直线相交于点，记的斜率分别为问：是否存在常数，使得？若存在求的值；若不存在，说明理由.‎ ‎21. (本小题满分14分)‎ ‎ 已知函数，为常数且.‎ (1) 证明：函数的图像关于直线对称；‎ (2) 若满足，但，则称为函数的二阶周期点，如果有两个二阶周期点试确定的取值范围；‎ (3) 对于（2）中的和， 设x3为函数f（f（x））的最大值点，A（x1，f（f（x1））），B（x2，f（f（x2））），C（x3，0），记△ABC的面积为S（a），讨论S（a）的单调性.‎ 9‎ ‎2013年普通高等学校招生全国统一考试（江西卷）‎ 理科数学参考答案 一、选择题：本大题共10小题，每小题5分，共50分。‎ ‎1.C 2.D 3.A 4.D 5.C 6.B 7.C 8.A 9.B 10.D 二、填空题：本大题共4小题，每小题5分，共20分。‎ ‎ 11. 12. 13. 2 14. 6‎ 三、选做题：本大题5分。‎ ‎15. （1） （2） ‎ 四、解答题：本大题共6小题，共75分。‎ ‎16. （本小题满分12分）‎ 解：（1）由已知得 ‎ 即有 ‎ 因为，所以，又，所以，‎ 又，所以。‎ ‎（2）由余弦定理，有。‎ ‎ 因为，有。‎ ‎ 又，于是有，即有。‎ ‎17.（本小题满分12分）‎ ‎（1）解：由，得。‎ 由于是正项数列，所以。‎ 于是时，。‎ 综上，数列的通项。‎ ‎（2）证明：由于。‎ 则。‎ ‎ ‎ ‎ 。 ‎ ‎18.（本小题满分12分）‎ 解：（1）从8个点中任意取两点为向量终点的不同取法共有种，时，两向量夹角为直角共有8种情形；所以小波参加学校合唱团的概率为。‎ ‎ （2）两向量数量积的所有可能取值为时，有两种情形；时，有8种情形；时，有10种情形。所以的分布列为：‎ ‎ ‎ ‎ ‎ 9‎ ‎ ‎ ‎ ‎ ‎。‎ ‎19.（本大题满分12分）‎ 解：（1）在中，因为是的中点，所以,‎ 故，‎ 因为,所以,‎ 从而有，‎ 故,又因为所以∥。‎ 又平面，‎ 所以故平面。‎ （1） 以点为坐标原点建立如图所示的坐标系，则,‎ （2） ‎，故 ‎ 设平面的法向量，则 ，‎ 解得，即。‎ 设平面的法向量，则，解得，‎ 9‎ 即。从而平面与平面的夹角的余弦值为。‎ ‎20.（本大题满分13分）‎ 解：（1）由在椭圆上得， ①‎ ‎ 依题设知，则 ②‎ ‎②代入①解得。‎ 故椭圆的方程为。‎ ‎（2）方法一：由题意可设的斜率为，‎ 则直线的方程为 ③‎ 代入椭圆方程并整理，得，‎ 设，则有 ‎ ④‎ 在方程③中令得，的坐标为。‎ 从而。‎ 注意到共线，则有，即有。‎ 所以 ‎ ‎ ⑤‎ ‎④代入⑤得，‎ 又，所以。故存在常数符合题意。‎ 方法二：设，则直线的方程为：，‎ 令，求得，‎ 从而直线的斜率为，‎ 9‎ 联立 ，得，‎ 则直线的斜率为：，直线的斜率为：，‎ 所以，‎ 故存在常数符合题意。‎ ‎21.（本大题满分14分）‎ ‎（1）证明：因为，有，‎ 所以函数的图像关于直线对称。‎ ‎（2）解：当时，有 ‎ 所以只有一个解，又，故0不是二阶周期点。‎ 当时，有 ‎ 所以有解集，又当时，，故中的所有点都不是二阶周期点。‎ 当时，有 ‎ 所以有四个解，又，‎ ‎，故只有是的二阶周期点。综上所述，所求 的取值范围为。‎ ‎（3）由（2）得，‎ 9‎ 因为为函数的最大值点，所以或。‎ 当时，。求导得：，‎ 所以当时，单调递增，当时单调递减；‎ 当时，，求导得：，‎ 因，从而有，‎ 所以当时单调递增。 ‎ ‎ ‎ 9‎