2020年高中数学第三章概率3 6页

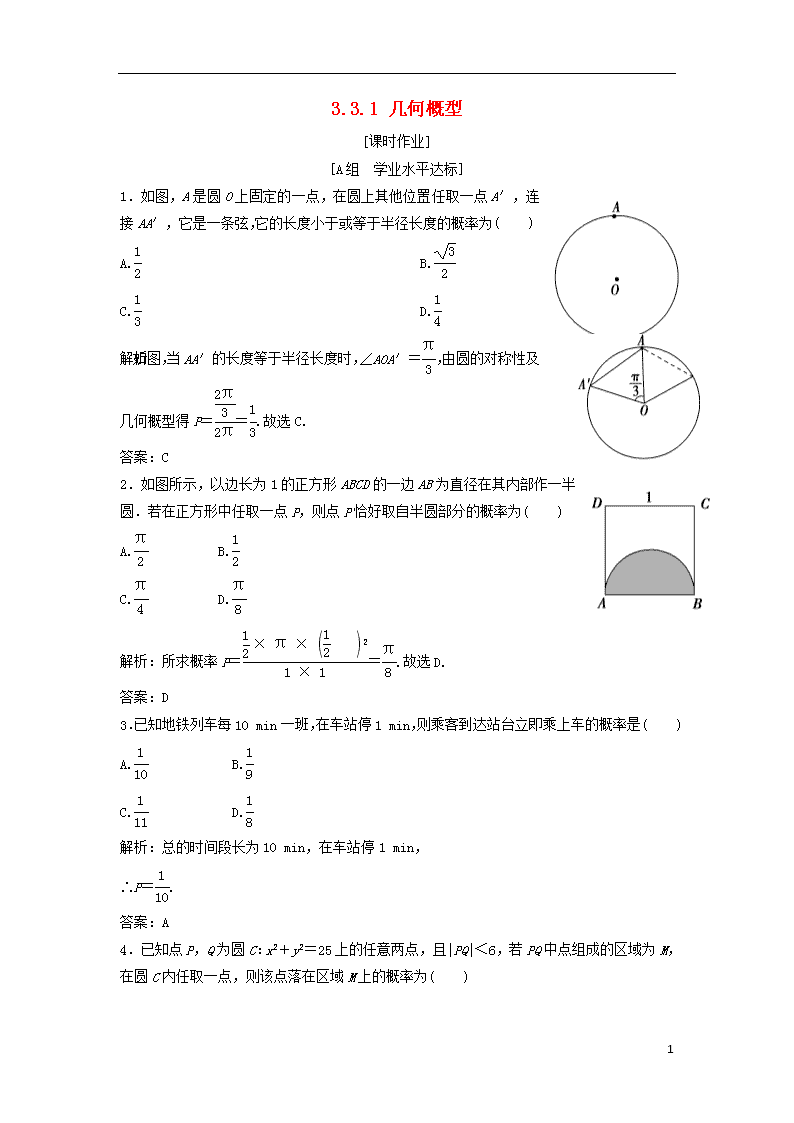
‎3.3.1‎‎ 几何概型 ‎[课时作业]‎ ‎[A组　学业水平达标]‎ ‎1．如图，A是圆O上固定的一点，在圆上其他位置任取一点A′，连接AA′，它是一条弦，它的长度小于或等于半径长度的概率为(　　)‎ A.　　　　　　　 B. C. D. 解析：如图，当AA′的长度等于半径长度时，∠AOA′＝，由圆的对称性及几何概型得P＝＝.故选C.‎ 答案：C ‎2．如图所示，以边长为1的正方形ABCD的一边AB为直径在其内部作一半圆．若在正方形中任取一点P，则点P恰好取自半圆部分的概率为(　　)‎ A. B. C. D. 解析：所求概率P＝＝.故选D.‎ 答案：D ‎3．已知地铁列车每10 min一班，在车站停1 min，则乘客到达站台立即乘上车的概率是(　　)‎ A. B. C. D. 解析：总的时间段长为10 min，在车站停1 min，‎ ‎∴P＝.‎ 答案：A ‎4．已知点P，Q为圆C：x2＋y2＝25上的任意两点，且|PQ|＜6，若PQ中点组成的区域为M，在圆C内任取一点，则该点落在区域M上的概率为(　　)‎ A. B. 6‎ C. D. 解析：PQ中点组成的区域M如图阴影部分所示，那么在C内部任取一点落在M内的概率为＝，故选B.‎ 答案：B ‎5．在区间[0,2]上随机地取一个数x，则事件“－1 (x＋)≤‎1”‎发生的概率为(　　)‎ A. B. C. D. 解析：由－1≤ (x＋)≤1得，≤log(x＋)≤，≤x＋≤2,0≤x≤，所以由几何概型概率的计算公式得，P＝＝，故选A.‎ 答案：A ‎6．点A为周长等于3的圆周上的一个定点，若在该圆周上随机取一点B，则劣弧 的长度小于1的概率为________．‎ 解析：如图可设与的长度等于1，则由几何概型可知其整体事件是其周长3，则其概率是.‎ 答案： ‎7．广告法对插播广告时间有规定，某人对某台的电视节目作了长期的统计后得出结论，他任意时间打开电视机看该台节目，看不到广告的概率约为，那么该台每小时约有________分钟广告．‎ 解析：这是一个与时间长度有关的几何概型，这人看不到广告的概率为 6‎ ‎，则看到广告的概率约为，故60×＝6.‎ 答案：6‎ ‎8．已知线段AC＝‎16 cm，先截取AB＝‎4 cm作为长方体的高，再将线段BC任意分成两段作为长方体的长和宽，则长方体的体积超过‎128 cm3的概率为________．‎ 解析：依题意，设长方体的长为x cm，则相应的宽为(12－x)cm，由4x(12－x)＞128得x2－12x＋32＜0,4＜x＜8，因此所求的概率等于＝.‎ 答案： ‎9．一个路口的红灯亮的时间为30秒，黄灯亮的时间为5秒，绿灯亮的时间为40秒，当你到达路口时，看见下列三种情况的概率各是多少？‎ ‎(1)红灯亮；(2)黄灯亮；(3)不是红灯亮．‎ 解析：在75秒内，每一时刻到达路口亮灯的时间是等可能的，属于几何概型．‎ ‎(1)P＝＝＝；‎ ‎(2)P＝＝＝；‎ ‎(3)P＝＝ ‎＝＝.‎ ‎10．在正方体ABCDA1B‎1C1D1中，棱长为1，在正方体内随机取一点M，求使MABCD的体积小于的概率．‎ 解析：设点M到面ABCD的距离为h，‎ 则VMABCD＝S底ABCD·h＝，即h＝.‎ 所以只要点M到面ABCD的距离小于时，即满足条件．‎ 所有满足点M到面ABCD的距离小于的点组成以面ABCD为底，高为的长方体，其体积为.‎ 又因为正方体体积为1，‎ 所以使四棱锥MABCD的体积小于的概率为P＝＝.‎ ‎[B组　应考能力提升]‎ ‎1．如图所示，在一个边长为a，b(a>b 6‎ ‎>0)的矩形内画一个梯形，梯形上、下底长分别为与，高为b.向该矩形内随机地投一点，则所投的点落在梯形内部的概率为(　　)‎ A. B. C. D. 解析：两“几何度量”即为两面积，直接套用几何概型的概率公式．S矩形＝ab，S梯形＝(a＋a)·b＝ab，所以所投的点落在梯形内部的概率为＝＝.‎ 答案：C ‎2．如图，矩形ABCD中，点A在x轴上，点B的坐标为(1,0)．且点C与点D在函数f(x)＝的图象上．若在矩形ABCD内随机取一点，则该点取自阴影部分的概率等于(　　)‎ A. B. C. D. ‎ 解析：由已知得B(1,0)，C(1,2)，D(－2,2)，F(0,1)，则矩形ABCD的面积为3×2＝6，阴影部分的面积为×3×1＝，故该点取自阴影部分的概率等于＝.‎ 答案：B ‎3.如图，在圆心角为90°的扇形中，以圆心O为起点作射线OC，则使得∠AOC和∠BOC都不小于30°的概率是________．‎ 解析：将圆心角为90°的扇形等分成三部分：‎ 当射线OC位于中间一部分时，使得∠AOC和∠BOC都不小于30°，‎ ‎∴使得∠AOC和∠BOC都不小于30°的概率为：‎ P＝中间部分的圆心角大小÷整个扇形的圆心角的大小＝30°÷90°＝，故使得∠AOC和∠BOC都不小于30°的概率为.‎ 6‎ 答案： ‎4．如图所示，墙上挂着一块边长为‎16 cm 的正方形木板，上面画了大、中、小三个同心圆，半径分别为‎6 cm，‎4 cm，‎2 cm.某人站在‎3 m之外向此板投镖，设投镖击中线上或没有击中木板时都不算，可重投，问：‎ ‎(1)投中大圆内的概率是多少？‎ ‎(2)投中小圆与中圆形成的圆环的概率是多少？‎ ‎(3)投中大圆之外的概率是多少？‎ 解析：整个正方形木板的面积，即基本事件所占的区域总面积D＝16×16＝256(cm2)．‎ 设“投中大圆内”为事件A，“投中小圆与中圆形成的圆环”为事件B，“投中大圆之外”为事件C，则 事件A所占区域面积为dA＝π×62＝36π(cm2)；‎ 事件B所占区域面积为 dB＝π×42－π×22＝16π－4π＝12π(cm2)；‎ 事件C所占区域面积为 dC＝D－dA＝(256－36π)(cm2)．‎ 由几何概型的概率公式，得 ‎(1)P(A)＝＝＝π，‎ 即投中大圆内的概率为π.‎ ‎(2)P(B)＝＝＝π，‎ 即投中小圆与中圆形成的圆环的概率为π.‎ ‎(3)P(C)＝＝＝1－π，‎ 即投中大圆之外的概率为1－π.‎ ‎ 5.设关于x的一元二次方程x2＋2ax＋b2＝0.‎ ‎(1)若a是从0,1,2,3四个数中任取的一个数，b是从0,1,2三个数中任取的一个数，求上述方程有实根的概率；‎ ‎(2)若a是从区间[0,3]内任取的一个数，b是从区间[0,2]内任取的一个数，求上述方程有实根的概率．‎ 解析：设事件A为“方程x2＋2ax＋b2＝0有实根”，当a≥0，b≥0时，此方程有实根的条件是(‎2a)2－4b2≥0，即a≥b.‎ 6‎ ‎(1)基本事件共有12个，分别是(0,0)，(0,1)，(0,2)，(1,0)，(1,1)，(1,2)，(2,0)，(2,1)，(2,2)，(3,0)，(3，1)，(3,2)，其中括号内第一个数表示a的取值，第二个数表示b的取值．‎ 事件A中包含9个基本事件，故事件A发生的概率为P(A)＝＝.‎ ‎(2)试验的全部结果所构成的区域为{(a，b)|0≤a≤3,0≤b≤2}，而构成事件A的区域为{(a，b)|0≤a≤3,0≤b≤2，a≥b}，即如图所示的阴影部分，所以P(A)＝＝.‎ 6‎