2020高中数学 第1章 点、直线、面的位置关系9 面面平行的判定习题 苏教版必修2 4页

面面平行的判定 ‎（答题时间：40分钟）‎ ‎*1.（郑州高一检测）正方体的六个面中互相平行的平面有_____________对。‎ ‎*2. 下列说法中正确的是_____________（填写序号即可）。‎ ‎①如果一个平面内有一条直线和另一个平面平行，那么这两个平面平行 ‎②如果一个平面内有无数条直线和另一个平面平行，那么这两个平面平行 ‎③如果一个平面内的任何直线都与另一个平面平行，那么这两个平面平行 ‎④如果两个平面平行于同一直线，则这两个平面平行 ‎**3. 在正方体EFGH－E‎1F1G1H1中，下列四对截面彼此平行的一对是_____________（填写序号即可）。‎ ‎①平面E1FG1与平面EGH1 ；②平面FHG1与平面F1H‎1G ‎③ 平面F1H1H与平面FHE1；④平面E1HG1与平面EH‎1G ‎*4.（威海高一检测）平面α与β平行的条件可能是_____________（填写序号即可）。‎ ‎①α内有无穷多条直线与β平行；②直线a∥α，a∥β ‎③直线a⊂α，直线b⊂β，且a∥β，b∥α；④α内的任何直线都与β平行 ‎**5. 平面α内有不共线的三点到平面β的距离相等且不为零，则α与β的位置关系为_____________。‎ ‎*6.（咸阳高一检测）已知直线a，平面α、β，且a∥α，a∥β，则平面α与β的位置关系是________。‎ ‎**7. 如图，已知正方体ABCD－A1B‎1C1D1，求证：平面AB1D1∥平面BDC1。‎ ‎**8. 已知点S是正三角形ABC所在平面外的一点，D、E、F分别是AC、BC、SC的中点，求证：平面DEF∥平面SAB。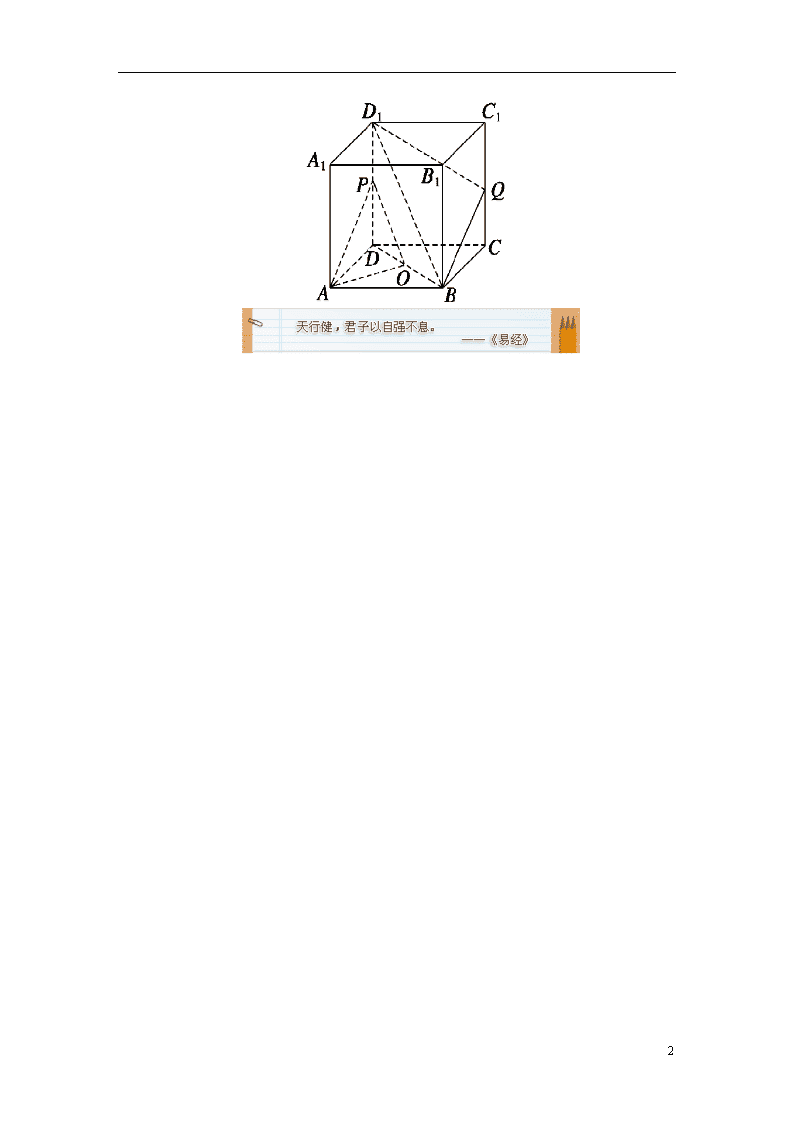‎ ‎***9. 如图，在正方体ABCD—A1B‎1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面PAO?‎ 4‎ 4‎ ‎1. 3 解析：如图，正方体ABCD－A1B‎1C1D1中，平面ABCD∥平面A1B‎1C1D1，平面ABB‎1A1∥平面CDD‎1C1，平面ADD‎1A1∥平面BCC1B1，故六个面中互相平行的平面有3对。‎ ‎2. ③ 解析：如图所示，在正方体ABCD—A1B‎1C1D1中BC∥平面A‎1C1，但平面A‎1C1与平面BC1相交，故①错误；同理平面BC1中有无数条直线与平面A‎1C1平行，但平面A‎1C1与平面BC1相交，故②错误；又AD∥平面A‎1C1，AD∥平面BC1但平面BC1与平面A‎1C1相交，故④错误。‎ ‎3. ① 解析：∵EG∥E‎1G1，EG⊄平面E1FG1，E‎1G1⊂平面E1FG1，‎ ‎∴EG∥平面E1FG1，‎ 又G‎1F∥H1E，同理可证H1E∥平面E1FG1，‎ 又H1E∩EG＝E，‎ ‎∴平面E1FG1∥平面EGH1。‎ ‎4. ④ 解析：‎ 如图①，α内可有无数条直线与β平行，但α与β相交；‎ 如图②，a∥α，a∥β，但α与β相交；‎ 如图③，a⊂α，b⊂β，a∥β，b∥α，但α与β相交。故选④。‎ ‎5. 平行或相交 解析：若三点分布于平面β的同侧，则α与β平行，若三点分布于平面β的两侧，则α与β相交。‎ 4‎ ‎6. 相交或平行 解析：因为a∥α，a∥β，所以平面α与β相交（如图1）或平行（如图2）。‎ 图1　　　　　　　　图2‎ ‎7. 证明：∵AB∥A1B1，AB＝A1B1，C1D1∥A1B1，C1D1＝A1B1，‎ ‎∴AB∥C1D1，AB＝C1D1，‎ ‎∴四边形ABC1D1为平行四边形，‎ ‎∴AD1∥BC1，‎ 又AD1⊂平面AB1D1，BC1⊄平面AB1D1，‎ ‎∴BC1∥平面AB1D1，同理，BD∥平面AB1D1，‎ 又BD∩BC1＝B，∴平面AB1D1∥平面C1BD。‎ ‎8. 证明：∵E、F分别为BC、SC的中点，‎ ‎∴EF为△SBC的中位线，则EF∥SB，‎ ‎∵EF⊄平面SAB，SB⊂平面SAB，‎ ‎∴EF∥平面SAB，‎ 同理DF∥平面SAB，‎ 又∵EF∩DF＝F，且EF⊂平面DEF，DF⊂平面DEF，‎ ‎∴平面DEF∥平面SAB。‎ ‎9. 解：当Q为CC1的中点时，平面D1BQ∥平面PAO。证明如下：‎ ‎∵Q为CC1的中点，P为DD1的中点，‎ ‎∴QB∥PA，‎ ‎∵P、O分别为DD1、DB的中点，∴D1B∥PO，‎ 又∵D1B⊄平面PAO，PO⊂平面PAO，‎ QB⊄平面PAO，PA⊂平面PAO，‎ ‎∴D1B∥平面PAO，QB∥平面PAO，‎ 又D1B∩QB＝B，D1B、QB⊂平面D1BQ，‎ ‎∴平面D1BQ∥平面PAO。‎ 4‎