高中数学必修1教案：第二章（第16课时）指数函数3 4页

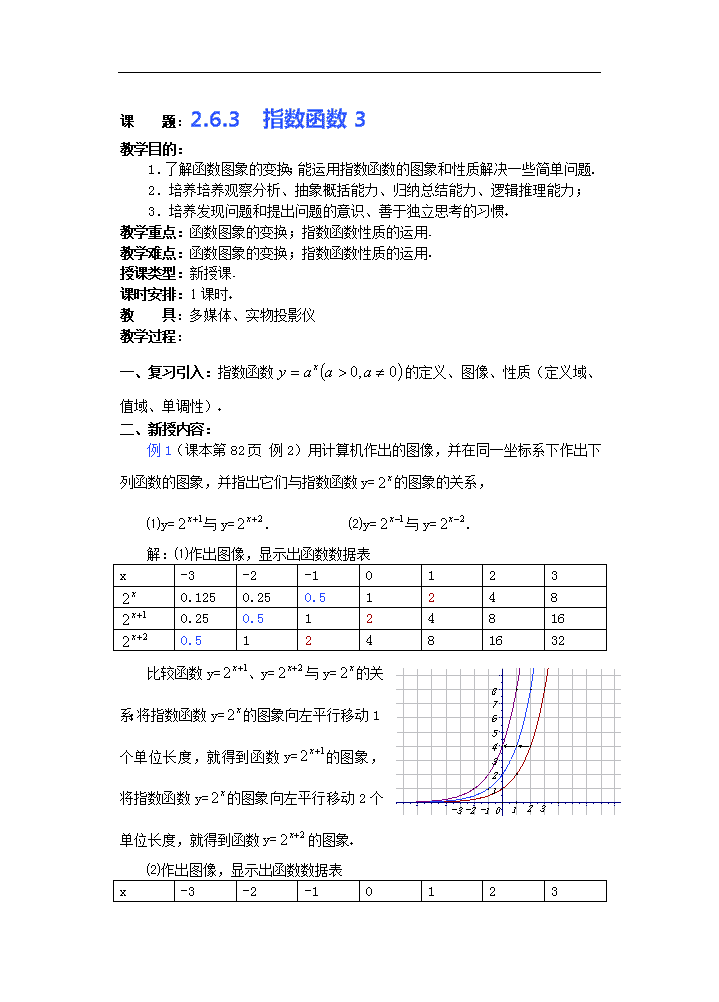
课 题：2.6.3 指数函数3‎ 教学目的： ‎ ‎1．了解函数图象的变换；能运用指数函数的图象和性质解决一些简单问题.‎ ‎2．培养培养观察分析、抽象概括能力、归纳总结能力、逻辑推理能力；‎ ‎3．培养发现问题和提出问题的意识、善于独立思考的习惯 ‎ 教学重点：函数图象的变换；指数函数性质的运用 教学难点：函数图象的变换；指数函数性质的运用.‎ 授课类型：新授课 课时安排：1课时 教 具：多媒体、实物投影仪 教学过程：‎ 一、复习引入：指数函数的定义、图像、性质（定义域、值域、单调性）‎ 二、新授内容：‎ 例1（课本第82页 例2）用计算机作出的图像，并在同一坐标系下作出下列函数的图象，并指出它们与指数函数y=的图象的关系，‎ ‎⑴y=与y=. ⑵y=与y=.‎ 解：⑴作出图像，显示出函数数据表 x ‎-3‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎0.125‎ ‎0.25‎ ‎0.5‎ ‎1‎ ‎2‎ ‎4‎ ‎8‎ ‎0.25‎ ‎0.5‎ ‎1‎ ‎2‎ ‎4‎ ‎8‎ ‎16‎ ‎0.5‎ ‎1‎ ‎2‎ ‎4‎ ‎8‎ ‎16‎ ‎32‎ 比较函数y=、y=与y=的关系：将指数函数y=的图象向左平行移动1个单位长度，就得到函数y=的图象，将指数函数y=的图象向左平行移动2个单位长度，就得到函数y=的图象 ‎⑵作出图像，显示出函数数据表 x ‎-3‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎0.125‎ ‎0.25‎ ‎0.5‎ ‎1‎ ‎2‎ ‎4‎ ‎8‎ ‎0.625‎ ‎0.125‎ ‎0.25‎ ‎0.5‎ ‎1‎ ‎2‎ ‎4‎ ‎0.3125‎ ‎0.625‎ ‎0.125‎ ‎0.25‎ ‎0.5‎ ‎1‎ ‎2‎ 比较函数y=、y=与y=的关系：将指数函数y=的图象向右平行移动1个单位长度，就得到函数y=的图象，将指数函数y=的图象向右平行移动2个单位长度，就得到函数y=的图象 小结：⑴ y=与y=的关系：当m>0时，将指数函数y=的图象向右平行移动m个单位长度，就得到函数y=的图象；当m<0时，将指数函数y=的图象向左平行移动m个单位长度，就得到函数y=的图象 例2 ⑴已知函数 用计算器或计算机作出函数图像，求定义域、值域，并探讨与图像的关系 ‎ 解： 定义域：xÎR 值域： ‎ 关系：将的图像y轴右侧的部分翻折到y轴左侧的到的图像，关于y轴对称.‎ ‎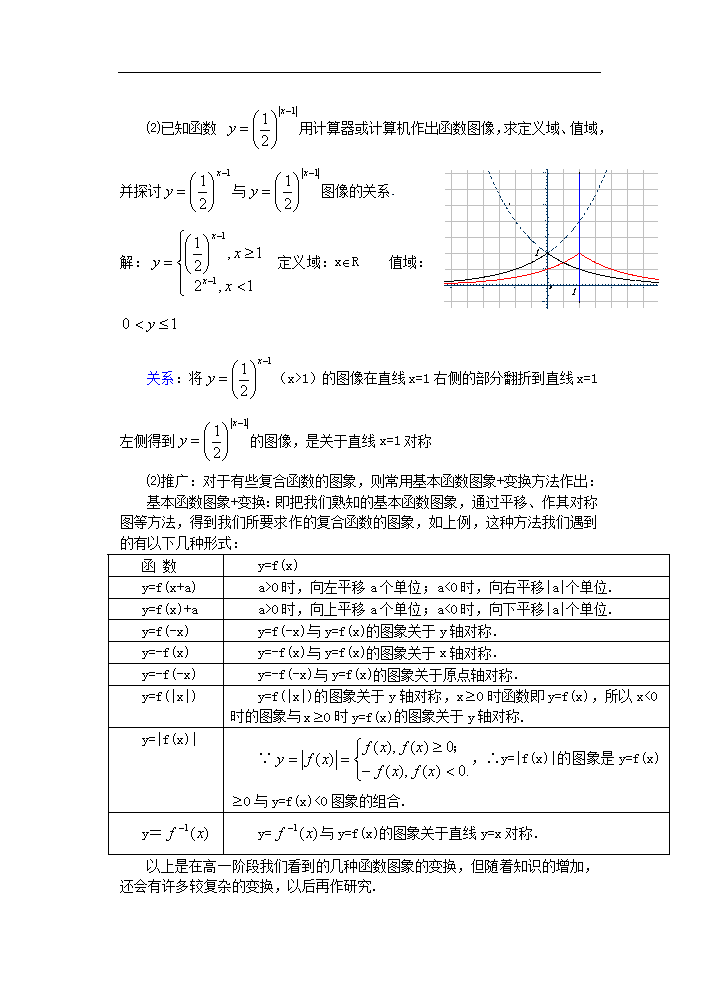⑵已知函数 用计算器或计算机作出函数图像，求定义域、值域，并探讨与图像的关系 解： 定义域：xÎR 值域：‎ 关系：将（x>1）的图像在直线x=1右侧的部分翻折到直线x=1左侧得到的图像，是关于直线x=1对称 ‎⑵推广：对于有些复合函数的图象，则常用基本函数图象+变换方法作出：‎ 基本函数图象+变换：即把我们熟知的基本函数图象，通过平移、作其对称图等方法，得到我们所要求作的复合函数的图象，如上例，这种方法我们遇到的有以下几种形式：‎ 函 数 y=f(x)‎ y=f(x+a)‎ a>0时，向左平移a个单位；a<0时，向右平移|a|个单位.‎ y=f(x)+a a>0时，向上平移a个单位；a<0时，向下平移|a|个单位.‎ y=f(-x)‎ y=f(-x)与y=f(x)的图象关于y轴对称.‎ y=-f(x)‎ y=-f(x)与y=f(x)的图象关于x轴对称.‎ y=-f(-x)‎ y=-f(-x)与y=f(x)的图象关于原点轴对称.‎ y=f(|x|)‎ y=f(|x|)的图象关于y轴对称，x0时函数即y=f(x)，所以x<0时的图象与x0时y=f(x)的图象关于y轴对称.‎ y=|f(x)|‎ ‎∵，∴y=|f(x)|的图象是y=f(x)0与y=f(x)<0图象的组合.‎ y＝‎ y=与y=f(x)的图象关于直线y=x对称.‎ 以上是在高一阶段我们看到的几种函数图象的变换，但随着知识的增加，还会有许多较复杂的变换，以后再作研究.‎ 例3探讨函数和 的图象的关系，并证明关 于y轴对称 ‎ ‎ 证：设P(,)是函数 的图象上任意一点 ‎ 则 而P(,)关于y轴的对称点Q是(-,)‎ ‎ ∴ 即Q在函数的图象上 ‎ 由于P是任意取的,所以上任一点关于y轴的对称点都在的图象上 ‎ 同理可证： 图象上任意一点也一定在函数的图象上 ‎ ∴ 函数和的图象关于y轴对称 例4 已知函数 求函数的定义域、值域 解：作出函数图像，观察分析讨论，教师引导、整理 定义域为 R 由得 ‎ ‎∵xÎR, ∴△0, 即 , ∴, 又∵，∴‎ 三、小结 本节课学习了以下内容：函数图像的变换 四、课后作业：‎ 五、板书设计（略）‎ 六、课后记：‎