2020高中数学 课时分层作业18 空间向量与平行关系 新人教A版选修2-1 6页

课时分层作业(十八) 空间向量与平行关系 ‎(建议用时：40分钟)‎ ‎[基础达标练]‎ 一、选择题 ‎1．已知直线l的方向向量是a＝(3,2,1)，平面α的法向量是u＝(－1,2，－1)，则l与α的位置关系是(　　)‎ A．l⊥α　　　　　　 B．l∥α C．l与α相交但不垂直 D．l∥α或l⊂α D　[因为a·u＝－3＋4－1＝0，所以a⊥u，所以l∥α或l⊂α.]‎ ‎2．已知A(0，y,3)，B(－1，－2，z)，若直线l的方向向量v＝(2,1,3)与直线AB的方向向量平行，则y＋z等于(　　)‎ A．－3　 B．‎0　‎　　C．1　　　D．3‎ B　[由题意，得＝(－1，－2－y，z－3)，则＝＝，解得y＝－，z＝，所以y＋z＝0，故选B．]‎ ‎3．已知平面α内有一个点A(2，－1,2)，α的一个法向量为n＝(3,1,2)，则下列点P中，在平面α内的是(　　)‎ A．(1，－1,1) B． C． D． B　[对于B，＝，‎ 则n·＝(3,1,2)·＝0，‎ ‎∴n⊥，则点P在平面α内．]‎ ‎4．若＝λ＋μ，则直线AB与平面CDE的位置关系是(　　) ‎ ‎【导学号：46342164】‎ A．相交 B．平行 C．在平面内 D．平行或在平面内 D　[∵＝λ＋μ，∴，，共面，则AB与平面CDE的位置关系是平行或在平面内．]‎ 6‎ ‎5．若平面α，β的一个法向量分别为m＝，n＝，则(　　)‎ A．α∥β B．α⊥β C．α与β相交但不垂直 D．α∥β或α与β重合 D　[因为n＝－‎3m，所以m∥n，因此α∥β或α与β重合．]‎ 二、填空题 ‎6．如图325，在正三棱锥SABC中，点O是△ABC的外心，点D是棱BC的中点，则平面ABC的一个法向量可以是________，平面SAD的一个法向量可以是________．‎ 图325‎ ，　[由题意知SO⊥平面ABC，BC⊥平面SAD．‎ 因此平面ABC的一个法向量可以是，平面SAD的一个法向量可以是.]‎ ‎7．若a＝(2x,1,3)，b＝(1，－2y,9)，且a与b为共线向量，则x＝________，y＝________.‎ 　－　[由题意得＝＝，∴x＝，y＝－.]‎ ‎8．已知直线l∥平面ABC，且l的一个方向向量为a＝(2，m,1)，A(0,0,1)，B(1,0,0)，C(0,1,0)，则实数m的值是________. 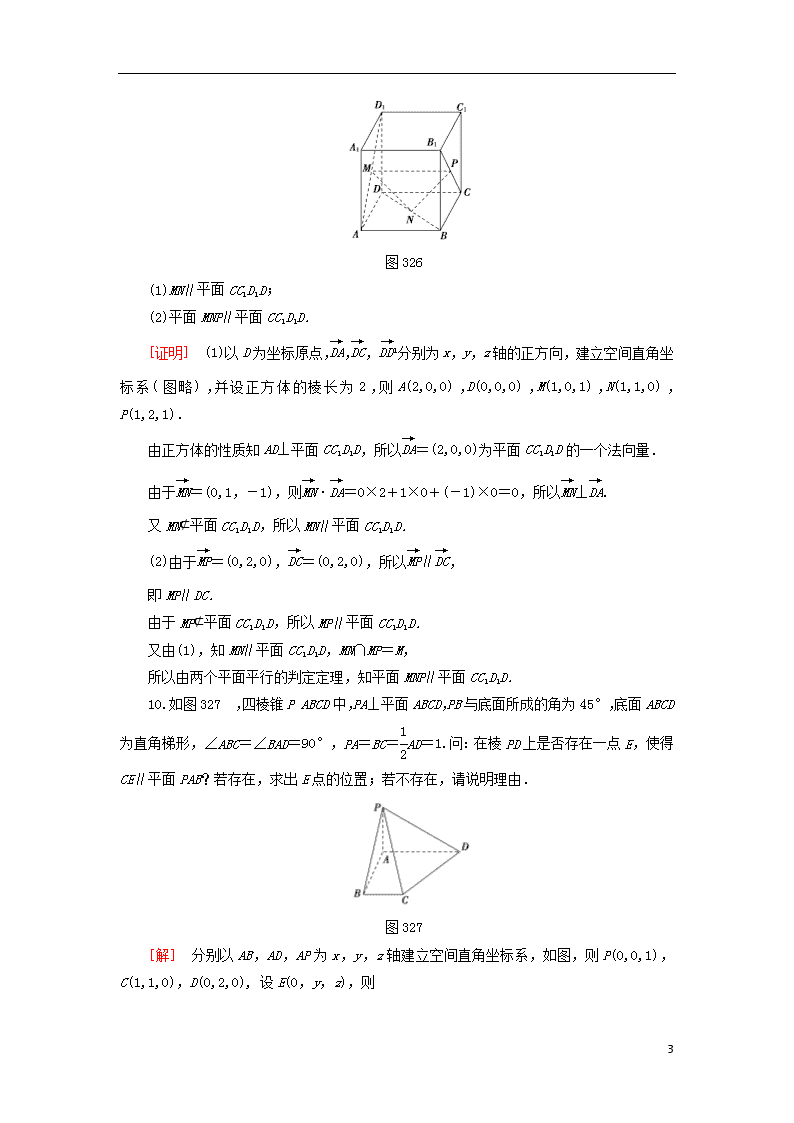‎ ‎【导学号：46342165】‎ ‎－3　[∵l∥平面ABC，‎ ‎∴存在实数x，y，使a＝x＋y，＝(1,0，－1)，＝(0,1，－1)，‎ ‎∴(2，m,1)＝x(1,0，－1)＋y(0,1，－1)‎ ‎＝(x，y，－x－y)，‎ ‎∴∴m＝－3.]‎ 三、解答题 ‎9．如图326，在正方体ABCDA1B‎1C1D1中，M，N，P分别是AD1，BD和B‎1C的中点，利用向量法证明：‎ 6‎ 图326‎ ‎(1)MN∥平面CC1D1D；‎ ‎(2)平面MNP∥平面CC1D1D．‎ ‎[证明]　(1)以D为坐标原点，，，分别为x，y，z轴的正方向，建立空间直角坐标系(图略)，并设正方体的棱长为2，则A(2,0,0)，D(0,0,0)，M(1,0,1)，N(1,1,0)，P(1,2,1)．‎ 由正方体的性质知AD⊥平面CC1D1D，所以＝(2,0,0)为平面CC1D1D的一个法向量．‎ 由于＝(0,1，－1)，则·＝0×2＋1×0＋(－1)×0＝0，所以⊥.‎ 又MN⊄平面CC1D1D，所以MN∥平面CC1D1D．‎ ‎(2)由于＝(0,2,0)，＝(0,2,0)，所以∥，‎ 即MP∥DC．‎ 由于MP⊄平面CC1D1D，所以MP∥平面CC1D1D．‎ 又由(1)，知MN∥平面CC1D1D，MN∩MP＝M，‎ 所以由两个平面平行的判定定理，知平面MNP∥平面CC1D1D．‎ ‎10.如图327，四棱锥PABCD中，PA⊥平面ABCD，PB与底面所成的角为45°，底面ABCD为直角梯形，∠ABC＝∠BAD＝90°，PA＝BC＝AD＝1.问：在棱PD上是否存在一点E，使得CE∥平面PAB？若存在，求出E点的位置；若不存在，请说明理由．‎ 图327‎ ‎[解]　分别以AB，AD，AP为x，y，z轴建立空间直角坐标系，如图，则P(0,0,1)，C(1,1,0)，D(0,2,0), 设E(0，y，z)，则 6‎ ＝(0，y，z－1)，＝(0,2，－1)，‎ ‎∵∥，∴y(－1)－2(z－1)＝0，①‎ ‎∵＝(0,2,0)是平面PAB的法向量，‎ ＝(－1，y－1，z)，‎ ‎∴由CE∥平面PAB, 可得⊥，‎ ‎∴(－1，y－1，z)·(0,2,0)＝2(y－1)＝0，‎ ‎∴y＝1，代入①式得z＝.∴E是PD的中点，‎ 即存在点E为PD中点时，CE∥平面PAB．‎ ‎[能力提升练]‎ ‎1．若a＝是平面α的一个法向量，且b＝(－1,2,1)，c＝与平面α都平行，则向量a等于(　　)‎ A． B． C． D． D　[由题意，知a·b＝0，a·c＝0，即，‎ 解得，所以a＝.]‎ ‎2．已知＝(－3,1,2)，平面α的一个法向量为n＝(2，－2,4)，点A不在平面α内，则直线AB与平面α的位置关系为(　　)‎ A．AB⊥α B．AB⊂α 6‎ C．AB与α相交但不垂直 D．AB∥α D　[因为n·＝2×(－3)＋(－2)×1＋4×2＝0，所以n⊥.又点A不在平面α内，n为平面α的一个法向量，所以AB∥α，故选D．]‎ ‎3．若A，B，C是平面α内的三点，设平面α的法向量a＝(x，y，z)，则x∶y∶z＝________. ‎ ‎【导学号：46342166】‎ ‎2∶3∶(－4)　[因为＝，‎ ＝，‎ 又因为a·＝0，a·＝0，‎ 所以 解得 所以x∶y∶z＝y∶y∶＝2∶3∶(－4)．]‎ ‎4．如图328，在长方体ABCDA1B‎1C1D1中，AA1＝AD＝1，E为CD的中点，点P在棱AA1上，且DP∥平面B1AE，则AP的长为________．‎ 图328‎ 　[建立以AB，AD，AA1所在直线分别为x，y，z轴的空间直角坐标系(图略)，‎ 设|AB|＝a，点P坐标为(0,0，b)‎ 则B1(a,0,1)，D(0,1,0)，E ＝(a,0,1)，＝ ＝(0，－1，b)，∵DP∥平面B1AE，‎ ‎∴存在实数λ，μ，设＝λ＋μ 6‎ 即(0，－1，b)＝λ(a,0,1)＋μ ‎＝ ‎∴∴b＝λ＝，即AP＝.]‎ ‎5．如图329，在正方体ABCDA1B‎1C1D1中，O为底面ABCD的中心，P是DD1的中点．设Q是CC1上的点，则当点Q在什么位置时，平面D1BQ∥平面PAO?‎ 图329‎ ‎[解]　建立如图所示的空间直角坐标系Dxyz，设正方体的棱长为2，‎ 则O(1,1,0)，A(2,0,0)，P(0,0,1)，B(2,2,0)，D1(0,0,2)，‎ ‎∴＝(1，－1,0)，＝(－1，－1,1)，＝(－2，－2，2)．‎ 设平面PAO的法向量为n1＝(x，y，z)，‎ 则，即 令x＝1，则y＝1，z＝2，‎ ‎∴平面PAO的一个法向量为n1＝(1,1,2)．‎ 若平面D1BQ∥平面PAO，则n1也是平面D1BQ的一个法向量．‎ 设Q(0,2，c)，则＝(－2,0，c)，‎ ‎∴n1·＝0，即－2＋‎2c＝0，∴c＝1，‎ 这时n1·＝－2－2＋4＝0.‎ ‎∴当Q为CC1的中点时，平面D1BQ∥平面PAO.‎ 6‎