2020年高中数学第二章推理与证明2 6页

‎2.1.1‎‎ 合情推理 ‎[课时作业]‎ ‎[A组　基础巩固]‎ ‎1．观察下列各式：72＝49,73＝343,74＝2401，…，则72 015的末两位数字为(　　)‎ A．01　　　　　　　　 B．43‎ C．07 D．49‎ 解析：因为71＝7,72＝49,73＝343,74＝2 401,75＝16 807，76＝117 649，…，‎ 所以这些数的末两位数字呈周期性出现，且周期T＝4.‎ 又2 015＝4×503＋3，‎ 所以72 015的末两位数字与73的末两位数字相同，为43.‎ 答案：B ‎2．下面几种推理是合情推理的是(　　)‎ ‎①由圆的性质类比出球的有关性质；‎ ‎②由直角三角形、等腰三角形、等边三角形的内角和是180°，归纳出所有三角形的内角和都是180°；‎ ‎③张军某次考试成绩是100分，由此推出全班同学的成绩都是100分；‎ ‎④三角形内角和是180°，四边形内角和是360°，五边形内角和是540°，由此得凸多边形内角和是(n－2)·180°.‎ A．①② B．①③ ‎ C．①②④ D．②④‎ 解析：①是类比推理；②是归纳推理；④是归纳推理．所以①、②、④是合情推理．‎ 答案：C ‎3．已知{bn}为等比数列，b5＝2，则b1b2b3…b9＝29.若{an}为等差数列，a5＝2，则{an}的类似结论为(　　)‎ A．a‎1a2a3…a9＝29 B．a1＋a2＋…＋a9＝29‎ C．a‎1a2…a9＝2×9 D．a1＋a2＋…＋a9＝2×9‎ 解析：等比数列中积等差数列中的和 ‎∴a1＋a2＋…＋a9＝2×9.‎ 答案：D ‎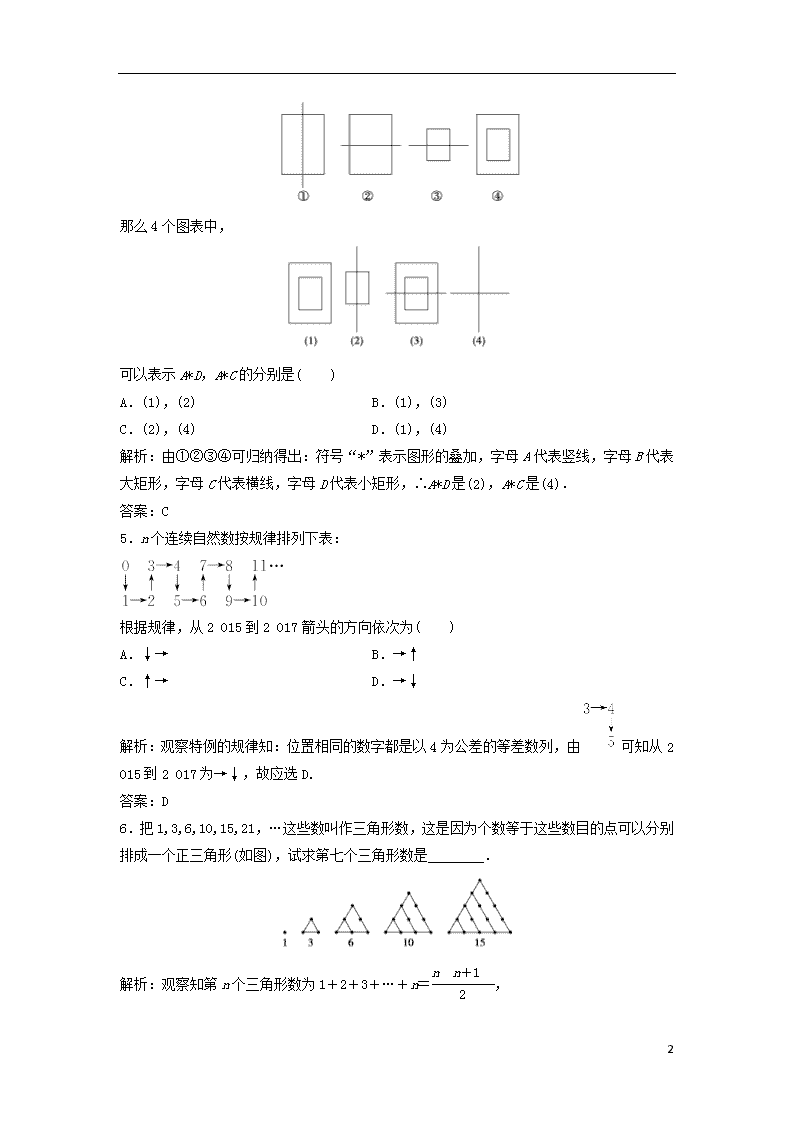4．定义A*B，B*C，C*D，D*B依次对应4个图形：‎ 6‎ 那么4个图表中，‎ 可以表示A*D，A*C的分别是(　　)‎ A．(1)，(2) B．(1)，(3)‎ C．(2)，(4) D．(1)，(4)‎ 解析：由①②③④可归纳得出：符号“*”表示图形的叠加，字母A代表竖线，字母B代表大矩形，字母C代表横线，字母D代表小矩形，∴A*D是(2)，A*C是(4)．‎ 答案：C ‎5．n个连续自然数按规律排列下表：‎ 根据规律，从2 015到2 017箭头的方向依次为(　　)‎ A．↓→ B．→↑‎ C．↑→ D．→↓‎ 解析：观察特例的规律知：位置相同的数字都是以4为公差的等差数列，由可知从2 015到2 017为→↓，故应选D.‎ 答案：D ‎6．把1,3,6,10,15,21，…这些数叫作三角形数，这是因为个数等于这些数目的点可以分别排成一个正三角形(如图)，试求第七个三角形数是________．‎ 解析：观察知第n个三角形数为1＋2＋3＋…＋n＝，‎ 6‎ ‎∴第7个三角形数为＝28.‎ 答案：28‎ ‎7．在平面上，若两个正三角形的边长比为1∶2.则它们的面积比为1∶4.类似地，在空间中，若两个正四面体的棱长比为1∶2，则它们的体积比为________．‎ 解析：＝＝·＝×＝.‎ 答案：1∶8‎ ‎8．设函数f(x)＝(x>0)，‎ 观察：f1(x)＝f(x)＝，‎ f2(x)＝f(f1(x))＝，‎ f3(x)＝f(f2(x))＝，‎ f4(x)＝f(f3(x))＝，……‎ 根据以上事实，由归纳推理可得：当n∈N*且n≥2时，fn(x)＝f(fn－1(x))＝________.‎ 解析：根据题意知，分子都是x，分母中的常数项依次是2,4,8,16，…可知fn(x)的分母中常数项为2n，分母中x的系数为2n－1，故fn(x)＝.‎ 答案： ‎9．在平面几何里，有勾股定理：“设△ABC的两边AB，AC互相垂直，则AB2＋AC2＝BC‎2”‎，拓展到空间，类比平面几何的勾股定理，研究三棱锥的侧面积与底面积间的关系， 给出正确结论．‎ 解析：由平面直角三角形类比空间三棱锥由边垂直侧面垂直．‎ 直角三角形的“直角边长、斜边长”类比“三棱锥的侧面积、底面积”，因此类比的结论是：“设三棱锥ABCD的三个侧面ABC、ACD、ABD两两相互垂直，则S＋S＋S＝S”．‎ ‎10．已知数列{an}的第1项a1＝1，且an＋1＝(n＝1,2，…)，试归纳出这个数列的通项公式．‎ 解析：当n＝1时，a1＝1‎ 6‎ 当n＝2时，a2＝＝；‎ 当n＝3时，a3＝＝；‎ 当n＝4时，a4＝＝.‎ 观察可得，数列的前4项都等于相应序号的倒数，由此猜想，这个数列的通项公式为：an＝(n＝1,2，…)．‎ ‎[B组　能力提升]‎ ‎1．已知数列{an}满足an＋1＝an－an－1(n≥2)，a1＝a，a2＝b，设Sn＝a1＋a2＋…＋an，则下列结论正确的是(　　)‎ A．a100＝－a，S100＝2b－a B．a100＝－b，S100＝2b－a C． a100＝－b，S100＝b－a D．a100＝－a，S100＝b－a 解析：∵a1＝a，a2＝b，a3＝b－a，a4＝－a，a5＝－b，a6＝a－b.‎ 且a7＝a6－a5＝a，a8＝b，…，‎ ‎∴数列{an}具有周期性，周期为6，且S6＝0‎ 则a100＝a4＝－a，S100＝S4＝2b－a.‎ 答案：A ‎2．类比平面内正三角形的“三边相等，三内角相等”的性质，可推知正四面体的下列性质，你认为比较恰当的是(　　)‎ ‎①各棱长相等，同一顶点上的任意两条棱的夹角相等；‎ ‎②各个面是全等的正三角形，相邻的两个面所成的二面角相等；‎ ‎③各个面是全等的正三角形，同一顶点上的任意两条棱的夹角相等；‎ ‎④各棱长相等，相邻的两个面所成的二面角相等．‎ A．①④ B．①②‎ C．①③ D．③④‎ 解析：类比推理的原则是：类比前后保持类比规则的一致性，而③④违背了这一原则，只有①②符合．‎ 答案：B 6‎ ‎3．已知x>0，由不等式x＋≥2＝2，x＋＝＋＋≥3＝3，…我们可以得出推广结论：x＋≥n＋1(n∈N*)，则a＝________.‎ 解析：由观察可得：x＋＝＋≥(n＋1)·＝(n＋1)·＝n＋1，则a＝nn.‎ 答案：nn ‎4．已知经过计算和验证有下列正确的不等式：＋<2，＋<2，＋<2，根据以上不等式的规律，请写出一个对正实数m，n都成立的条件不等式________．‎ 解析：观察所给不等式可以发现：不等式左边两个根式的被开方数的和等于20，不等式的右边都是2，因此对正实数m，n都成立的条件不等式是：若m，n∈R＋，则当m＋n＝20时，有＋<2.‎ 答案：若m，n∈R＋，则当m＋n＝20时，有＋<2 ‎5．观察下列等式：‎ ‎①sin210°＋cos240°＋sin 10°cos 40°＝；‎ ‎②sin26°＋cos236°＋sin 6°cos 36°＝.‎ 由上面两题的结构规律，你能否提出一个猜想？‎ 并证明你的猜想．‎ 解析：由①②知，两角相差30°，运算结果为，‎ 猜想：sin2α＋cos2(α＋30°)＋sin αcos(α＋30°)＝.‎ 证明：左边＝＋＋‎ sin αcos(α＋30°)‎ ‎＝1－＋＋‎ sin α ‎＝1－cos 2α＋cos 2α－sin 2α＋sin 2α－＝＝右边 故sin2α＋cos2(α＋30°)＋sin αcos(α＋30°)＝.‎ ‎6．已知椭圆具有以下性质：若M、N是椭圆C上关于原点对称的两个点，点P 6‎ 是椭圆上任意一点，若直线PM、PN的斜率都存在，并记为kPM、kPN，那么kPM与kPN之积是与点P的位置无关的定值．试对双曲线－＝1写出具有类似的性质，并加以证明．‎ 解析：类似的性质为：若M、N是双曲线－＝1上关于原点对称的两个点，点P是双曲线上任意一点，若 直线PM、PN的斜率都存在，并记为kPM、kPN，那么kPM与kPN之积是与点P的位置无关的定值．‎ 证明如下：设点M、P的坐标为(m，n)、(x，y)，则 N(－m，－n)．‎ ‎∵点M(m，n)在已知双曲线上，‎ ‎∴n2＝m2－b2.同理y2＝x2－b2.‎ 则kPM·kPN＝·＝＝·＝(定值).‎ 6‎