2020高中数学 第1章 点、直线、面的位置关系6 线面垂直的判定和性质学案 苏教版必修2 4页

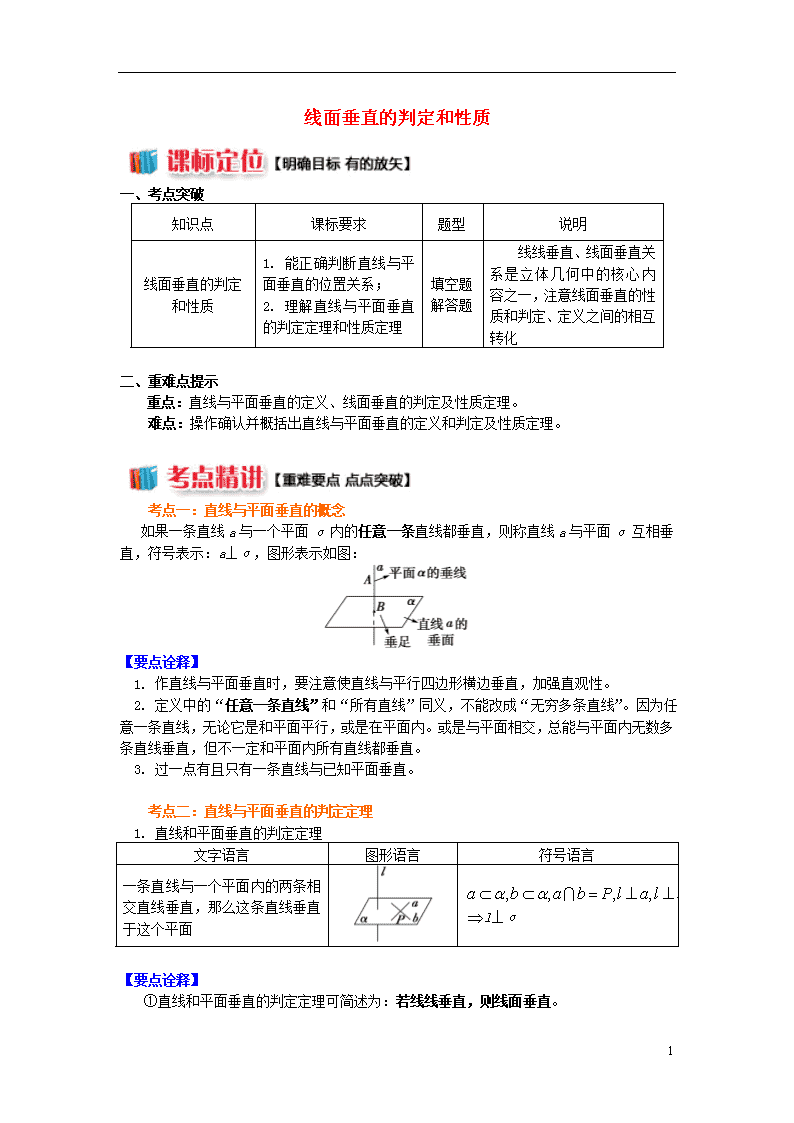
线面垂直的判定和性质 一、考点突破 知识点 课标要求 题型 说明 线面垂直的判定和性质 ‎1. 能正确判断直线与平面垂直的位置关系；‎ ‎2. 理解直线与平面垂直的判定定理和性质定理 填空题 解答题 线线垂直、线面垂直关系是立体几何中的核心内容之一，注意线面垂直的性质和判定、定义之间的相互转化 二、重难点提示 重点：直线与平面垂直的定义、线面垂直的判定及性质定理。‎ 难点：操作确认并概括出直线与平面垂直的定义和判定及性质定理。‎ 考点一：直线与平面垂直的概念 如果一条直线a与一个平面α内的任意一条直线都垂直，则称直线a与平面α互相垂直，符号表示：a⊥α，图形表示如图：‎ ‎【要点诠释】‎ ‎1. 作直线与平面垂直时，要注意使直线与平行四边形横边垂直，加强直观性。‎ ‎2. 定义中的“任意一条直线”和“所有直线”同义，不能改成“无穷多条直线”。因为任意一条直线，无论它是和平面平行，或是在平面内。或是与平面相交，总能与平面内无数多条直线垂直，但不一定和平面内所有直线都垂直。‎ ‎3. 过一点有且只有一条直线与已知平面垂直。‎ 考点二：直线与平面垂直的判定定理 ‎1. 直线和平面垂直的判定定理 文字语言 图形语言 符号语言 一条直线与一个平面内的两条相交直线垂直，那么这条直线垂直于这个平面 l⊥α ‎【要点诠释】‎ ‎①直线和平面垂直的判定定理可简述为：若线线垂直，则线面垂直。‎ 4‎ ‎②定理中的关键词语是“两条相交直线”。‎ ‎2. 推论：如果在两条平行直线中，有一条垂直于一个平面，那么另一条直线也垂直这个平面。‎ ‎【规律总结】判定线面垂直的方法 ‎（1）线面垂直的定义：a与α内任何直线都垂直a⊥α；‎ ‎（2）判定定理：l⊥α；‎ ‎（3）推论：a∥b，a⊥αb⊥α；‎ 考点三：直线与平面垂直的性质定理 ‎1. 直线和平面垂直的性质定理 文字语言 图形语言 符号语言 如果两条直线垂直于同一个平面，那么这两条直线平行 ‎⇒a∥b ‎2. 直线和平面垂直的性质 ‎①直线垂直于平面，则垂直于平面内任意直线；‎ ‎②垂直于同一个平面的两条直线平行。‎ ‎【核心突破】‎ ‎1. 线面垂直的定义具有双重性，既可以由线面垂直得出线线垂直，又可以由线线垂直得出线面垂直。‎ ‎2. 转化思想：垂直关系的转化 在解决直线与平面垂直的问题过程中，要注意直线与平面垂直定义、判定定理和性质定理的联合交替使用，即注意线线垂直和线面垂直的互相转化。‎ ‎3. 线面垂直的性质定理揭示了空间中“平行”与“垂直”关系的内在联系，提供了“垂直”与“平行”关系相互转化的依据。‎ 例题1 （直线和平面垂直的定义）‎ 下面叙述中：‎ ‎①若直线垂直于平面内的两条直线，则这条直线与平面垂直；②若直线与平面内的任意一条直线都垂直，则这条直线与平面垂直；③若直线垂直于梯形的两腰所在的直线，则这条直线垂直于两底边所在的直线；④若直线垂直于梯形的两底边所在的直线，则这条直线垂直于两腰所在的直线，其中正确的有（　　）‎ A. 1个　　　 B. 2个　　　 C. 3个　　　 D. 4个 思路分析：与线面垂直的定义及线面垂直的判定定理进行对照，区分异同，分析条件变换的影响，辨析正误。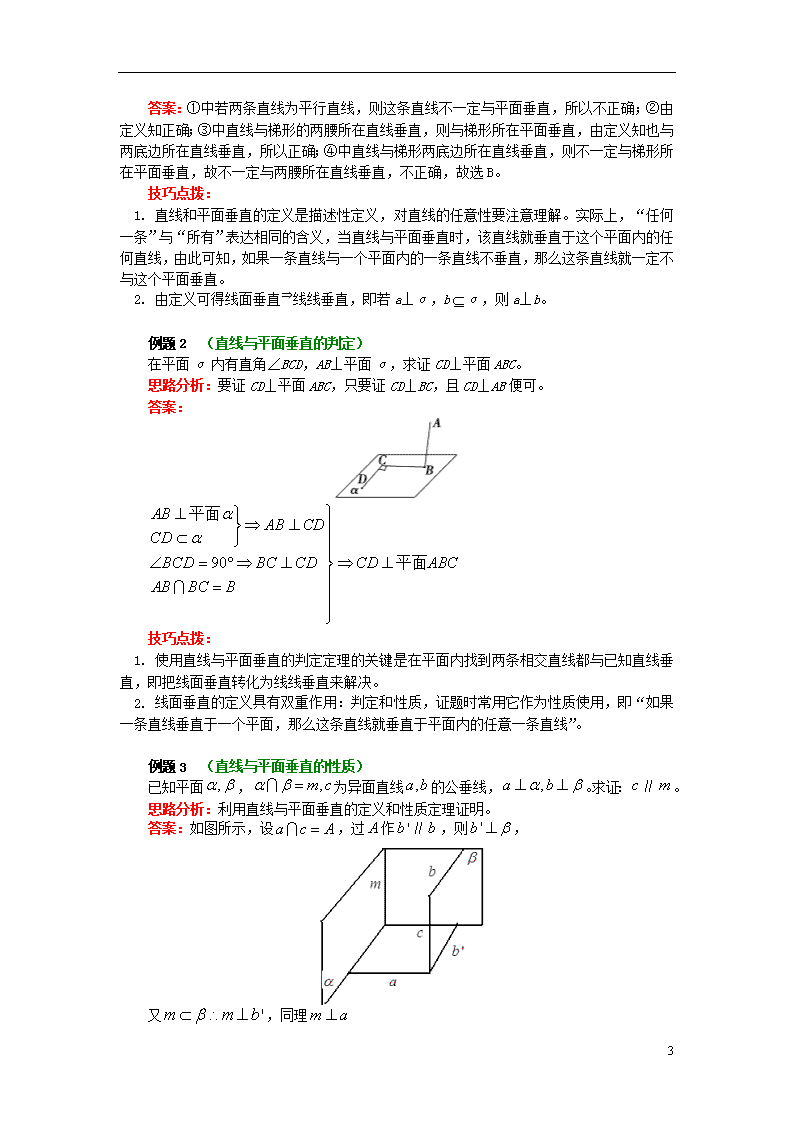‎ 4‎ 答案：①中若两条直线为平行直线，则这条直线不一定与平面垂直，所以不正确；②由定义知正确；③中直线与梯形的两腰所在直线垂直，则与梯形所在平面垂直，由定义知也与两底边所在直线垂直，所以正确；④中直线与梯形两底边所在直线垂直，则不一定与梯形所在平面垂直，故不一定与两腰所在直线垂直，不正确，故选B。‎ 技巧点拨：‎ ‎1. 直线和平面垂直的定义是描述性定义，对直线的任意性要注意理解。实际上，“任何一条”与“所有”表达相同的含义，当直线与平面垂直时，该直线就垂直于这个平面内的任何直线，由此可知，如果一条直线与一个平面内的一条直线不垂直，那么这条直线就一定不与这个平面垂直。‎ ‎2. 由定义可得线面垂直⇒线线垂直，即若a⊥α，bα，则a⊥b。‎ 例题2 （直线与平面垂直的判定）‎ 在平面α内有直角∠BCD，AB⊥平面α，求证CD⊥平面ABC。‎ 思路分析：要证CD⊥平面ABC，只要证CD⊥BC，且CD⊥AB便可。‎ 答案：‎ 技巧点拨：‎ ‎1. 使用直线与平面垂直的判定定理的关键是在平面内找到两条相交直线都与已知直线垂直，即把线面垂直转化为线线垂直来解决。‎ ‎2. 线面垂直的定义具有双重作用：判定和性质，证题时常用它作为性质使用，即“如果一条直线垂直于一个平面，那么这条直线就垂直于平面内的任意一条直线”。‎ 例题3 （直线与平面垂直的性质）‎ 已知平面，为异面直线的公垂线，。求证：∥。‎ 思路分析：利用直线与平面垂直的定义和性质定理证明。‎ 答案：如图所示，设，过作∥，则，‎ 又，同理 4‎ ‎，若与确定平面，则 ‎∥‎ 又 ‎∥。‎ 技巧点拨：直线与平面垂直的性质定理是平行关系和垂直关系的完美结合，利用垂直关系可判定平行，反过来，由平行关系，也可判定垂直关系，即两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面。‎ 立体几何中的翻折问题 ‎【满分训练】（浙江）已知矩形ABCD，AB＝1，BC＝，将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中（　　） ‎ A. 存在某个位置，使得直线AC与直线BD垂直 B. 存在某个位置，使得直线AB与直线CD垂直 C. 存在某个位置，使得直线AD与直线BC垂直 D. 对任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直 思路分析：关键是找出图形在翻折过程中变化的量与不变的量。‎ 答案：‎ 对于选项A，过点A作AE⊥BD，垂足为E，过点C作CF⊥BD，垂足为F，‎ 在图（1）中，由边AB，BC不相等可知点E，F不重合，‎ 在图（2）中，连接CE，若直线AC与直线BD垂直，‎ 又∵AC∩AE＝A，∴BD⊥面ACE，‎ ‎∴BD⊥CE，与点E，F不重合相矛盾，故A错误；‎ 对于选项B，若AB⊥CD，‎ 又∵AB⊥AD，AD∩CD＝D，‎ ‎∴AB⊥面ADC，‎ ‎∴AB⊥AC，由ABAB，‎ ‎∴不存在这样的直角三角形，∴C错误。‎ 由上可知D错误，故选B。‎ 技巧点拨：对于翻折问题，关键是找到题目中哪些关系改变，哪些关系没有改变。‎ 4‎