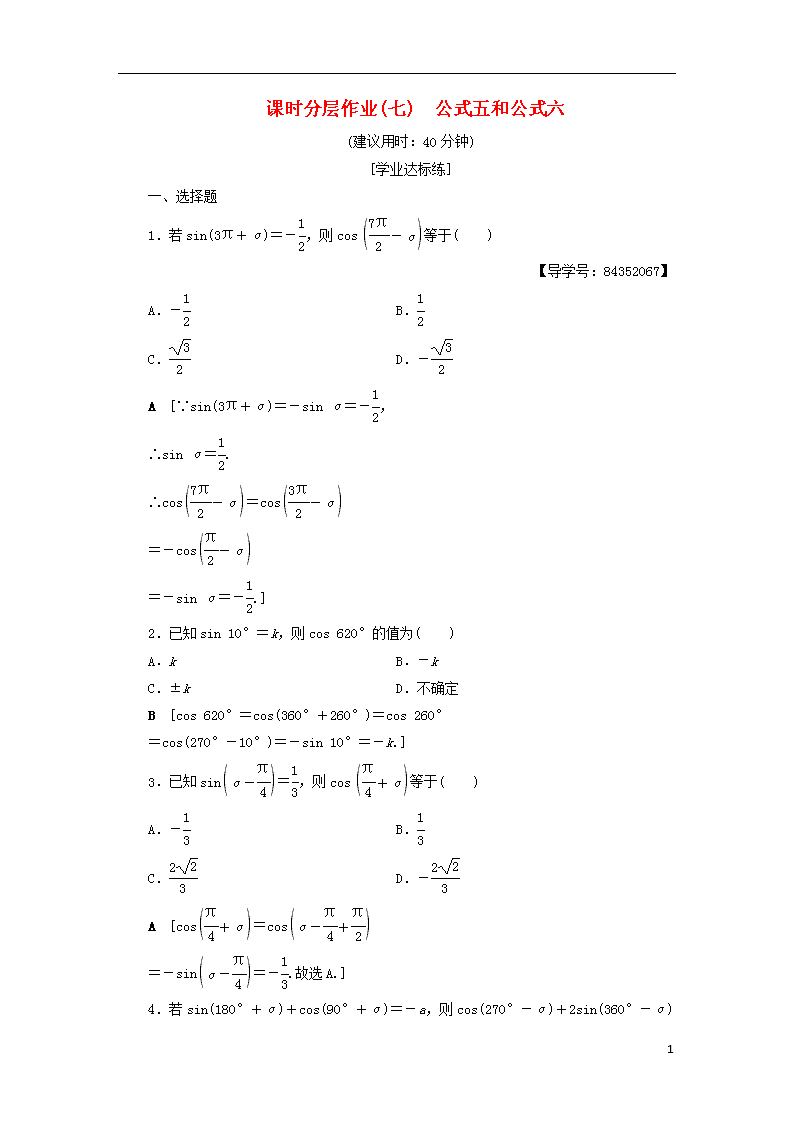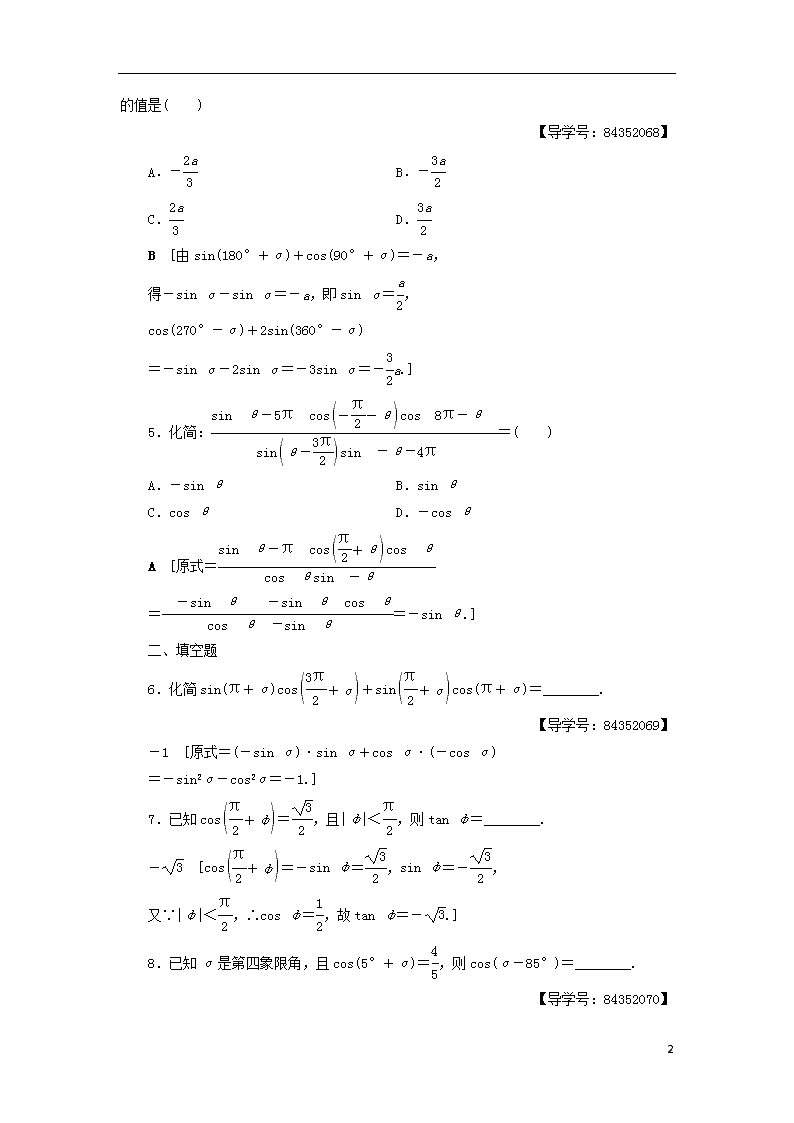- 63.00 KB
- 2021-06-23 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
课时分层作业(七) 公式五和公式六
(建议用时:40分钟)
[学业达标练]
一、选择题
1.若sin(3π+α)=-,则cos等于( )
【导学号:84352067】
A.- B.
C. D.-
A [∵sin(3π+α)=-sin α=-,
∴sin α=.
∴cos=cos
=-cos
=-sin α=-.]
2.已知sin 10°=k,则cos 620°的值为( )
A.k B.-k
C.±k D.不确定
B [cos 620°=cos(360°+260°)=cos 260°
=cos(270°-10°)=-sin 10°=-k.]
3.已知sin=,则cos等于( )
A.- B.
C. D.-
A [cos=cos
=-sin=-.故选A.]
4.若sin(180°+α)+cos(90°+α)=-a,则cos(270°-α)+2sin(360°-α)的值是( )
5
【导学号:84352068】
A.- B.-
C. D.
B [由sin(180°+α)+cos(90°+α)=-a,
得-sin α-sin α=-a,即sin α=,
cos(270°-α)+2sin(360°-α)
=-sin α-2sin α=-3sin α=-a.]
5.化简:=( )
A.-sin θ B.sin θ
C.cos θ D.-cos θ
A [原式=
==-sin θ.]
二、填空题
6.化简sin(π+α)cos+sincos(π+α)=________.
【导学号:84352069】
-1 [原式=(-sin α)·sin α+cos α·(-cos α)
=-sin2α-cos2α=-1.]
7.已知cos=,且|φ|<,则tan φ=________.
- [cos=-sin φ=,sin φ=-,
又∵|φ|<,∴cos φ=,故tan φ=-.]
8.已知α是第四象限角,且cos(5°+α)=,则cos(α-85°)=________.
【导学号:84352070】
- [因为α是第四象限角,且cos(5°+α)=>0,所以5°+α是第四象限角,
5
所以sin(5°+α)=-=-,
所以cos(α-85°)=cos(5°+α-90°)
=sin(5°+α)=-.]
三、解答题
9.已知角α的终边经过点P.
(1)求sin α的值;
(2)求的值.
【导学号:84352071】
[解] (1)因为点P,
所以|OP|=1,sin α=-.
(2)
==,
由三角函数定义知cos α=,故所求式子的值为.
10.求证:=.
[证明] 左边=
=
=,
右边=
==
5
==,
所以等式成立.
[冲A挑战练]
1.若f(cos x)=cos 2x,则f(sin 15°)的值为( )
A.- B.
C.- D.
A [因为f(sin 15°)=f(cos 75°)=cos 150°=-.]
2.计算sin21°+sin22°+sin23°+…+sin289°=( )
A.89 B.90
C. D.45
C [原式=(sin21°+sin289°)+(sin22°+sin288°)+…+(sin244°+sin246°)+sin245°=44+=.]
3.已知=2,则sin(θ-5π)sin=________.
【导学号:84352072】
[∵=2, sin θ=3cos θ,
∴tan θ=3.
sin(θ-5π)sin=sin θcos θ
=
==.]
4.已知锐角α终边上一点P的坐标是(2sin 2,-2cos 2),则α等于_______.
2- [cos α=
=sin 2,
5
∵α为锐角,∴α=2-.]
5.已知f(α)=.
(1)化简f(α);
(2)若f=-,且α是第二象限角,求tan α. 【导学号:84352073】
[解] (1)f(α)=
==sin α.
(2)由sin=-,得cos α=-,
又α是第二象限角,所以sin α==,
则tan α==-.
5
相关文档
- 高中数学必修5:2_5等比数列前n项和(2021-06-233页
- 2020版高中数学 第二章 数列数列的2021-06-233页
- 高中数学必修1教案:第九章直线平面2021-06-234页
- 江苏省常州一中、泰兴中学、南菁高2021-06-239页
- 2020高中数学 第2章 平面向量 第三2021-06-233页
- 2020高中数学第三章指数函数和对数2021-06-237页
- 高中数学选修第2章2_2_2同步训练及2021-06-234页
- 高中数学:新人教A版选修1-1 3_1变化2021-06-237页
- 2019学年高中数学暑假作业 第一部2021-06-234页
- 2020高中数学 第三章 空间向量与立2021-06-232页