湖南省益阳市2021届高三9月调研考试数学试题 Word版含答案 14页

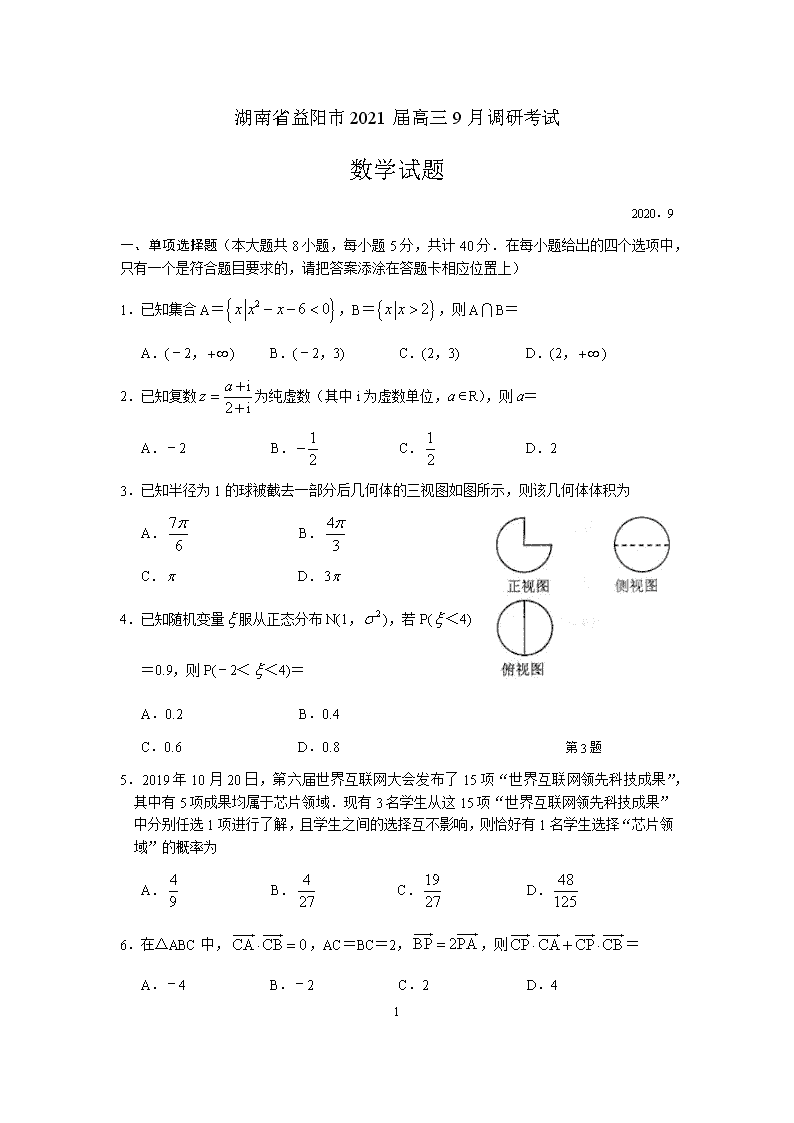
湖南省益阳市2021届高三9月调研考试 数学试题 ‎2020．9‎ 一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）‎ ‎1．已知集合A＝，B＝，则AB＝‎ ‎ A．(﹣2，) B．(﹣2，3) C．(2，3) D．(2，)‎ ‎2．已知复数为纯虚数（其中i为虚数单位，aR），则a＝‎ ‎ A．﹣2 B． C． D．2‎ ‎3．已知半径为1的球被截去一部分后几何体的三视图如图所示，则该几何体体积为 ‎ A． B．‎ C． D．‎ ‎4．已知随机变量服从正态分布N(1，)，若P(＜4)‎ ‎＝0.9，则P(﹣2＜＜4)＝‎ ‎ A．0.2 B．0.4‎ C．0.6 D．0.8 第3题 ‎5．2019年10月20日，第六届世界互联网大会发布了15项“世界互联网领先科技成果”，其中有5项成果均属于芯片领域．现有3名学生从这15项“世界互联网领先科技成果”中分别任选1项进行了解，且学生之间的选择互不影响，则恰好有1名学生选择“芯片领域”的概率为 ‎ A． B． C． D．‎ ‎6．在△ABC中，，AC＝BC＝2，，则＝‎ ‎ A．﹣4 B．﹣2 C．2 D．4‎ 14‎ ‎7．过抛物线C：x2＝2py(p＞0)的焦点F的直线交C于A，B两点，且，O为坐标原点，则＝‎ ‎ A． B． C．4 D．‎ ‎8．已知函数，若，则a的取值范围是 ‎ A．[﹣2，0] B．(，2]‎ ‎ C．[﹣2，2] D．(，﹣2][2，)‎ 二、 多项选择题（本大题共4小题，每小题5分， 共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）‎ ‎9．已知双曲线C：过点(3，)，则下列结论正确的是 A．C的焦距为4 B．C的离心率为 C．C的渐近线方程为 D．直线2x﹣y﹣1＝0与C有两个公共点 ‎10．已知定义在R上的偶函数在[0，1]上单调递增，且，则下列结论正确的是 A．直线x＝3是的一条对称轴 B．是周期为2的周期函数 C．在(1，2)上单调递减 D．x＝2是函数的一个零点 ‎11．下面的结论中，正确的是 ‎ A．若aR，则 ‎ B．若a＞0，b＞0，，则a＋b≥2‎ ‎ C．若b＞a＞0，m＞0，则 14‎ ‎ D．若a＞b＞0且，则ab＝1‎ ‎12．函数的部分图像如图中实线所示，图中的M、N是圆C与图像的两个交点，其中M在y轴上，C是图像与x轴的交点，则下列说法中正确的是 ‎ A．函数的一个周期为 ‎ B．函数的图像关于点(，0)成中心对称 ‎ C．函数在(，)上单调递增 ‎ D．圆C的面积为 ‎ 第12题 三、填空题（本大题共4小题， 每小题5分，共计20分．请把答案填写在答题卡相应位置上）‎ ‎13．若，则＝ ．‎ ‎14．的展开式中x的系数是 ．（用数字填写答案）‎ ‎15．已知函数，则的 零点个数为 ．‎ ‎16．已知正方体ABCD—A1B1C1D1的棱长为4，P是AA1中点，‎ 过点D1作平面，满足CP⊥平面，则平面与正方体 ABCD—A1B1C1D1的截面周长为 ．‎ ‎ 第16题 四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分10分）‎ 14‎ 在①，②，③这三个 条件中任选一个，补充在下面问题中，并完成问题的解答．‎ 问题：已知数列是等比数列，且，其中，，成等差数列．‎ ‎（1）求数列的通项公式；‎ ‎（2）记 ，求数列的前2n项和．‎ 注：如果选择多个条件分别解答，按第一个解答计分．‎ ‎18．（本小题满分12分）‎ 已知△ABC的角A，B，C对边分别为a，b，c，a＋acosC＝csinA，c＝．‎ ‎（1）求∠C；‎ ‎（2）求△ABC面积的最大值．‎ ‎19．（本小题满分12分）‎ 如图，四棱锥P—ABCD的底面为正方形，平面PAD⊥平面ABCD，PA＝PD．‎ ‎（1）求证：PD⊥AB；‎ ‎（2）若直线PA与BC所成角为，求平面PAD与平面PBC所成锐二面角的余弦值．‎ ‎20．（本小题满分12分）‎ 14‎ 已知6名某疾病病毒密切接触者中有1名感染病毒，其余5名未感染，需要通过化验血液来确定感染者．血液化验结果呈阳性的即为感染者，呈阴性即为未感染者．‎ ‎（1）若从这6名密切接触者中随机抽取2名，求抽到感染者的概率；‎ ‎（2）血液化验确定感染者的方法有：方法一是逐一化验；方法二是平均分组混合化验，先将血液样本平均分成若干组，对组内血液混合化验，若化验结果呈阴性，则该组血液不含病毒，若化验结果呈阳性，则对该组的备份血液逐一化验，直至确定感染者．‎ ‎（i）采取逐一化验，求所需化验次数的分布列及数学期望；‎ ‎（ii）采取平均分成三组混合化验（每组血液份数相同），求该分组方法所需化验次数的数学期望．‎ 你认为选择哪种化验方案更合理？请说明理由．‎ ‎21．（本小题满分12分）‎ 已知椭圆C：(a＞b＞0)的离心率为，且经过点A(，)．‎ ‎（1）求椭圆C的方程；‎ ‎（2）若不过坐标原点的直线l与椭圆C相交于M，N两点，且满足，求△MON面积最大时直线l的方程．‎ ‎22．（本小题满分12分）‎ 14‎ 已知函数，aR．‎ ‎（1）当a＝0时，求的单调区间；‎ ‎（2）当a＝1时，有成立，求实数m的取值范围．‎ 14‎ 14‎ 14‎ 14‎ 14‎ 14‎ 14‎ 14‎ 14‎