高中数学第一章解三角形1-2-3三角形中的几何计算课时作业含解析新人教A版必修5 6页

课时作业6　三角形中的几何计算 时间：45分钟 ‎——基础巩固类——‎ 一、选择题 ‎1．在△ABC中，A满足sinA＋cosA＝1，AB＝2，BC＝2，则△ABC的面积为(　A　)‎ A. B．2 C．3 D．6‎ 解析：由得 ‎∴A＝120°.由正弦定理，得＝，‎ ‎∴sinC＝.∴C＝30°，∴B＝30°，‎ ‎∴S△ABC＝AB·BCsinB＝×2×2×sin30°＝.‎ ‎2．在△ABC中，A＝60°，AB＝2，且△ABC的面积S△ABC＝，则边BC的长为(　A　)‎ A. B．3‎ C. D．7‎ 解析：∵S△ABC＝AB·ACsinA＝，∴AC＝1.‎ 由余弦定理可得BC2＝AB2＋AC2－2AB·ACcosA ‎＝4＋1－2×2×1×cos60°＝3，‎ 即BC＝.‎ ‎3．在△ABC中，a＝，b＝1，B＝30°，则△ABC的面积S为(　D　)‎ A. B. C.或 D.或 解析：由正弦定理＝，‎ 得sinA＝＝＝，‎ 所以A＝60°或A＝120°.‎ 当A＝60°时，C＝90°，S＝＝＝；‎ 当A＝120°时，C＝30°，‎ 6‎ S＝absinC＝××1×sin30°＝.‎ ‎4．在△ABC中，a，b，c分别为角A，B，C的对边，如果2b＝a＋c，B＝30°，△ABC的面积为，则b等于(　A　)‎ A．1＋ B. C. D．2＋ 解析：由acsin30°＝，得ac＝6，由余弦定理，得b2＝a2＋c2－2accos30°＝(a＋c)2－2ac－ac＝4b2－12－6，得b＝＋1.‎ ‎5．在△ABC中，AC＝，BC＝2，B＝60°，则BC边上的高等于(　B　)‎ A. B. C. D. 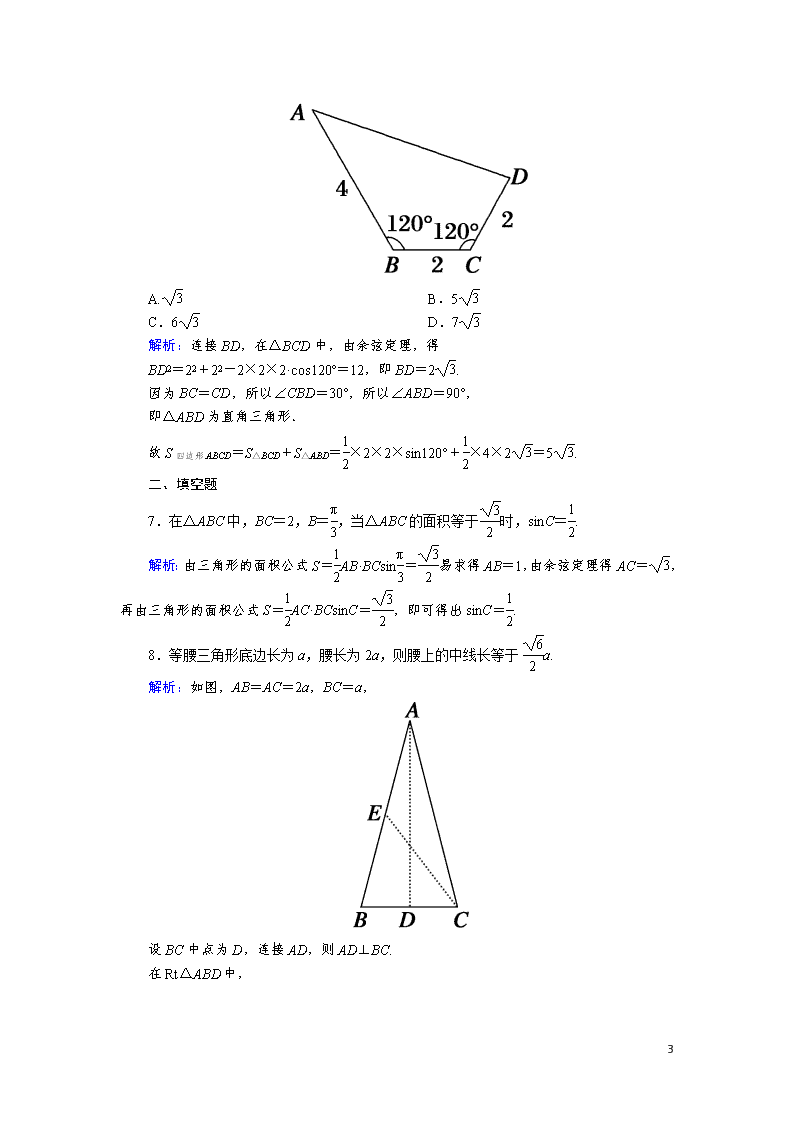解析：如图，在△ABC中，由余弦定理可知：‎ AC2＝AB2＋BC2－2AB·BCcosB，‎ 即7＝AB2＋4－2×2×AB×.‎ 整理得AB2－2AB－3＝0.‎ 解得AB＝－1(舍去)或AB＝3.‎ 故BC边上的高AD＝AB·sinB＝3sin60°＝.‎ ‎6．如图，在四边形ABCD中，已知B＝C＝120°，AB＝4，BC＝CD＝2，则该四边形的面积等于(　B　)‎ 6‎ A. B．5 C．6 D．7 解析：连接BD，在△BCD中，由余弦定理，得 BD2＝22＋22－2×2×2·cos120°＝12，即BD＝2.‎ 因为BC＝CD，所以∠CBD＝30°，所以∠ABD＝90°，‎ 即△ABD为直角三角形．‎ 故S四边形ABCD＝S△BCD＋S△ABD＝×2×2×sin120°＋×4×2＝5.‎ 二、填空题 ‎7．在△ABC中，BC＝2，B＝，当△ABC的面积等于时，sinC＝.‎ 解析：由三角形的面积公式S＝AB·BCsin＝易求得AB＝1，由余弦定理得AC＝，再由三角形的面积公式S＝AC·BCsinC＝，即可得出sinC＝.‎ ‎8．等腰三角形底边长为a，腰长为2a，则腰上的中线长等于a.‎ 解析：如图，AB＝AC＝2a，BC＝a，‎ 设BC中点为D，连接AD，则AD⊥BC.‎ 在Rt△ABD中，‎ 6‎ cosB＝＝＝.‎ 设AB中点为点E，连接CE，‎ 则在△BEC中，BE＝BC＝a，‎ 由余弦定理CE2＝CB2＋BE2－2CB·BE·cosB ‎＝a2＋a2－2a2·＝2a2－a2＝a2.‎ 所以CE＝a.‎ ‎9．在△ABC中，已知·＝tanA，当A＝时，△ABC的面积为.‎ 解析：因为·＝||·||cosA＝tanA，且A＝，所以||·||＝，所以△ABC的面积S＝||·||sinA＝××sin＝.‎ 三、解答题 ‎10．已知a，b，c分别为锐角△ABC三个内角A，B，C的对边，2bsinC＝c.‎ ‎(1)求角B的大小；‎ ‎(2)若b＝2，△ABC的面积为，求a，c的值．‎ 解：(1)因为2bsinC＝c，‎ 所以根据正弦定理得2sinBsinC＝sinC，‎ 所以sinB＝，‎ 又因为B∈，所以B＝60°.‎ ‎(2)根据题意得 所以解得 ‎11．在△ABC中，若角A，B，C的对边分别是a，b，c，求证：‎ －＝－.‎ 证明：左边＝－ ‎＝－ ‎＝－－＋ ‎＝－－＋ ‎＝－＝右边，所以等式成立．‎ 6‎ ‎——能力提升类——‎ ‎12．△ABC的周长为20，面积为10，A＝60°，则BC的长等于(　C　)‎ A．5 B．6‎ C．7 D．8‎ 解析：如图，由题意得 由②得bc＝40.‎ 由③得a2＝b2＋c2－bc＝(b＋c)2－3bc ‎＝(20－a)2－3×40，‎ 所以a＝7.故选C.‎ ‎13．在△ABC中，a，b，c分别为内角A，B，C的对边．若△ABC的面积为，A＝15°，则＋的值为(　D　)‎ A. B．2 C．2 D. 解析：△ABC的面积S＝bcsinA＝，‎ 所以2bc＝.‎ 由余弦定理得cosA＝＝－＝－＝－sinA，‎ 所以＋＝＝2(sinA＋cosA)‎ ‎＝2sin(A＋45°)＝2sin60°＝.故选D.‎ ‎14．在△ABC中，D为边BC上一点，BD＝DC，∠ADB＝120°，AD＝2.若△ADC的面积为3－，则∠BAC＝60°.‎ 解析：设BD＝a，则DC＝2a，由已知条件有S△ADC＝AD·DC·sin∠ADC＝×2×2asin60°＝a＝3－，解得a＝－1，由余弦定理分别得到AB2＝6，AC2＝24－12 6‎ ‎，再由余弦定理得cos∠BAC＝，所以∠BAC＝60°.‎ ‎15．在△ABC中，角A，B，C所对的边分别为a，b，c，设S为△ABC的面积，满足S＝(a2＋b2－c2)．‎ ‎(1)求角C的大小；‎ ‎(2)求sinA＋sinB的最大值．‎ 解：(1)由题意可知absinC＝×2abcosC.‎ 所以tanC＝，‎ 因为0