高考数学复习 17-18版 第5章 第28课 函数建模问题(二)——三角函数、解三角形 16页

第28课 函数建模问题(二)——三角函数、解三角形 ‎[最新考纲]‎ 内容 要求 A B C 正(余)弦定理及其应用 ‎√‎ ‎1．仰角和俯角 在同一铅垂平面内的水平视线和目标视线的夹角，目标视线在水平视线上方时叫仰角，目标视线在水平视线下方时叫俯角．(如图①)．‎ ‎①　　　　　　　②‎ 图281‎ ‎2．方位角和方向角 ‎(1)方位角：从指北方向顺时针转到目标方向线的水平角，如B点的方位角为α(如图②)．‎ ‎(2)方向角：相对于某正方向的水平角，如南偏东30°等．‎ ‎1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎(1)从A处望B处的仰角为α，从B处望A处的俯角为β，则α，β的关系为α＋β＝180°.(　　)‎ ‎(2)俯角是铅垂线与视线所成的角，其范围为.(　　)‎ ‎(3)方位角与方向角其实质是一样的，均是确定观察点与目标点之间的位置关系．(　　)‎ ‎(4)如图282，为了测量隧道口AB的长度，可测量数据a，b，γ进行计算．(　　)‎ 图282‎ ‎[答案]　(1)×　(2)×　(3)√　(4)√‎ ‎2．(教材改编)如图283，已知A，B两点分别在河的两岸，某测量者在点A所在的河岸边另选定一点C，测得AC＝‎50 m，∠ACB＝45°，∠CAB＝105°，则A，B两点的距离为________m.‎ 图283‎ ‎50　[因为∠ACB＝45°，∠CAB＝105°，所以∠B＝30°.由正弦定理可知＝，即＝，解得AB＝‎50 m．]‎ ‎3．在‎200米高的山顶上，测得山下一塔顶与塔底的俯角分别为30°，60°，则塔高为________米．‎ 　[如图所示，山的高度MN＝‎200米，塔高为AB，CN＝MB＝，AC＝＝＝.所以塔高AB＝200－＝(米)．]‎ ‎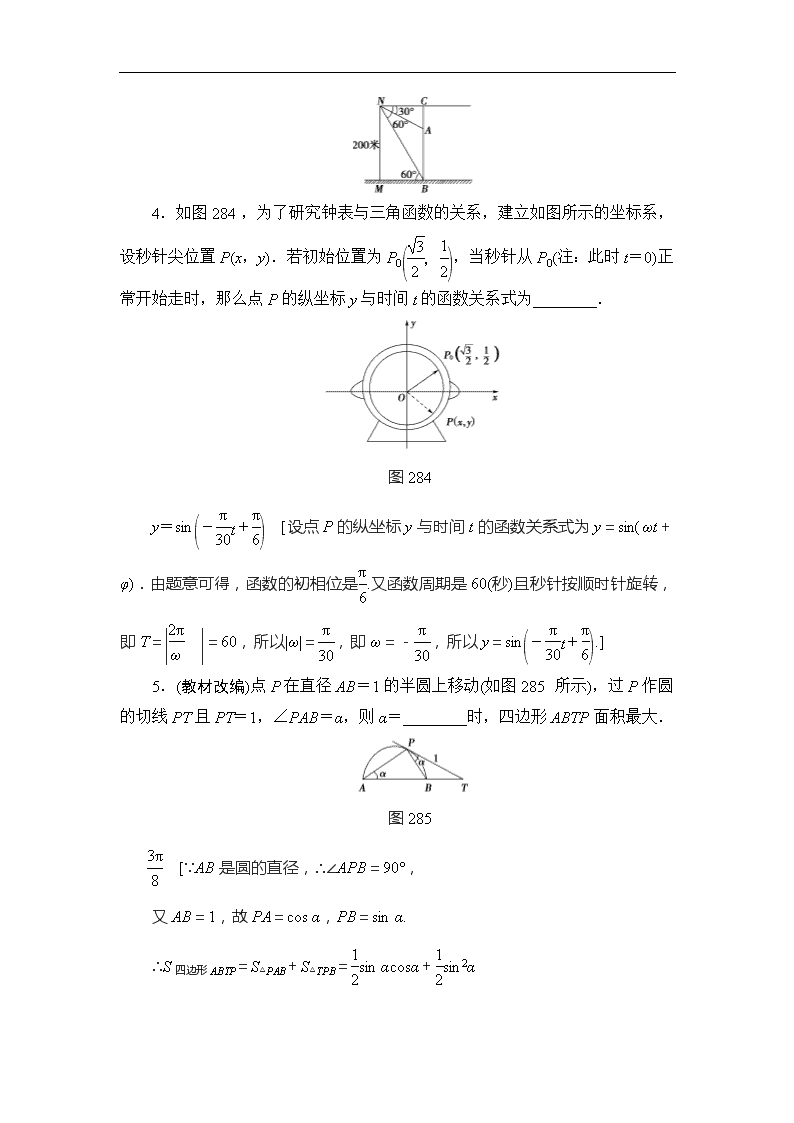4．如图284，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针尖位置P(x，y)．若初始位置为P0，当秒针从P0(注：此时t＝0)正常开始走时，那么点P的纵坐标y与时间t的函数关系式为________．‎ 图284‎ y＝sin　[设点P的纵坐标y与时间t的函数关系式为y＝sin(ωt＋φ)．由题意可得，函数的初相位是.又函数周期是60(秒)且秒针按顺时针旋转，即T＝＝60，所以|ω|＝，即ω＝－，所以y＝sin.]‎ ‎5．(教材改编)点P在直径AB＝1的半圆上移动(如图285所示)，过P作圆的切线PT且PT＝1，∠PAB＝α，则α＝________时，四边形ABTP面积最大．‎ 图285‎ 　[∵AB是圆的直径，∴∠APB＝90°，‎ 又AB＝1，故PA＝cos α，PB＝sin α.‎ ‎∴S四边形ABTP＝S△PAB＋S△TPB＝sin αcosα＋sin2α ‎＝sin 2α＋ ‎＝sin＋.‎ ‎∵α∈，－<2α－<，‎ ‎∴当2α－＝，即α＝时 S四边形ABTP最大．]‎ 测量问题 角度1　测量距离 ‎　如图286，A，B两点在河的同侧，且A，B两点均不可到达，要测出AB的距离，测量者可以在河岸边选定两点C，D，若测得CD＝ km，∠ADB＝∠CDB＝30°，∠ACD＝60°，∠ACB＝45°，求A，B两点间的距离．‎ 图286‎ ‎[解]　在△ADC中，CD＝，∠ACD＝60°，∠ADC＝30°＋30°＝60°，‎ ‎∴△ADC为正三角形，即AC＝CD＝.‎ 在△BDC中，∠DBC＝180°－30°－45°－60°＝45°.‎ 由正弦定理得，‎ ＝，‎ ‎∴BC＝＝.‎ 在△ABC中，由余弦定理得 AB2＝＋－2×××＝，‎ ‎∴AB＝(km)．‎ 所以A，B的距离为km.‎ 角度2　测量高度 ‎　如图287，一辆汽车在一条水平的公路上向正西行驶，到A处时测得公路北侧一山顶D在西偏北30°的方向上，行驶‎600 m后到达B处，测得此山顶在西偏北75°的方向上，仰角为30°，则此山的高度CD＝______m.‎ 图287‎ ‎100　[由题意，在△ABC中，∠BAC＝30°，∠ABC＝180°－75°＝105°，故∠ACB＝45°.‎ 又AB＝600 m，故由正弦定理得＝，解得BC＝300 m.‎ 在Rt△BCD中，CD＝BC·tan 30°＝300× ‎＝100(m)．]‎ 角度3　测量角度 ‎　在海岸A处，发现北偏东45°方向、距离A处(－1)海里的B处有一艘走私船；在A处北偏西75°方向、距离A处2海里的C处的缉私船奉命以10海里/小时的速度追截走私船．同时，走私船正以10海里/小时的速度从B处向北偏东30°方向逃窜，问缉私船沿什么方向能最快追上走私船？最少要花多长时间？ 【导学号：62172152】‎ ‎[解]　设缉私船t小时后在D处追上走私船，则有CD＝10t，BD＝10t.‎ 在△ABC中，AB＝－1，AC＝2，∠BAC＝120°.‎ 根据余弦定理，可得 BC＝ ‎＝，‎ 由正弦定理，得sin∠ABC＝sin∠BAC＝×＝，∴∠ABC＝45°，因此BC与正北方向垂直．‎ 于是∠CBD＝120°.在△BCD中，由正弦定理，得 sin∠BCD＝＝＝，‎ ‎∴∠BCD＝30°，又＝，‎ 即＝，得t＝.∴当缉私船沿北偏东60°的方向能最快追上走私船，最少要花小时．‎ ‎[规律方法]　1.研究测量距离(高度)问题，解决此问题的方法是：选择合适的辅助测量点，构造三角形，将问题转化为求某个三角形的边长问题，从而利用正、余弦定理求解．‎ ‎2．测量角度问题应关注以下三点 ‎(1)测量角度时，首先应明确方位角及方向角的含义．‎ ‎(2)求角的大小时，先在三角形中求出其正弦或余弦值．‎ ‎(3)在解应用题时，要根据题意正确画出示意图，通过这一步可将实际问题转化为可用数学方法解决的问题，解题中也要注意体会正、余弦定理“联袂”使用的优点.‎ 方案设计的问题 ‎　(2017·苏州期中)如图288，在海岸线l一侧C处有一个美丽的小岛，某旅游公司为方便游客，在l上设立了A，B两个报名点，满足A，B，C中任意两点间的距离为‎10 km.公司拟按以下思路运作：先将A，B两处游客分别乘车集中到AB之间的中转点D处(点D异于A，B两点)，然后乘同一艘轮游轮前往C岛．据统计，每批游客A处需发车2辆，B处需发车4辆，每辆汽车每千米耗费2元，游轮每千米耗费12元．设∠CDA＝α，每批游客从各自报名点到C岛所需运输成本为S元．‎ 图288‎ ‎(1)写出S关于α的函数表达式，并指出α的取值范围；‎ ‎(2)问：中转点D距离A处多远时，S最小？ 【导学号：62172153】‎ ‎[解]　(1)由题知在△ACD中，∠CAD＝，∠CDA＝α，AC＝10，∠ACD＝－α.‎ 由正弦定理知＝＝，‎ 即CD＝，AD＝，‎ 所以 S＝4AD＋8BD＋12CD＝12CD－4AD＋80＝＋80‎ ‎＝20＋60.‎ ‎(2)S′＝20，‎ 令S′＝0得cos α＝.‎ 当cos α>时，S′<0；当cos α<时，S′>0，‎ 所以当cos α＝时，S取得最小值，‎ 此时sin α＝，AD＝＝5＋，‎ 所以中转点C距A处 km时，运输成本S最小．‎ ‎[规律方法]　此类问题常以正、余弦定理为解题切入点，通过引入参变量“α”建立关于三角函数的解析式，在此基础上，借助最值工具(如：三角函数的有界性、导数或基本不等式)求解函数最值，从而解决实际问题．‎ ‎[变式训练1]　如图289，两座建筑物AB，CD的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是‎9 m和‎15 m，从建筑物AB的顶部A 看建筑物CD的视角∠CAD＝45°.‎ 图289‎ ‎(1)求BC的长度；‎ ‎(2)在线段BC上取一点P(点P与点B，C不重合)，从点P看这两座建筑物的视角分别为∠APB＝α，∠DPC＝β，问点P在何处时，α＋β最小？‎ ‎[解]　(1)作AE⊥CD，垂足E，则CE＝9，DE＝6，设BC＝x，‎ 则tan∠CAD＝tan(∠CAE＋∠DAE)＝＝＝1，‎ 化简得x2－15x－54＝0，‎ 解得x＝18或x＝－3(舍)．‎ 所以，BC的长度为18 m.‎ ‎(2)设BP＝t，则CP＝18－t(00，f(t)是增函数，‎ 所以，当t＝15－27时，f(t)取得最小值，即tan(α＋β)取得最小值，‎ 因为－t2＋18t－135<0恒成立，所以f(t)<0，‎ 所以tan(α＋β)<0，α＋β∈，‎ 因为y＝tan x在上是增函数，所以当t＝15－27时，α＋β取得最小值．‎ 答：当BP为(15－27)m时，α＋β取得最小值.‎ 三角函数模型的简单应用 ‎　如图2810，一个水轮的半径为‎4 m，水轮圆心O距离水面‎2 m，已知水轮逆时针旋转且每分钟转动5圈．如果当水轮上点P从水中浮现时(图中点P0)开始计算时间．‎ 图2810‎ ‎(1)将点P距离水面的高度z m表示为时间t s的函数，求其解析式；‎ ‎(2)求点P第一次到达最高点时所需要的时间．‎ ‎[解]　(1)以水平方向为x轴，竖直方向为y轴，建立直角坐标系(图略)，设角φ是以Ox为始边，OP0为终边的角，OP每分钟内所转过的角为5×2π，OP每秒钟内所转过的角为＝，‎ 得z＝4sin＋2，‎ 当t＝0时，z＝0，得sin φ＝－，‎ 即φ＝－，故所求的函数关系式为z＝4sin＋2.‎ ‎(2)令z＝4sin＋2＝6，‎ 得sin＝1，‎ 所以t－＝，得t＝4，‎ 故点P第一次到达最高点大约需要4 s.‎ ‎[规律方法]　1.三角函数模型在实际中的应用体现在两个方面：一是用已知的模型去分析解决实际问题，二是把实际问题抽象转化成数学问题，建立三角函数模型解决问题，其关键是合理建模．‎ ‎2．建模的方法是认真审题，把问题提供的“条件”逐条地“翻译”成“数学语言”，这个过程就是数学建模的过程．‎ ‎[变式训练2]　某实验室一天的温度(单位：℃)随时间t(单位：h)的变化近似满足函数关系：f(t)＝10－cost－sint，t∈[0,24)．‎ ‎(1)求实验室这一天的最大温差；‎ ‎(2)若要求实验室温度不高于‎11 ℃‎，则在哪段时间实验室需要降温？‎ ‎[解]　(1)因为f(t)＝10－2 ‎＝10－2sin，‎ 又0≤t＜24，‎ 所以≤t＋＜，－1≤sin≤1.‎ 当t＝2时，sin＝1；‎ 当t＝14时，sin＝－1.‎ 于是f(t)在[0,24)上取得最大值12，取得最小值8.‎ 故实验室这一天最高温度为12 ℃，最低温度为8 ℃，最大温差为4 ℃.‎ ‎(2)依题意，当f(t)＞11时实验室需要降温．‎ 由(1)得f(t)＝10－2sin，‎ 故有10－2sin＞11，‎ 即sin＜－.‎ 又0≤t＜24，因此＜t＋＜，即10＜t＜18.‎ 故在10时至18时实验室需要降温．‎ ‎[思想与方法]‎ 解三角形应用题的两种情形 ‎(1)已知量与未知量全部集中在一个三角形中，可用正弦定理或余弦定理求解．‎ ‎(2)已知量与未知量涉及到两个或两个以上的三角形，这时需作出这些三角形，先解够条件的三角形，然后逐步求解其他三角形，有时需设出未知量，从几个三角形中列出方程(组)，解方程(组)得出所要求的解．‎ ‎[易错与防范]‎ ‎1．“方位角”与“方向角”的区别：方位角大小的范围是[0,2π)，方向角大小的范围一般是.‎ ‎2．在实际问题中，可能会遇到空间与平面(地面)同时研究的问题，这时最好画两个图形，一个空间图形，一个平面图形，这样处理起来既清楚又不容易出现错误．‎ 课时分层训练(二十八)‎ A组　基础达标 ‎(建议用时：30分钟)‎ ‎1．(2017·淮海中学模拟)如图2811，有一块半径为R的半圆形空地，开发商计划征地建一个矩形游泳池ABCD和其附属设施，附属设施占地形状是等腰△CDE，其中O为圆心，A，B在圆的直径上，C，D，E在圆周上．‎ 图2811‎ ‎(1)设∠BOC＝θ，征地面积记为f(θ)，求f(θ)的表达式；‎ ‎(2)当θ为何值时，征地面积最大？ 【导学号：62172154】‎ ‎[解]　(1)连结OE，OC，可得OE＝R，OB＝Rcos θ，BC＝Rsin θ；θ∈.‎ ‎∴f(θ)＝2S梯形OBCE＝R2(sin θcos θ＋cos θ)θ∈.‎ ‎(2)f′(θ)＝－R2(2sin θ－1)(sin θ＋1)．‎ 令f′(θ)＝0，‎ ‎∴sin θ＋1＝0(舍)或者sin θ＝.‎ ‎∵θ∈，‎ 当θ∈时， f′(θ)>0；当θ∈时，f′(θ)<0，‎ ‎∴当θ＝时，f(θ)取得最大值．‎ 答：θ＝时，征地面积最大．‎ ‎2. (2017·镇江期中)‎ 广告公司为某游乐场设计某项设施的宣传画，根据该设施的外观，设计成的平面图由半径为‎2m的扇形AOB和三角区域BCO构成，其中C，O，A在一条直线上，∠ACB＝，记该设施平面图的面积为S(x) m2，∠AOB＝x rad，其中＜x＜π.‎ 图2812‎ ‎(1)写出S(x)关于x的函数关系式；‎ ‎(2)如何设计∠AOB，使得S(x)有最大值？‎ ‎[解]　(1)由已知可得∠CBO＝x－，S扇形AOB＝lr＝2x，‎ 在△BCO中，由正弦定理可得：‎ ＝，所以CO＝2(sin x－cos x)，‎ 从而S△CBO＝BO·CO·sin∠BOC＝2sin2x－2sin xcos x，‎ 所以S(x)＝2sin2x－2sin xcos x＋2x＝2sin x(sin x－cos x)＋2x.‎ ‎ (2)S′(x)＝2(sin 2x－cos 2x)＋2＝2sin＋2，‎ 由S′(x)＝0，解得x＝，‎ 令S′(x)＞0，解得＜x＜，所以增区间是；‎ 令S′(x)＜0，解得＜x＜π，所以减区间是；‎ 所以S(x)在x＝处取得最大值是2＋ m2.‎ 答：设计成∠AOB＝时，该设施的平面图面积最大是2＋ m2.‎ B组　能力提升 ‎(建议用时：15分钟)‎ ‎1．(2017·无锡期中)如图2813，某自行车手从O点出发，沿折线O－A－B－O匀速骑行，其中点A位于点O南偏东45°且与点O相距20千米．该车手于上午8点整到达点A,8点20分骑至点C，其中点C位于点O南偏东(45°－α)(其中sin α＝，0°＜α＜90°)且与点O相距‎5千米(假设所有路面及观测点都在同一水平面上)．‎ 图2813‎ ‎(1)求该自行车手的骑行速度；‎ ‎(2)若点O正西方向27.5千米处有个气象观测站E，假定以点E为中心的3.5千米范围内有长时间的持续强降雨．试问：该自行车手会不会进入降雨区，并说明理由. 【导学号：62172155】‎ ‎[解]　(1)由题意知，OA＝20，OC＝5，∠AOC＝α，sin α＝.‎ 由于0°＜α＜90°，所以cos α＝＝.‎ 由余弦定理，得AC＝＝5.‎ 所以该自行车手的行驶速度为＝15(千米/小时)．‎ ‎(2)如图，设直线OE与AB相交于点M.在△AOC中，由余弦定理，得：‎ cos∠OAC＝＝＝，‎ 从而sin∠OAC＝＝＝.‎ 在△AOM中，由正弦定理，得：‎ OM＝＝＝20.‎ 由于OE＝27.5＞20＝OM，所以点M位于点O和点E之间，且ME＝OE－OM＝7.5.‎ 过点E作EH⊥AB于点H，则EH为点E到直线AB的距离. ‎ 在Rt△EHM中，‎ EH＝EM·sin∠EMH＝EM·sin∠EMH＝EM·sin(45°－∠OAC)＝7.5×＝＜3.5.‎ 所以该自行车手会进入降雨区．‎ ‎2．(2017·启东中学高三第一次月考)如图2814，某广场中间有一块边长为‎2百米的菱形状绿化区ABCD，其中BMN是半径为‎1百米的扇形，∠ABC＝.管理部门欲在该地从M到D修建小路：在弧MN上选一点P(异于M，N两点)，过点P修建与BC平行的小路PQ.问：点P选择在何处时，才能使得修建的小路与PQ及QD的总长最小？并说明理由．‎ 图2814‎ ‎[解]　连结BP，过P作PP1⊥BC垂足为P1，过Q作QQ1⊥BC垂足为Q1.‎ 设∠PBP1＝θ，＝－θ 若0<θ<，在Rt△PBP1中，PP1＝sin θ，BP1＝cos θ，‎ 若θ＝，则PP1＝sin θ，BP1＝cos θ，‎ 若<θ<，则PP1＝sin θ，BP1＝cos(π－θ)＝－cos θ，‎ ‎∴PQ＝2－cos θ－sin θ.‎ 在Rt△QBQ1中，‎ QQ1＝PP1＝sin θ，CQ1＝sin θ，CQ＝sin θ，‎ DQ＝2－sin θ.‎ 所以总路径长 f(θ)＝－θ＋4－cos θ－sin θ，‎ f′(θ)＝sin θ－cos θ－1＝2sin－1‎ 令f′(θ)＝0，得θ＝.‎ 当0<θ<时，f′(θ)<0，‎ 当<θ<时，f′(θ)>0.‎ 所以当θ＝时，总路径最短．‎ 答：当BP⊥BC时，总路径最短．‎