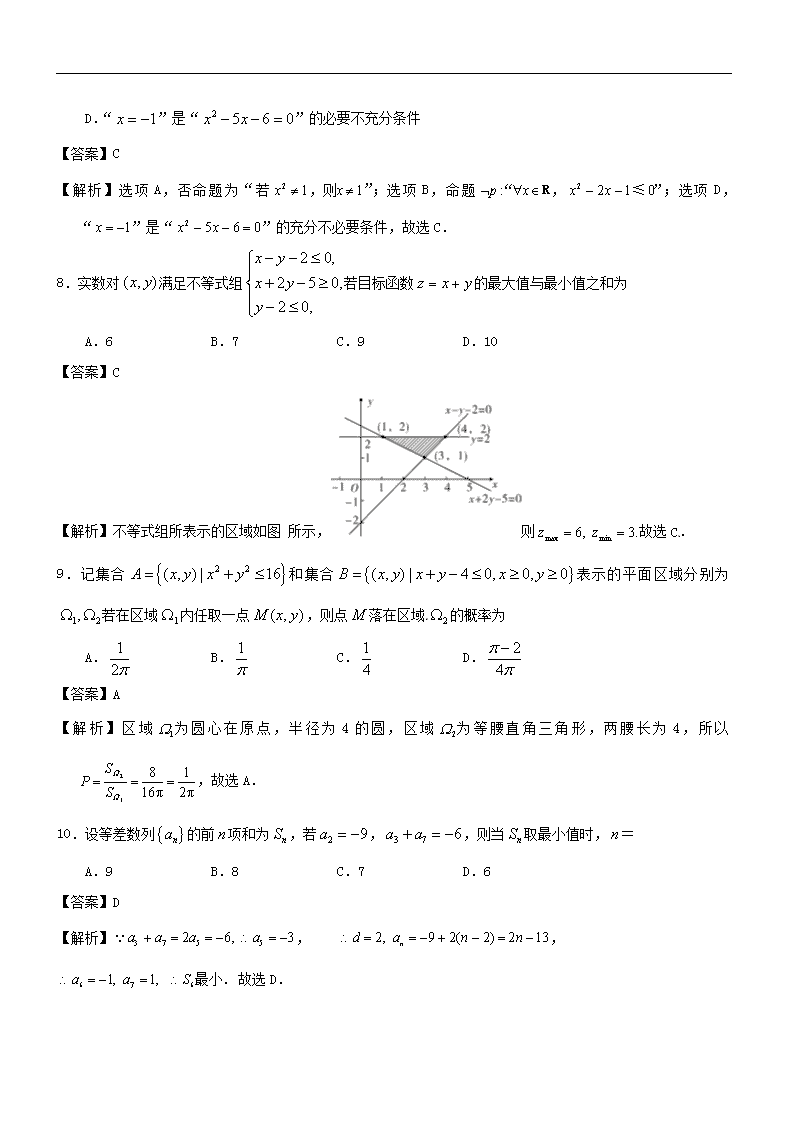2014届高三数学二轮双基掌握《选择填空题》（新题+典题）10 6页

‎2014届高三数学二轮双基掌握《选择填空题》（新题+典题）10(含详解)‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．设集合，，则＝‎ A． B． C． D．‎ ‎【答案】B ‎【解析】当时，；当时，；当时，，．故选B．‎ ‎2．在复平面内，复数对应的点位于 A．第四象限 B．第三象限 C．第二象限 D．第一象限 ‎【答案】A ‎【解析】A.‎ ‎3．已知，，若，则＝‎ A．4 B．3 C．2 D．1‎ ‎【答案】B ‎【解析】因为，所以，即，即，所以，故选B．‎ ‎4．一个几何体的三视图如图1所示，其中正视图是一个正三角形，则该几何体的体积为正视图 ‎1 1‎ ‎1 ‎ 侧视图 俯视图 A．1 B． C． D．‎ ‎【答案】B ‎【解析】由三视图可知，此几何体为三棱锥，如图 ，其中正视图为，是边长为2的正三角形，，且，底面为等腰直角三角形，，所以体积为，故选B．‎ ‎5．执行如图2所示的程序框图，则输出的的值是 A．8 B．6 C．4 D．3‎ ‎【答案】A ‎【解析】‎ ‎；.故选A．‎ ‎6．下列函数中既不是奇函数也不是偶函数的是 A． B．‎ C． D．‎ ‎【答案】D ‎【解析】根据奇偶性定义知，A、B为偶函数，C为奇函数，D定义域为不关于原点对称，故选D．‎ ‎7．下列说法正确的是 A．命题“若，则”的否命题为：“若，则”‎ B．若命题，则命题 C．命题“若，则”的逆否命题为真命题 D．“”是“”的必要不充分条件 ‎【答案】C ‎【解析】选项A，否命题为“若”；选项B，命题R，；选项D，“”是“”的充分不必要条件，故选C．‎ ‎8．实数对满足不等式组若目标函数的最大值与最小值之和为 A．6 B．7 C．9 D．10‎ ‎【答案】C ‎【解析】不等式组所表示的区域如图 所示，则故选C．‎ ‎9．记集合和集合表示的平面区域分别为若在区域内任取一点，则点落在区域的概率为 A． B． C． D．‎ ‎【答案】A ‎【解析】区域为圆心在原点，半径为4的圆，区域为等腰直角三角形，两腰长为4，所以，故选A．‎ ‎10．设等差数列的前项和为，若，，则当取最小值时，＝‎ A．9 B．8 C．7 D．6‎ ‎【答案】D ‎【解析】， ，‎ ‎. 故选D．‎ ‎11．对于函数，则下列说法正确的是 A．该函数的值域是 ‎ B．当且仅当时， ‎ C．当且仅当时，该函数取得最大值1‎ D．该函数是以为最小正周期的周期函数 ‎【答案】B ‎【解析】由图象知，函数值域为，A错；当且仅当时，该函数取得最大值，C错；最小正周期为，D错．故选B．‎ ‎12．已知为上的可导函数，且，均有，则有 A．，‎ B．，‎ C．，‎ D．，‎ ‎【答案】D ‎【解析】构造函数则，‎ 因为均有并且，所以，故函数在R上单调递减，所以，‎ 即 也就是，故选D．‎ 二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．‎ ‎13．某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果分成五组：第一组，第二组，……，第五组 ‎．图3是按上述分组方法得到的频率分布直方图，若成绩大于或等于14秒且小于16秒认为良好，则该班在这次百米测试中成绩良好的人数等于 ．‎‎0.38‎ 频率 组距 ‎0.32‎ ‎0.16‎ ‎0.08‎ ‎0.06‎ 秒 ‎13 14 15 16 17 18‎ ‎【答案】27‎ ‎【解析】．‎ ‎14．在锐角△中，角、、所对的边分别为、、，若，且，则△的面积为 ．‎ ‎【答案】‎ ‎【解析】，‎ ‎，‎ ‎，又是锐角三角形 ‎，‎ ‎．‎ ‎15．正三棱锥内接于球，且底面边长为，侧棱长为2，则球的表面积为 ．‎ ‎【答案】‎ ‎【解析】如图，设三棱锥的外接球球心为O，半径为r，BC=CD=BD=，‎ AB=AC=AD=2，，M为正的中心，则DM=1，AM=，OA=OD=r，所以，解得，所以．‎ ‎16．如图4，椭圆的中心在坐标原点，为左焦点，、分别为长轴和短轴上的一个顶点，当时，此类椭圆称为“黄金椭圆”．类比“黄金椭圆”，可推出“黄金双曲线”的离心率为 ．‎ ‎【答案】‎ ‎【解析】由图知，，整理得，即，解得，故．‎