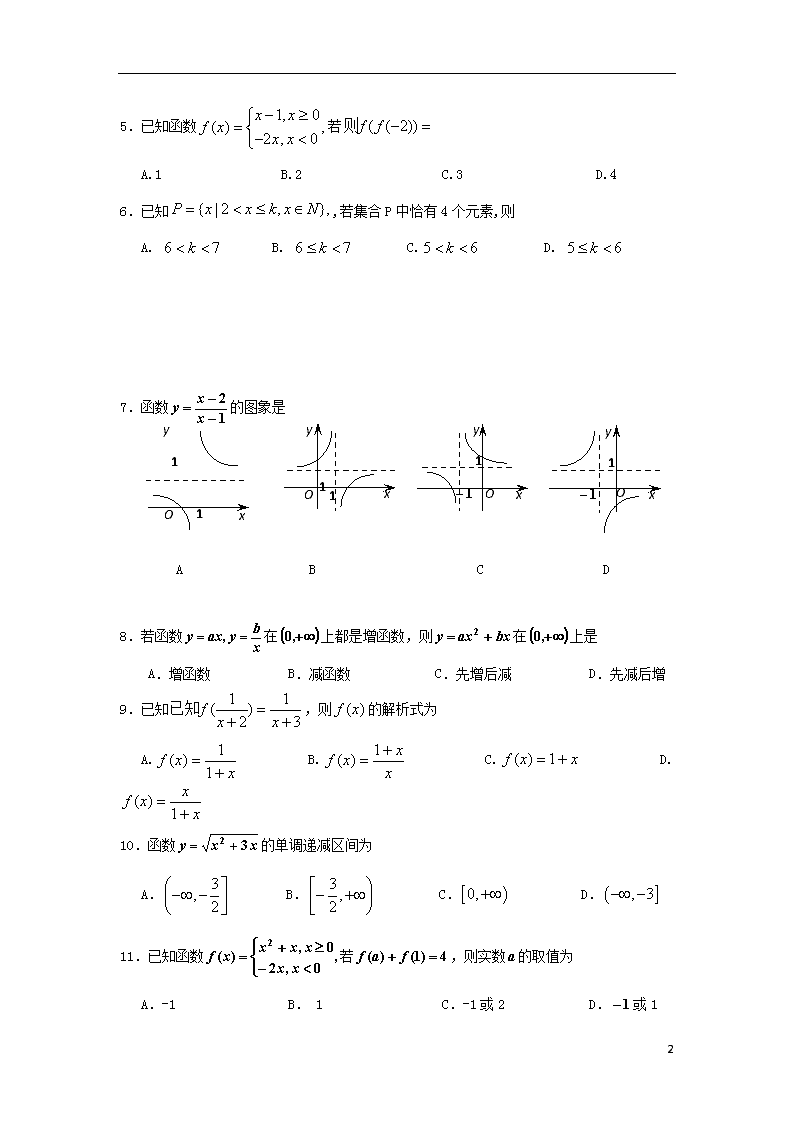2020学年高一数学上学期开学考试试题 新人教版新版 8页

‎2019高一上学期开学考试卷 数 学 注意：1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分。考试时间： 120 分钟 。答卷前，考生务必将自己的姓名和考号填写或填涂在答题卷指定的位置，将条形码张贴在指定位置 ‎2、选择题答案用2B铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案；不能答在试题卷上。‎ ‎3、主观题必须用黑色字迹的钢笔或签字笔在答题卷上作答，答案必须写在答题卷各题目指定区域内的相应位置上，超出指定区域的答案无效；如需改动，先划掉原来的答案，然后再写上新的答案。‎ 第I卷（选择题，共60分）‎ 一、选择题（本大题共12小题，每小题5分，共60分，每小题只有一个正确答案）‎ ‎1.设全集则=‎ A. B． C． D．‎ ‎2．设集合，则下列关系中正确的是 A. B． C． D．‎ ‎3．下列图形能表示函数的图象的是 A B C D ‎4.若，则 A. B.或 C. D. ‎ 8‎ ‎5．已知函数若 ‎ A.1 B.2 C.3 D.4 ‎ ‎6．已知,若集合P中恰有4个元素,则 ‎ A. B. C. D. ‎ y O x y ‎1‎ O x y ‎1‎ O x y ‎1‎ ‎7．函数的图象是 ‎1‎ ‎1‎ x O ‎1‎ ‎ A B C D ‎ ‎ ‎8．若函数在上都是增函数，则在上是 ‎ A．增函数 B．减函数 C．先增后减 D．先减后增 ‎9．已知，则的解析式为 A. B. C. D.‎ ‎10．函数的单调递减区间为 A． B． C． D．‎ ‎11．已知函数若，则实数的取值为 ‎ A．-1 B． 1 C．-1或2 D．或1‎ 8‎ ‎12.设,都是的子集,如果叫做集合的长度,则集合M∩N的长度的最小值为 A. B. C. D. ‎ 第II卷（非选择题，共90分）‎ 二、填空题（本大题共4小题，每小题5分，共20分） ‎ ‎13．集合，用列举法表示为 .‎ ‎14．若方程的两根为，则= ．‎ ‎15. 若，则 .‎ ‎16. .‎ 三、解答题（本大题共6小题，共70分. 解答应写出文字说明、证明过程或演算步骤．）‎ ‎17．（本小题满分10分） ‎ 8‎ ‎19. （本小题满分12分）已知集合．‎ ‎（１）若，求实数的值；‎ ‎（2）若，求实数的取值范围．‎ ‎20. （本小题满分12分）‎ 8‎ ‎21．（本小题满分12分）已知函数．‎ ‎（1）判断函数在上的单调性并加以证明；‎ ‎（2）对任意的，若不等式恒成立，求实数的取值范围．‎ ‎22．（本小题满分12分）某农贸公司按每担200元的价格收购某农产品，并按每100元纳税10元（又称征税率为10个百分点）进行纳税，计划可收购万担，政府为了鼓励收购公司多收购这种农产品，决定将征税降低（）个百分点，预测收购量可增加个百分点.‎ 8‎ 桂林市第十八中学17级高一上学期开学考数学答案 一、 选择题答案 DBDCC BBDDD DB 二、 填空题答案 ‎ ‎ 三、 解答题答案 ‎ …………‎ ‎…………………………‎ ‎………………………………………………………………………………‎ ‎19．解：（1）…………………………………………………………………2分 所以有……………………………………………………………………5分 8‎ ‎（2）由得…………………………………………………………………8分 ‎………………………………………………………………11分 ‎…………………………12分 ‎20．………………………5分 ‎………………………………………………………7分 ‎……………………………9分 ‎…………………………11分 ‎…………………………………12分 ‎21．解：（I）在上单调递增．‎ 证明：设，则 ‎ ‎ ‎∵，∴，‎ ‎∴，即，∴在上单调递增．………………………‎ 8‎ ‎6分 ‎（II）由已知可得，‎ ‎∵，∴恒成立，‎ 即，‎ 由（1）知，‎ ‎∴，即．…………………………………………………………………………12分 ‎22．‎ ‎…………………………6分 ‎ ‎ ‎…………………………………………………………………………12分 8‎