2021高考数学一轮复习专练68高考大题专练八不等式证明选讲含解析理新人教版 4页

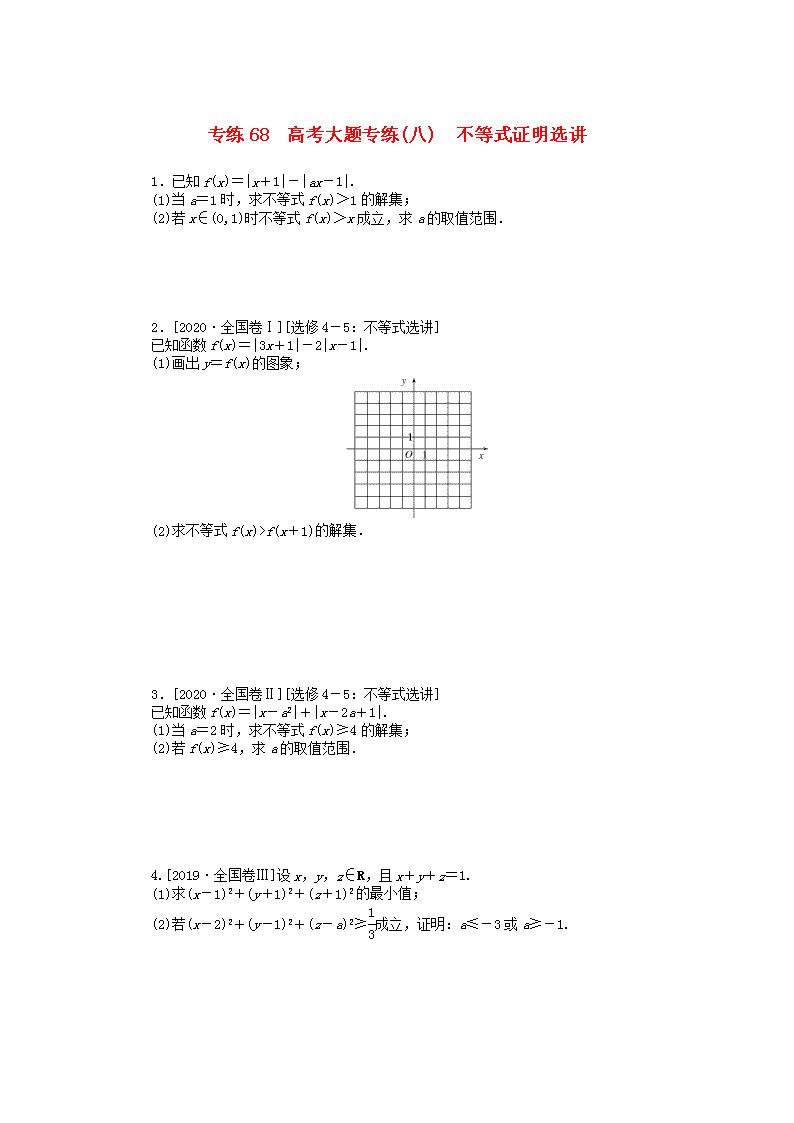
专练68　高考大题专练(八)　不等式证明选讲 ‎1．已知f(x)＝|x＋1|－|ax－1|.‎ ‎(1)当a＝1时，求不等式f(x)＞1的解集；‎ ‎(2)若x∈(0,1)时不等式f(x)＞x成立，求a的取值范围．‎ ‎2．[2020·全国卷Ⅰ][选修4－5：不等式选讲]‎ 已知函数f(x)＝|3x＋1|－2|x－1|.‎ ‎(1)画出y＝f(x)的图象；‎ ‎(2)求不等式f(x)>f(x＋1)的解集．‎ ‎3．[2020·全国卷Ⅱ][选修4－5：不等式选讲]‎ 已知函数f(x)＝|x－a2|＋|x－‎2a＋1|.‎ ‎(1)当a＝2时，求不等式f(x)≥4的解集；‎ ‎(2)若f(x)≥4，求a的取值范围．‎ ‎4.[2019·全国卷Ⅲ]设x，y，z∈R，且x＋y＋z＝1.‎ ‎(1)求(x－1)2＋(y＋1)2＋(z＋1)2的最小值；‎ ‎(2)若(x－2)2＋(y－1)2＋(z－a)2≥成立，证明：a≤－3或a≥－1.‎ ‎5．已知函数f(x)＝|2x＋1|－|x－4|.‎ ‎(1)解关于x的不等式f(x)>2；‎ ‎(2)若不等式f(x)≥ax＋－恒成立，求实数a的取值范围．‎ 专练68　高考大题专练(八)　不等式证明选讲 ‎1．解析：(1)当a＝1时，f(x)＝|x＋1|－|x－1|，‎ 即f(x)＝ 故不等式f(x)＞1的解集为.‎ ‎(2)当x∈(0,1)时|x＋1|－|ax－1|＞x成立等价于当x∈(0,1)时|ax－1|<1成立．‎ 若a≤0，则当x∈(0,1)时|ax－1|≥1；‎ 若a＞0，则|ax－1|＜1的解集为，‎ 所以≥1，故0＜a≤2.‎ 综上，a的取值范围为(0,2]．‎ ‎2．解析：(1)由题设知 f(x)＝ y＝f(x)的图象如图所示．‎ ‎(2)函数y＝f(x)的图象向左平移1个单位长度后得到函数y＝f(x＋1)的图象．‎ y＝f(x)的图象与y＝f(x＋1)的图象的交点坐标为.‎ 由图象可知当且仅当x<－时，y＝f(x)的图象在y＝f(x＋1)的图象上方．‎ 故不等式f(x)>f(x＋1)的解集为.‎ ‎3．解析：(1)当a＝2时，f(x)＝ 因此，不等式f(x)≥4的解集为.‎ ‎(2)因为f(x)＝|x－a2|＋|x－‎2a＋1|≥|a2－‎2a＋1|＝(a－1)2，故当(a－1)2≥4，即|a－1|≥2时，f(x)≥4.所以当a≥3或a≤－1时，f(x)≥4.‎ 当－12，得x>－3，则x≥4；‎ 当－2，得x>，则2，得x<－7，则x<－7.‎ 综上，不等式f(x)>2的解集为.‎ ‎(2)因为f(x)＝画出函数y＝f(x)的图象，如图所示，‎ 令y＝ax＋－，则y＋＝a的图象过定点P.由于函数y＝f(x)的最小值为－，不等式f(x)≥ax＋－恒成立，所以y＝ax＋－的图象恒在y＝f(x)的图象的下方，所以－1≤a≤1.‎