高考数学专题复习（精选精讲）练习7-立体几何(理)习题精选精讲 19页

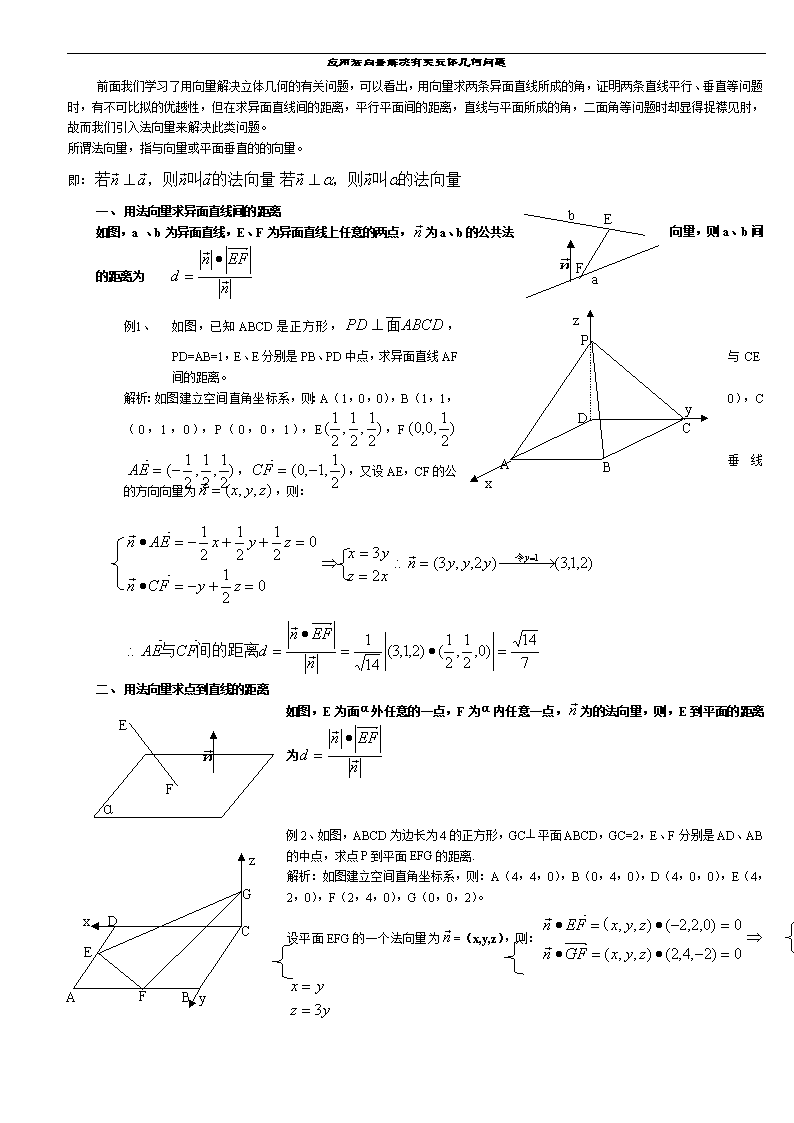
应用法向量解决有关立体几何问题 前面我们学习了用向量解决立体几何的有关问题，可以看出，用向量求两条异面直线所成的角，证明两条直线平行、垂直等问题时，有不可比拟的优越性，但在求异面直线间的距离，平行平面间的距离，直线与平面所成的角，二面角等问题时却显得捉襟见肘，故而我们引入法向量来解决此类问题。‎ 所谓法向量，指与向量或平面垂直的的向量。‎ 即：‎ a b F E 一、 用法向量求异面直线间的距离 如图，a 、b为异面直线，E、F为异面直线上任意的两点，为a、b的公共法向量，则a、b间的距离为 ‎ A P D C B y z x 例1、 如图，已知ABCD是正方形，，PD=AB=1，E、E分别是PB、PD中点，求异面直线AF与CE间的距离。‎ 解析：如图建立空间直角坐标系，则：A（1，0，0），B（1，1，0），C（0，1，0），P（0，0，1），E，F ，，又设AE，CF的公垂线的方向向量为，则：‎ ‎ ‎ 二、 用法向量求点到直线的距离 E F α 如图，E为面α外任意的一点，F为α内任意一点，为的法向量，则，E到平面的距离为 例2、如图，ABCD为边长为4的正方形，GC⊥平面ABCD，GC=2，E、F分别是AD、AB的中点，求点PB A C D E F G y z x 到平面EFG的距离.‎ 解析：如图建立空间直角坐标系，则：A（4，4，0），B（0，4，0），D（4，0，0），E（4，2，0），F（2，4，0），G（0，0，2）。‎ 设平面EFG的一个法向量为=（x,y,z），则： ‎ ‎（直线与平面的距离及平面与平面间的距离类同与点到平面的距离，请读者自己验证，这里不再赘述）‎ 一、 用法向量求直线与平面所成的角 E F α ‎ 如图，直线EF交平面α于F，为的一个法向量，则直线EF与平面α所成的角为 例3、如图，长方体ABCD-A1B1C1D1中，，E、F分别是AB，C1D1的中点，求：（1）、A1B1与面A1EF所成的角。（2）、B C1到面A1EF的距离 。‎ z x y 解：如图建立空间直角坐标系，则，A（，0，0），C（0，，0），B（，，0），C1（0，，0），D1（0，0，1），A1（，0，1），E（，，0），F（0，，1）。（1）、设平面A1EF的一个法向量为=（x,y,z），则：，故，因此，A1B1与面A1EF所成的角为。‎ 用向量法研究立体几何问题 ‎1.1、用传统方法解决立体几何问题与用向量法解决立体几何问题之比较 用传统方法解决立体几何问题，通常都必须添加辅助线，并且要经过各种手段进行转化，它具有较大的灵活性，学生掌握起来比较困难。空间向量的引入，给传统的立体几何内容注入了新的活力，向量是既有大小又有方向的量，既具有图形的直观性，又有代数推理的严密性，是数形结合的一个很好的桥梁。而空间向量是处理空间问题的重要方法，通过将空间元素间的位置关系转化为数量关系，将过去的形式逻辑证明转化为数值计算，化繁难为简易，化复杂为简单，为学生处理某些立体几何问题提供了的新视角。借助空间向量这一工具，可以降低思维难度，增加了可操作性，从而减轻了学生负担，使他们对立体几何更容易产生兴趣。下面举例说明：‎ ‎ 例 如图，在正方体ABCD－A1B‎1C1D中，E、F F A1‎ B1‎ C1‎ D1‎ B C D A E Ｇ Ｈ 分别是BB1、CD的中点. ‎ ‎(I)求AE与D‎1F所成的角 ‎(II)证明面AED⊥面A1FD1‎ 解: (I)取AB中点G,连结AG,FG.‎ 因为F是CD的中点,所以GF、AD平行且相等,‎ 又A1D1、AD平行且相等,所以GF、A1D1平行且相等,‎ 故GFD1A1是平行四边形,AG∥D1F. ‎ 设A1G与AE相交于点H,‎ 则∠AHA1是AE与D1F所成的角,‎ 因为E是BB1的中点,‎ 所以Rt△A1AG≌Rt△ABE, ∠GA1A=∠GAH，从而∠AHA1=90°,‎ 即直线AE与D1F所成角为直角.  ‎ ‎    (II)　　∵AC1是正方体,         　∴AD⊥面DC1.‎ ‎         又D‎1F面DC1,          　∴AD⊥D‎1F,‎ 由(I)知AE⊥D1F,‎ 又AD∩AE=A,‎ 所以D1F⊥面AED.‎ 又因为D1F面A1FD1,     ‎ 所以 面AED⊥面A1FD1.  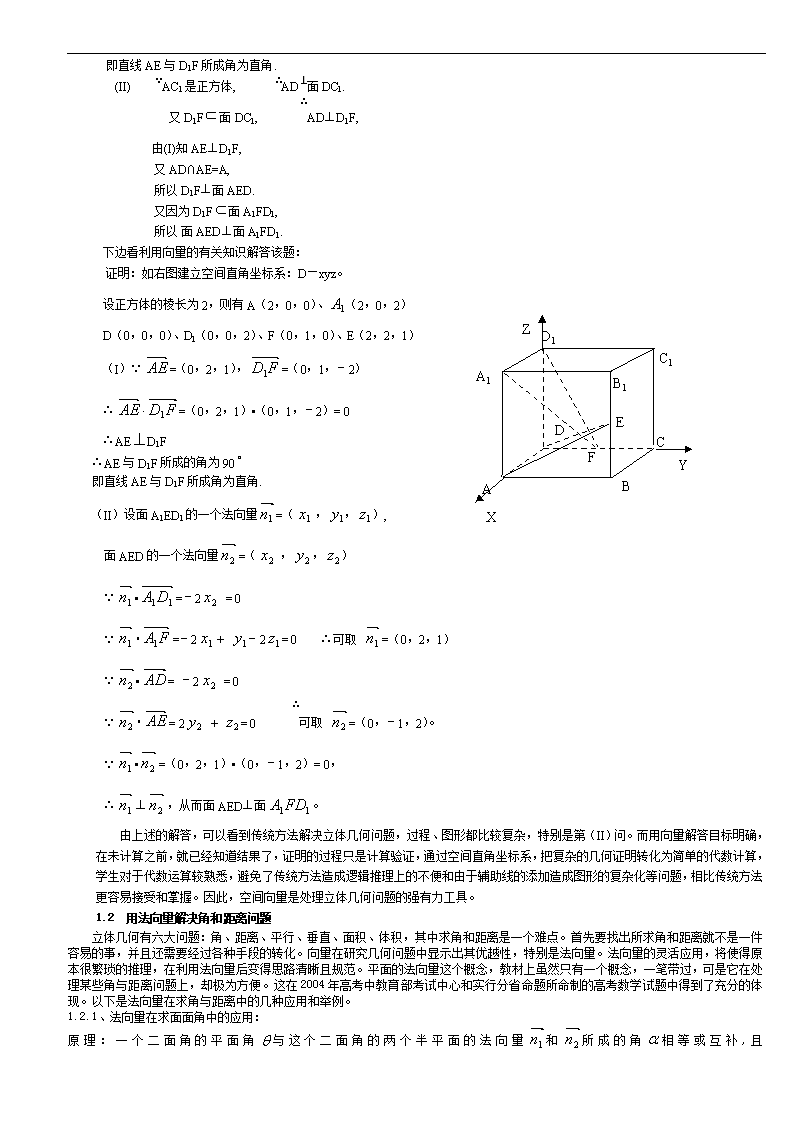‎ 下边看利用向量的有关知识解答该题：‎ ‎ 证明：如右图建立空间直角坐标系：D—xyz。‎ F A1‎ B1‎ C1‎ D1‎ B C D A E Y X Z 设正方体的棱长为2，则有A（2，0，0）、（2，0，2）‎ D（0，0，0）、D1（0，0，2）、F（0，1，0）、E（2，2，1）‎ ‎（I）∵=（0，2，1），=（0，1，－2）‎ ‎∴=（0，2，1）•（0，1，－2）= 0‎ ‎∴AED1F ‎∴AE与D1F所成的角为90‎ 即直线AE与D1F所成角为直角.   ‎ ‎（II）设面A1ED1的一个法向量=（ ，，）,‎ 面AED的一个法向量=（ ，，）‎ ‎∵•=－2 = 0‎ ‎    ∵•=－2 + －2= 0        ∴可取 =（0，2，1）‎ ‎∵•= －2 = 0        ‎ ‎∵•= 2 + = 0            ∴可取 =（0，－1，2）。‎ ‎∵•=（0，2，1）•（0，－1，2）= 0，‎ ‎∴⊥，从而面AED⊥面。‎ 由上述的解答，可以看到传统方法解决立体几何问题，过程、图形都比较复杂，特别是第（II）问。而用向量解答目标明确，在未计算之前，就已经知道结果了，证明的过程只是计算验证，通过空间直角坐标系，把复杂的几何证明转化为简单的代数计算，学生对于代数运算较熟悉，避免了传统方法造成逻辑推理上的不便和由于辅助线的添加造成图形的复杂化等问题，相比传统方法更容易接受和掌握。因此，空间向量是处理立体几何问题的强有力工具。‎ ‎1.2 用法向量解决角和距离问题 立体几何有六大问题：角、距离、平行、垂直、面积、体积，其中求角和距离是一个难点。首先要找出所求角和距离就不是一件容易的事，并且还需要经过各种手段的转化。向量在研究几何问题中显示出其优越性，特别是法向量。法向量的灵活应用，将使得原本很繁琐的推理，在利用法向量后变得思路清晰且规范。平面的法向量这个概念，教材上虽然只有一个概念，一笔带过，可是它在处理某些角与距离问题上，却极为方便。这在2004年高考中教育部考试中心和实行分省命题所命制的高考数学试题中得到了充分的体现。以下是法向量在求角与距离中的几种应用和举例。‎ ‎1.2.1‎‎、法向量在求面面角中的应用：‎ 原理：一个二面角的平面角与这个二面角的两个半平面的法向量和所成的角相等或互补,且 ‎。‎ 例1、（2004全国高考）如图，直三棱柱ABC—A1B1C1中，∠ACB=90°，AC=1，CB=，侧棱AA1=1，侧面AA1B1B的两条对角线交点为D，B1C1的中点为M.‎ ‎（Ⅰ）求证：CD⊥平面BDM；‎ D C A A B C B M Y X Z ‎（Ⅱ）求面B1BD与面CBD所成二面角的大小. ‎ D C A A B C B M 解析：如右图，以C为原点建立空间直角坐标系.‎ ‎（Ⅰ）B（，0，0），B1（，1，0），A1（0，1，1）, C1（0，1，0）‎ D，M（，1，0），‎ 则 ∴CD⊥BD，CD⊥DM.‎ 因为BD、DM为平面BDM内两条相交直线，‎ 所以CD⊥平面BDM.‎ ‎（Ⅱ）设BD中点为G，连结B1G，则 ‎ G， ,‎ ‎∴，‎ ‎∴，又CDBD ‎∴的夹角等于所求的二面角的平面角 所以所求的二面角等于 ‎1.2.2‎法向量在求线面角中的应用：‎ 原理：设平面的斜线L与平面所的角为，与斜线L同方向的向量和平面的法向量所成角，则与互余或与的补角互余，且。‎ 下面举例说明：‎ 例 已知正方体ABCD—A1B1C1D1中，E是AB的中点，求直线AE与平面ABCD所成角的大小。‎ Y A1‎ A B1‎ C1‎ D1‎ B C D Z X E 解析：如图，以D为原点建立空间直角坐标系，设正方体的棱长为2，则 ‎ A（2，0，0），E（2，1，2），B（2，2，0），C（0，2，2）‎ ‎ =（0，2，0），=（-2，0，2）‎ ‎ ∵•=2y = 0 ‎ ‎∵•= －2x +2Z = 0‎ ‎∴可取=（1，0，1）‎ ‎∴‎ ‎∴直线AE与平面ABCD所成角的大小为 ‎1.2.3‎‎、法向量在求异面直线间的距离中应用：‎ 原理：设分别以这两异面直线上任意两点为起点和终点的向量为，与这两条异面直线都垂直的向量为（即和两异面直线都平行的平面的法向量），则两异面直线间的距离是在方向上的正射影向量的模，即d=。‎ 下面举例说明：‎ 例 已知正方体ABCD—A1B1C1D1的棱长为1，求直线DA与AC的距离。‎ 分析：此题是课本习题（高二下（B）P50页），学生解答有困难，主要原因是不知如何作出那段距离，用向量法，建立空间直角坐标系，可避免作辅助线，大大降低了难度。‎ A1‎ A B1‎ C1‎ D1‎ B C D Y Z X 解析：如图，建立空间直角坐标系，则 A（1，0，0），A（1，0，1），C（0，1，0），D（0，0，0）‎ ‎=（0，0，1），=（1，0，1），=（-1，1，0）‎ 设=（x,y,z）是和这两条异面直线都垂直的一个向量 ‎∵•= x +y = 0‎ ‎∵•=－x +y = 0 ‎ ‎∴可取=（1，1，－1）‎ ‎∴‎ ‎1.2.4‎‎、法向量在求点到平面的距离中的应用：‎ 原理：设分别以平面外一点P与平面内一点M（平面内异于垂足的任一点）为起点和终点的向量为，平面的法向量为，则P到平面的距离d等于在方向上正射影向量的模, 即d=。‎ 下面举例说明：‎ 例 如图，ABCD是边长为4的正方形，GC面ABCD，GC=2，E、F分别是AD、AB的中点，‎ 求点B到平面EFG的距离。‎ C G D B A E F Y Z X 解析：如图，建立空间直角坐标系，则G（0，0，2），B（0，4，0），A（4，4，0），D（4，0，0），E（4，2，0），F（2，4，0）‎ ‎ =（4，2，-2），=（2，4，-2），=（0，4，-2）‎ 设=（x,y,z）是平面EFG的一个法向量 ‎ ∵ =4x+2y-2z=0‎ ‎ ∵ =2x+4y-2z=0‎ ‎ ∴ 可取=（1，1，3）‎ ‎ ‎ 从以上四例我们看到法向量在求角与距离中有独特的优势，解答步骤基本相同:①建立空间直角坐标系；②求出相关点、向量的坐标；③求出平面的一个法向量的坐标④代入公式计算出角或距离。格式化明显，也不用说明（或证明）所作出角或线段就是所求的角或距离，学生易理解和常握。以上四例事实上都是用了坐标法，应注意：坐标法的关键是建立好的空间直角坐标系，每个需要的点的坐标易求，且点的坐标要表示正确，要会求平面的法向量，诸多计算要过关，因此在平常的数学教学中要加强运算能力的培养。应严格要求学生、注意运算的速度和准确性的培养。另外有关两个平面的位置关系，例如垂直或平行，通过平面的法向量的垂直或平行说明，也较易操作，可避开了各种辅助线的添加的难处。‎ ‎1.3 用基向量解决立体几何问题 前面我们用坐标法解决了许多问题,并且学生也最容易想到这种方法。但是用坐标法解决立体几何问题也不总是最好的。如对非规则几何体中的有关问题，在建立坐标系、确定坐标、运算等环节上，就不那么顺利了。即使是最常见的正方体，有时也不便解决。下面看一个例子：‎ 例 （2004年江苏省高考题）在棱长为4的正方体ABCD—A1B1C1D1中，O是正方形A1B1C1D1的中心，点P在CC上，且CC=4CP。‎ （I） 略；‎ （II） 设O点在平面DAP上的射影是H，求证：DH O H P A1‎ A B1‎ C1‎ D1‎ B C D （III） 略。‎ ‎ ‎ 对于第(II)问,如果建立空间直角坐标系,用坐标法来计算的话,一般都要计算出H的坐标,这是有较大困难的，学生往往卡在这里。实际上，取一个基底，用基向量就易解决。‎ 第(II)问解法如下：‎ 设 由题设可知 ‎∴‎ ‎ ‎ ‎ ‎ ‎ ‎ 故DH。‎ 本例也可用坐标法解答，下文将阐述。‎ 选定空间不共线的三个向量作为基向量，并用它们表示出指定向量，再进行计算,也能巧妙的解决许多立体几何问题。特别是对非规则几何体且相关向量都能用基向量表示的有关问题,常常能有突破。‎ ‎1.4、正确处理传统方法与向量法代数推理之间的关系 高二（下B）教材引入空间向量，是引导我们要将教学的重点放在培养学生使用向量代数方法解决立体几何问题的能力，这一点是毋庸质疑的。空间向量在平行、垂直关系的论证，空间角和距离的计算上有着独特的优势，它很大程度上避开了思维的高强度转换，避开了各种辅助线添加的难处，代之以空间向量的计算；而空间向量的坐标运算，更使得艰涩繁杂的立体几何问题变的思路顺畅，运算简单。特别是用数量积求异面直线所成的角，斜线和平面所成的角，二面角的平面角，用向量在法向量上的投影求点到平面的距离，异面直线间的距离，两平行平面间的距离等问题，体现了向量解法的强大功能。‎ 可是传统的方法是不是就完全摈弃呢？回答是否定的，减弱、淡化综合推理的训练，并不等于完全不要。本章虽然加进了空间向量 ，但学生学习立体几何的基本要求、空间想象能力的培养是不能降低的。平面的基本性质、空间线面平行垂直的各个性质都是研究立体几何的重要基础，空间概念的建立、空间想象能力、逻辑思维能力的培养也是由此开始并逐渐得到发展，而且也是空间向量学习的基础。所以我们在教学中要把几何综合推理和向量代数运算推理有机地结合起来，为多角度的展开解题思路提供广阔的空间，不能有所偏废。下面举例说明：‎ 例 （本例同上例）在棱长为4的正方体ABCD—A1B1C1D1中，O是正方形A1B1C1D1的中心，点P在CC上，且CC=4CP。‎ （I） 略；‎ （II） 设O点在平面DAP上的射影是H，求证：DH （III） 略。‎ O H P A1‎ A B1‎ C1‎ D1‎ B C D 图1‎ X Y Z O H P A1‎ A B1‎ C1‎ D1‎ B C D 图2‎ ‎ ‎ 以上已分析了用坐标法不易解答该题，主要原因是点H的坐标不易求出，但点0的坐标易求，而OH平面APD，连结OD，由三垂线定理的逆定理可知：欲证DH，只须证DO，这用坐标法易做到。‎ 第(II)问解法如下：‎ 如图2，建立空间直角坐标系，其中D为坐标原点，则D（0，0，4），‎ O（2，2，4），A（4，0，0），P（0，4，1）‎ ‎∴‎ ‎∴=８－８＋０＝０‎ ‎∴‎ ‎∴DOPA 由三垂线定理的逆定理可知:．‎ 由此可见，传统方法与向量法有机地结合起来，才是最佳。传统方法有它的优越性，一旦空间的位置关系搞清楚了，计算量较小，正确率高。因此在日常训练中，就应该引导学生养成良好的思维习惯，从多个角度思考问题，不能让思维陷入模式化的僵局。在处理具体问题时，要采取实事求是的态度：凡是用向量比较容易解决的问题 ，就以向量为“通法”来解决；而对有些直接使用线面关系性质定理、勾股定理和三角知识比较容易解决的问题 ，仍用传统方法去对待。‎ 总之，向量是解决立体几何问题的一种得力工具。不少复杂的几何推理，可借助向量使其模式化，用机械性操作加以实现。借助向量可避开一些麻烦的推理和辅助线的添加，使解答过程顺畅、简捷。特别求角和距离、证明平行和垂直上，体现了向量解法的强大功能。对于常见的正方体、长方体、正棱柱、正棱锥，由于容易建立空间直角坐标系和确定坐标，以算代证的优势容易体现。培养和发展学生的逻辑思维能力是教学立体几何的重要任务，因此，传统的方法也不能放弃，应注重二者的有机结合，使之相互呼应，相得益彰。‎ A B C D D1‎ A1‎ B1‎ C1‎ E F 图5‎ 例1、如图5 , 在棱长为a的正方体ABCD－A1B‎1C1D1中，E、F分别是棱BC、CD上的点，且BE＝CF．求异面直线B‎1F与D1E所成的角； 　‎ A B C D D1‎ A1‎ B1‎ C1‎ E F x y z G 图6‎ 解：以A为原点，分别以为x轴、y轴、z轴建立空间直角坐标系，如图6 　　设BE＝x，则有B1(a，0，a)，D1(0，a，a)， E(a，x，0)，F(a－x，a，0) 　　‎ ‎∴ 　　∴ 　　因此，B‎1F⊥D1E．即 B‎1F与D1E所成的角为90 ‎ A B C D D1‎ A1‎ B1‎ C1‎ E F 图7‎ 说明：‎ 本题也可利用线面垂直来证明B1F⊥D1E，也可通过平移直接求异面直线B1F与D1E所成的角，如图7，连接BF、AE、A1D、AD1，在正方形ABCD中，由BE=CF可证得BFAE，又BF为B1F在底面ABCD上的射影，B1FAE，又 B1F在面A1ADD1上的射影为A1D，而A1DAD1， B1FAD1，又AD1AE=A，B1F面AED1，而D1E面AED1 B1F⊥D1E。 ‎ 显然，利用此法比利用向量解要复杂的多，本题充分体现了利用向量法解决立体 A z y B x F E P D C 图8‎ 几何问题的优越性。‎ 例2、如图8，四棱锥P - ABCD中，PD底面ABCD，底面ABCD是直角梯形，BAD = ADC = 90，AB = AD = PD = 2，CD = 4，E是PB的中点，以DA、DC、DP分别为x轴、y轴、z轴建立直角坐标系。‎ （1） 若点F平面ABCD，且FE面PBC，，求F点坐标；‎ （2） 求直线AB与平面PBC所成的角。‎ 解：依题意，知A（2，0，0），B（2，2，0），C（0，4，0）, P (0,0,2)‎ ‎ F平面ABCD，故可设F（x，y，0）‎ 又E（1，1，1），= （x –1，y–1，–1）‎ ‎ FE面PBC， , ‎ 又=（2，2，–2），=（0，4，-2）‎ 于是 ‎ 解得，故F（）‎ （2） 由（1）知，为平面PBC的法向量，‎ ‎= （），又 =（0，2，0），‎ ‎ cos=‎ ‎=‎ ‎==‎ cos= ‎ 设AB与平面PBC所成的角为, 则有= ,‎ sin= cos=‎ 即AB与平面PBC所成的角为arcsin.‎ 说明：‎ 本例中，按常规方法。求AB与平面PBC所成的角，需找AB在平面PBC内的射影，而过A点作平面PBC的垂线，垂足的位置不易找到，利用向量来解，巧妙地绕过了这一难点，问题迎刃而解。‎ z x y C B A A1‎ B1‎ P C1‎ 图9‎ 例3、如图9，正三棱锥ABC—A1B1C1的所有棱长均为2，P是侧棱AA1上一点。‎ （1） 当BC1B1P时，求线段AP的长；‎ （2） 在（1）的条件下，求二面角C—B1P—C1的大小。‎ 解（1）以A为原点，以AB为y轴,AA1为z轴,过A且与平面ABB1A1垂直的直线为x轴建立空间直角坐标系，如图,设AP = m, 则有 B(0,2,0),C() , C1(), B1(0,2,2) , P(0,0,m),‎ ‎=(), =(0, -2 , m –2)‎ BC1B1P, = 0‎ ‎ ,‎ 解得m = 1，即线段 AP的长为1。‎ ‎（2）侧面BCC1B1为正方形， B C1B1C 又 B C1B1P， B1P B1C=B1‎ ‎ B C1平面B1PC ，‎ ‎ B C1为平面B1PC 的法向量，‎ 且 =（），‎ 平面的法向量不唯一，‎ 故不妨设平面B1PC1的法向量为=（x，y，1）‎ 则， ‎ 又= (0, -2 ,–1)，=（）‎ 解得 β α b a B A 图10‎ 即平面B1PC1的法向量为（。 ‎ ‎ cos=‎ ‎ ==‎ 二面角C1—B1P—C有大小为arccos。‎ 说明：‎ ①第二问可直接作出二面角的平面角；设B‎1C与BC1的交点为O，则C1O面 B1PC；过C1作B1P的垂线，垂足为E , 连OE，则OEC1即为二面角的平面角。‎ ②若= （x，y，z）是平面的法向量，如果无其它条件限制，有无数个，而与内两相交直线垂直 , 故只能列出关于x、y、z的两个方程，因此只能求出其中的两个，为方便，我们这里设法向量=（x，y，1），当然也可以设法向量为=（x，2，z）、=（0，y，z）等。‎ 一、 ‎ 利用空间向量求距离 x y A C11‎ B C D A1‎ B1‎ D1‎ z 图12‎ 例4、如图12，在正方体ABCD—A1B1C1D1‎ 中，棱长为1，求异面直线AB1与BD之间的距离。‎ 解：建立如图的直角坐标系，连接A1C，A1B，‎ AC由三垂线定理知，‎ A‎1CB‎1A ， A‎1CBD 又A1（0，0，1），C（1，1，0），‎ 而AAB，BBD，=（1，0，0），‎ 异面直线A1B与BD间的距离 B A C P E F 图13‎ d = = =‎ 例5、如图13，已知边长为的正三角形中，、分别为和的中点，面，且，设平面过且与平行，求与平面间的距离.‎ 解：设、、的单位向量分别为、、，选取{，，}作为空间向量的一组基底，易知 ‎，‎ ‎===，‎ N Q P M C D A A1‎ B B1‎ C1‎ D1‎ 图14‎ 设是平面的一个法向量，则，‎ ‎，‎ 即，‎ 直线与平面间的距离=‎ 例6、如图14，已知正四棱柱ABCD—A1B‎1C1D1的底面边长为4，A‎1A=6，Q为BB1的中点，PDD1，MA1B1，NC1D1，A‎1M=1，D1N=3，若P为DD1的中点，求三棱锥Q—PMN的体积。‎ 解法（1）：建立如图15的直角坐标系，则 y x z N Q P M C D A A1‎ B B1‎ C1‎ D1‎ 图15‎ 有P（0，0，3），M（4，1，0），N（0，3，0），=，=，=‎ A ‎，‎ COS = ==‎ sinMPN==‎ O R N Q P M C D A A1‎ B B1‎ C1‎ D1‎ 图16‎ 又 =（4，4，0），设平面PMN的法向量为=（x，y，z），‎ 则由 得，‎ y = z = 2x，不妨取=（1，2，2），‎ 则Q到平面PMN的距离h === 4‎ 解法（2）：如图16，连接B1D1，交MN于O，‎ 则O为B1D1的中点，连DB1，由P为DD1的中点知，‎ DB1 // OP 延长D1D至R，使DR =DD1，‎ 连QR，则QB1 // DR，且QB1 = DR 四边形B1QRD为平行四边形，‎ QR//B1D， 又OP//B1D QR//OP ， ‎ QR与面PMN平行，‎ 三棱锥Q—PMN的体积与三棱锥R—PMN的体积相等，‎ 而 = —‎ ‎ D‎1M=， D1N = 3MN = ，‎ ‎=‎ ‎=， =‎ ‎ = — = 18—6 = 12‎ 即A = 12‎ 立体几何中几类典型问题的向量解法 空间向量的引入为求立体几何的空间角和距离问题、证线面平行与垂直以及解决立体几何的探索性试题提供了简便、快速的解法。它的实用性是其它方法无法比拟的，因此应加强运用向量方法解决几何问题的意识，提高使用向量的熟练程度和自觉性，注意培养向量的代数运算推理能力，掌握向量的基本知识和技能，充分利用向量知识解决图形中的角和距离、平行与垂直问题。‎ 一、 利用向量知识求点到点，点到线，点到面，线到线，线到面，面到面的距离 ‎ ‎（1）求点到平面的距离除了根据定义和等积变换外还可运用平面的法向量求得，方法是：求出平面的一个法向量的坐标，再求出已知点与平面内任一点构成的向量的坐标，那么到平面的距离 ‎ （2）求两点之间距离，可转化求向量的模。‎ ‎ （3）求点到直线的距离，可在上取一点，令或的最小值求得参数，以确定的位置，则为点到直线的距离。还可以在上任取一点先求，再转化为，则为点到直线的距离。‎ ‎(4)求两条异面直线之间距离，可设与公垂线段平行的向量，分别是上的任意两点，则之间距离 例1：正方体的棱长为1，求异面直线与间的距离 解：如图建立坐标系，则 z A B C D M N x y z z z z ‎，设是直线与的公垂线，且 则 ‎，‎ 例2：如图，在长方体中，求平面与平面的距离。‎ A B C D x y z 解：，同理又，建立直角坐标系，，‎ ‎,设为平面的法 向量，则 由，‎ 不妨设，再选一条斜线段（端点分别在两个平面内），求斜线段对应的向量在法向量上的射影向量的模即可。‎ 点评：若是平面的法向量，是平面的一条斜线段，且，则点到平面的距离，平行平面之间的距离转化为点到平面的距离，变为斜线在法向量上的射影向量的模。‎ 二、利用向量知识求线线角，线面角，二面角的大小。‎ ‎（1）设是两条异面直线，是上的任意两点，是直线上的任意两点，则所成的角为 ‎ （2）设是平面的斜线，且是斜线在平面内的射影，则斜线与平面所成的角为。设是平面的法向量，是平面的一条斜线，则与平面所成的角为。‎ ‎（3）设是二面角的面的法向量，则就是二面角的平面角或补角的大小。‎ 例3：在棱长为的正方体中，分别是的中点，‎ ‎（1）求直线所成角；‎ A B C D E F G x y z ‎（2）求直线与平面所成的角，‎ ‎（3）求平面与平面所成的角 解：（1）如图建立坐标系，则 ‎，‎ 故所成的角为 ‎（2）所以在平面内的射影在的平分线上，又为菱形，为的平分线，故直线与平面所成的角为，建立如图所示坐标系，则，‎ ‎， ‎ 故与平面所成角为 由所以平面的法向量为下面求平面的法向量，设，由，，‎ ‎，所以平面与平面所成的角 例4：S B A C D z x y 如图，在底面是直角梯形的四棱锥S-ABCD中，∠ABC = 90°，SA⊥面ABCD，SA = AB = BC = 1，．求面SCD与面SBA所成的二面角的正切值． ‎ 解：如图建立直角坐标系，则 ‎，‎ 所以是平面的一个法向量。设平面的一个法向量 由，‎ 令，‎ 平面与平面所成的二面角的正切值为 点评：用向量知识求二面角的大小时，是将二面角的问题转化为两平面的法向量的夹角问题，（1）当法向量的方向分别指向二面角内侧与外侧时，二面角的大小等于法向量的夹角的大小。‎ ‎（2）当法向量的方向同时指向二面角的内侧或外侧时，二面角的大小等于法向量的夹角的补角。‎ ‎ ‎ 三、利用向量知识解决立体几何中的探索性问题。‎ 例5：如图，在四棱锥P—ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E、F分别是AB、PB的中点.‎ ‎（Ⅰ）求证：EF⊥CD；‎ ‎（Ⅱ）在平面PAD内是否存在一点G，使GF⊥平面PCB，并证明你的结论；‎ ‎（Ⅲ）求DB与平面DEF所成角的大小.‎ ‎2、解：以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系（如图），设AD=a，则D（0，0，0）、A（a,0,0）、B(a,a,0)、C(0,a,0)、、‎ ‎（Ⅰ）‎ ‎（Ⅱ）假设存在，‎ ‎（Ⅲ）设平面DEF的法向量为 A D B C D D D 例6：如图，在直三棱柱中，‎ ‎（1）求证（2）在上是否存在点使得 ‎（3）在上是否存在点使得 解：直三棱柱，两两垂直，以为坐标原点，‎ 直线分别为轴轴，轴，建立空间直角坐标系，‎ 则，‎ ‎（1），‎ ‎（2）假设在上存在点，使得，则 其中，则，于是由于，且 所以得，所以在上存在点使得，且这时点与点重合。‎ ‎（3）假设在上存在点使得，则其中则，又由于，，所以存在实数成立，所以，所以在上存在点使得，且使的中点。‎ A B C D D1‎ A1‎ B1‎ C1‎ E F 图5‎ 练习1、如图5 , 在棱长为a的正方体ABCD－A1B‎1C1D1中，E、F分别是棱BC、CD上的点，且BE＝CF．求异面直线B‎1F与D1E所成的角； 　‎ A B C D D1‎ A1‎ B1‎ C1‎ E F x y z G 图6‎ 解：以A为原点，分别以为x轴、y轴、z轴建立空间直角坐标系，如图6 　　设BE＝x，则有B1(a，0，a)，D1(0，a，a)， E(a，x，0)，F(a－x，a，0) 　　‎ ‎∴ 　　∴ 　　因此，B‎1F⊥D1E．即 B‎1F与D1E所成的角为90 ‎ 说明：‎ A B C D D1‎ A1‎ B1‎ C1‎ E F 图7‎ 本题也可利用线面垂直来证明B‎1F⊥D1E，也可通过平移直接求异面直线B‎1F与D1E所成的角，如图7，连接BF、AE、A1D、AD1，在正方形ABCD中，由BE=CF可证得BFAE，又BF为B‎1F在底面ABCD上的射影，B‎1FAE，又 B‎1F在面A1ADD1上的射影为A1D，而A1DAD1， B‎1FAD1，又AD1AE=A，B‎1F面AED1，而D1E面AED1 B‎1F⊥D1E。 ‎ 显然，利用此法比利用向量解要复杂的多，本题充分体现了利用向量法解决立体 几何问题的优越性。‎ A z y B x F E P D C 图8‎ 练习2、如图8，四棱锥P - ABCD中，PD底面ABCD，底面ABCD是直角梯形，BAD = ADC = 90，AB = AD = PD = 2，CD = 4，E是PB的中点，以DA、DC、DP分别为x轴、y轴、z轴建立直角坐标系。‎ （1） 若点F平面ABCD，且FE面PBC，，求F点坐标；‎ （2） 求直线AB与平面PBC所成的角。‎ 解：依题意，知A（2，0，0），B（2，2，0），C（0，4，0）, P (0,0,2)‎ ‎ F平面ABCD，故可设F（x，y，0）又E（1，1，1），= （x –1，y–1，–1） FE面PBC， , 又=（2，2，–2），=（0，4，-2）于是 ‎ 解得，故F（）（2）由（1）知，为平面PBC的法向量，‎ ‎= （），又 =（0，2，0）， cos====cos= 设AB与平面PBC所成的角为, 则有= ,‎ sin= cos=即AB与平面PBC所成的角为arcsin.‎ 说明：本例中，按常规方法。求AB与平面PBC所成的角，需找AB在平面PBC内的射影，而过A点作平面PBC的垂线，垂足的位置不易找到，利用向量来解，巧妙地绕过了这一难点，问题迎刃而解。‎ z x y C B A A1‎ B1‎ P C1‎ 图9‎ 练习3、如图9，正三棱锥ABC—A1B‎1C1的所有棱长均为2，P是侧棱AA1上一点。‎ （1） 当BC1B1P时，求线段AP的长；‎ （2） 在（1）的条件下，求二面角C—B1P—C1的大小。‎ 解（1）以A为原点，以AB为y轴,AA1为z轴,过A且与平面ABB‎1A1垂直的直线为x轴建立空间直角坐标系，如图,设AP = m, 则有 B(0,2,0),C() , C1(), B1(0,2,2) , P(0,0,m),=(), =(0, -2 , m –2)‎ BC1B1P, = 0,‎ 解得m = 1，即线段 AP的长为1。‎ ‎（2）侧面BCC1B1为正方形， B C1B‎1C又 B C1B1P， B1P B‎1C=B1‎ ‎ B C1平面B1PC ，B C1为平面B1PC 的法向量，且 =（），‎ 平面的法向量不唯一，故不妨设平面B1PC1的法向量为=（x，y，1）‎ 则， 又= (0, -2 ,–1)，=（）‎ 解得 即平面B1PC1的法向量为（。 cos=‎ ‎ ==二面角C1—B1P—C有大小为arccos。‎