2020年高考真题——数学（海南卷） Word版含解析 14页

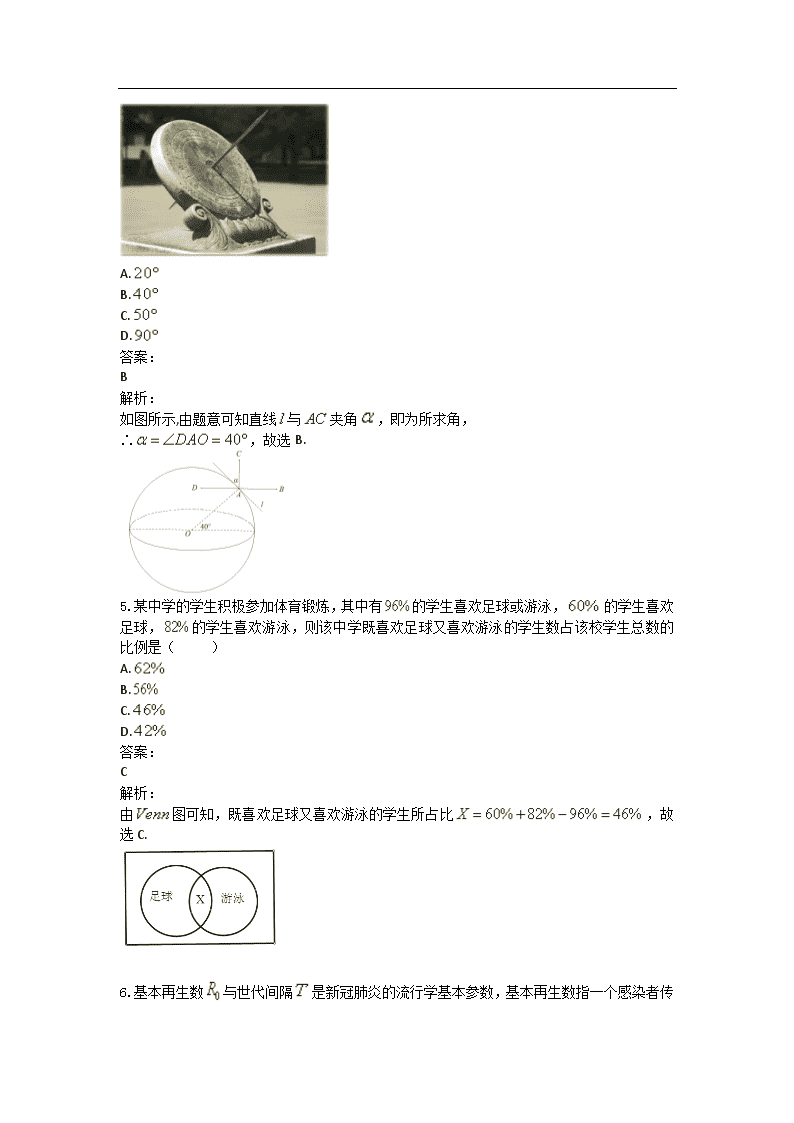
2020 年普通高等学校招生全国统一考试（海南卷） 数 学 1.设集合 ， ，则 （ ） A. B. C. D. 答案： C 解析： 由题可知 ，∴选 C. 2. （ ） A. B. C. D. 答案： D 解析： . 3. 名同学到甲、乙、丙三个场馆做志愿者，每名同学只去 个场馆，甲场馆安排 名，乙 场馆安排 名，丙场馆安排 名，则不同的安排方法共有（ ） A. 种 B. 种 C. 种 D. 种 答案： C 解析： . 4.日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时 间，把地球看成一个球（球心记为 ），地球上一点 的纬度是指 与地球赤道所在平 面所成角，点 处的水平面是指过点 且与 垂直的平面，在点 处放置一个日晷， 若晷面与赤道所在平面平行，点 处的纬度为北纬 ，则晷针与点 处的水平面所成角 为（ ） { |1 3}A x x= ≤ ≤ { | 2 4}B x x= < < A B∪ = { | 2 3}x x< ≤ { | 2 3}x x≤ ≤ { |1 4}x x≤ < { |1 4}x x< < { |1 4}A B x x∪ = ≤ < 2 1 2 i i − =+ 1 1− i i− 2 (2 )(1 2 ) 5 1 2 (1 2 )(1 2 ) 5 i i i i ii i i − − − −= = = −+ + − 6 1 1 2 3 120 90 60 30 1 2 6 5 60C C⋅ = O A OA A A OA A A 40° A A. B. C. D. 答案： B 解析： 如图所示,由题意可知直线 与 夹角 ，即为所求角， ∴ ，故选 B. 5.某中学的学生积极参加体育锻炼，其中有 的学生喜欢足球或游泳， 的学生喜欢 足球， 的学生喜欢游泳，则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的 比例是（ ） A. B. C. D. 答案： C 解析： 由 图可知，既喜欢足球又喜欢游泳的学生所占比 ，故 选 C. 6.基本再生数 与世代间隔 是新冠肺炎的流行学基本参数，基本再生数指一个感染者传 20° 40° 50° 90° l AC α 40DAOα = ∠ = ° 96% 60% 82% 62% 56% 46% 42% Venn 60% 82% 96% 46%X = + − = 0R T 染的平均人数，世代间隔指间隔相邻两代间传染所需的平均时间，在新冠肺炎疫情初始阶段， 可以用指数模型： 描述累计感染病例数 随时间 （单位：天）的规律，指数增 长率 与 ， 近似满足 ，有学者基于已有数据估计出 ， ， 据此，在新冠肺炎疫情初始阶段，累计感染病例数增加 倍需要的时间约为（ ） （ ） A. 天 B. 天 C. 天 D. 天 答案： B 解析： ， ， ，∴ ，得 ，∴ ，∴ ，∴ ， . 7.已知 是边长为 的正六边形 内的一点，则 的取值范围是（ ） A. B. C. D. 答案： A 解析： 如图，建立平面直角坐标系 ，由题意知 ， ， ， ， 设 ，则 ，∵ ，∴ ，∴ 的 取值范围是 . 8.若定义在 的奇函数 在 单调递减，且 ，则满足 的 的取值范围是（ ） A. B. ( ) rtI t e= ( )I t t r 0R T 0 1R rT= + 0 3.28R = 6T = 1 ln2 0.69≈ 1.2 1.8 2.5 3.5 0 3.28R = 6T = 0 1R rT= + 3.28 1 6r= + 0.38r = 0.38( ) 2tI t e= = 0.38 ln 2t = 0.38 0.69t ≈ 1.8t ≈ P 2 ABCDEF AP AB⋅  ( 2, 6)− ( 6, 2)− ( 2, 4)− ( 4, 6)− A xy− (0,0)A (2,0)B (3, 3)C ( 1, 3)F − ( , )P x y 1 3x− < < ( , ) (2,0) 2AP AB x y x⋅ = ⋅ =  2 2 6x− < < AP AB⋅  ( 2, 6)− R ( )f x ( ,0)−∞ (2) 0f = ( 1) 0xf x − ≥ x [ 1,1] [3, )− ∪ +∞ [ 3, 1] [0,1]− − ∪ C. D. 答案： D 解析： ∵ 为 上奇函数，在 单调递减，∴ ， 上单调递减. 由 ，∴ ，由 ，得 或 ， 解得 或 ，∴ 的取值范围是 ，∴选 D. 9.已知曲线 （ ） A.若 ，则 是椭圆，其焦点在 轴上 B.若 ，则 是圆，其半径为 C.若 ，则 是双曲线，其渐近线方程为 D.若 ， ，则 是两条直线 答案： A、C、D 解析： 由曲线 ，得其标准形式为 ， A 中，若 ，则 ，表示焦点在 轴上； B 中，若 ，则 ，表示圆心在原点，半径为 的圆； C 中，若 ，则 ， 异号， 表示双曲线，渐近线方程为 ； D 中，若 ， ，则 ，表示两条直线. 10.右图是函数 的部分图像，则 （ ） [ 1, 0] [1, )− ∪ +∞ [ 1,0] [1,3]− ∪ ( )f x R ( ,0)−∞ (0) 0f = (0, )+∞ (2) 0f = ( 2) 0f − = ( 1) 0xf x − ≥ 0 ( 1) 0 x f x ≥  − ≥ 0 ( 1) 0 x f x ≤  − ≤ 1 3x≤ ≤ 1 0x− ≤ ≤ x [ 1, 0] [1,3]−  2 2: 1C mx ny+ = 0m n> > C y 0m n= > C n 0mn < C my xn = ± − 0m = 0n > C 2 2: 1C mx ny+ = 2 2 11 1 x y m n + = 0m n> > 1 1 n m > y 0m n= > 2 2 1x y n + = 1 n 0mn < m n C my xn = ± − 0m = 0n > 2 1:C y n = sin( )y xω ϕ= + sin( )xω ϕ+ = A. B. C. D. 答案： B、C 解析： 由图易知 ，则 ， ，由题意结合图像知， ， 故 ，则 . 11.已知 ， ，且 ，则（ ） A. B. C. D. 答案： A、B、D 解析： ∵ ， ，且 ，因为 ，∴ ， A： ，A 对， B： ， ，∵ ，∴ ，∴ ，B 对. sin( )3x π+ sin( 2 )3 x π − cos(2 )6x π+ 5cos( 2 )6 x π − 2 2 3 6 2 T π π π= − = T π= 2 2T πω = = 2 6 π ϕ π× + = 2 3 πϕ = 2sin(2 ) sin(2 ) sin( 2 )3 3 3y x x x π π ππ= + = + − = − sin(2 ) cos(2 )2 6 6x x π π π= + + = + 0a > 0b > 1a b+ = 2 2 1 2a b+ ≥ 12 2 a b− > 2 2log log 2a b+ ≥− 2a b+ ≤ 0a > 0b > 1a b+ = 2a b ab+ ≥ 1 4ab ≤ 2 2 2 1 1( ) 2 1 2 2a b a b ab+ = + − ≥ − = 0a > 0b > 1a b+ = 1a b− > − 12 2 a b− > C： ，C 错. D： ，∴ ，D 对. 12.信息熵是信息论中的一个重要概念，设随机变量 所有可能的取值为 ，且 ， ， 定 义 的 信 息 熵 （ ） A.若 ，则 B.若 ，则 随着 的增大而增大 C.若 ，则 随着 的增大而增大 D.若 ，随机变量 所有可能的取值为 ， ，…， ，且 ，则 答案： A、C 解析： A 中：当 时，则 ， . B 中：若 ，由题知 ， ， ， ∴ ，∴B 错误. C 中： ， ， ∴ ， ∴ 随着 的增大而增大，∴C 正确. D 中：令 ，则 ， 2 2 2 2 2log log log log ( ) 22 a ba b ab ++ = ≤ = − 2( ) 2 2a b a b ab+ = + + ≤ 2a b+ ≤ X 1,2, n ( ) 0( 1,2, , )iP X i p i n= = > =  1 1 n i i p = =∑ X 2 1 ( ) log n i i i H X p p = = −∑ 1n = ( ) 0H X = 2n = ( )H X 1p 1 1 ( 1,2, , )p i nn = =  ( )H X n 2n m= Y 1 2 m 2 1( ) ( 1,2, , )j m jP Y j p p j m+ −= = + =  ( ) ( )H X H Y≤ 1n = 1 1p = 1 2 1( ) log 0H X p p= ⋅ = 2n = 1 2 1p p+ = 1 2 1 2 2 2 1 2 1 1 2 1( ) ( log log ) [ log (1 ) log (1 )]H X p p p p p p p p=− + =− ⋅ + − ⋅ − 1 2 1 1 2 1(1 ) [(1 ) log (1 ) log ]H X p p p p− =− − ⋅ − + ⋅ ( ) (1 )H X H X= − 1 1 ( 1, 2,3, , )p i nn = =  1 2 1 2 2 2 2( ) ( log log log )n nH X p p p p p p=− ⋅ + ⋅ + + ⋅ 1 2 2 2 2 1 1 1( ) ( log log log )nH X p p pn n n = − ⋅ + ⋅ + + ⋅ 1 2 2 2 1( ) log lognp p p nn = − + + ⋅ = ( )H x n 1m = 2n = 此时 ， ，此时 ， ∴ ，∴D 错误. ∴正确选项为 A、C. 13. 斜 率 为 的 直 线 过 抛 物 线 的 焦 点 ， 且 与 交 于 ， 两 点 ， 则 . 答案： 解析： 由题抛物线 ，可知其焦点为 ，准线为 ， 如图所示.作 ， ，直线 准线交于点 ， 由 ，∴倾斜角 ，∴ ， 由抛物线定义知： ， ， 又∵ ，∴ 为 中点， ∵ ，∴ ， ∵ ，∴ ，∴ ， ∴ . 14.将数列 与 的公共项从小到大排列得到数列 ，则 的前 项和 为 . 1 2( 1) 1P Y p p= = + = 1 2 1 ( ) ( ) log ( ) 0 j H Y p Y p Y = = − ⋅ ⋅ =∑ 2 2 1 2 1 2 2 2 1 ( ) log ( log log ) 0i i i H X p p p p p p = = − = − ⋅ + >∑ ( ) ( )H X H Y> 3 2: 4C y x= C A B | |AB = 16 3 2: 4C y x= (1, 0)F : 1l x = − AA l′ ⊥ BB l′ ⊥ AB H 3ABk = 60θ =  30A HA′∠ =  | | | |AA AF′ = | | | |BB BF′ = | | 2 | |AH AA′= F AH | | 2MF = | | | | 4HF AF= = 1| | | | | |2BB BF HB′ = = 3 | | 4BF = 4| | 3BF = 4 16| | | | | | 4 3 3AB AF BF= + = + = {2 1}n − {3 2}n − { }na { }na n 答案： 解析： ∵ ， ，∴数列 与 的公共项是 的非 负整数倍加 ，即 ，也就是首项为 ，公差为 的等差数列，∴ ，∴ 的前 项和为 . 15.某中学开展劳动实习，学生加工制作零件，零件的截面如图所示， 为圆孔及轮廓圆弧 所在圆的圆心， 是圆弧 与直线 的切点， 是圆弧 与直线 的切点， 四 边 形 为 矩 形 ， ， 垂 足 为 ， ， ， ， ， 到直线 和 的距离均为 ，圆孔半径为 ，则图 中阴影部分的面积为 . 答案： 解析： 过 作 交 于 ，交 于 ，过 作 交 于 ， 设 ，由已知可得 ， ，∴ ， ∴ ，∴ ， ， ， ∴ ， ， 又∵ ，∴ ，解得 . ∴扇形 面积 ， ， 设圆孔的半径为 ，则半圆孔的面积为 ,则 ，∴阴影部分面积为 ， 23 2n n− 2 1 2( 1) 1n n− = − + 3 2 3( 1) 1n n− = − + {2 1}n − {3 2}n − 6 1 6 1( )k k N+ ∈ 1 6 1 6( 1) 6 5na n n= + − = − { }na n 2(1 6 5) 3 22 n n n n + − = − O AB A AB AG B AB BC DEFG BC DG⊥ C 3tan 5ODC∠ = / /BH DG 12EF cm= 2DE cm= A DE EF 7cm 1cm 2cm 5 42 π + A AM EF⊥ DG M BH P O ON DG⊥ DG N OB OA R= = 5AM = 7DM = 5MG = 45AGM∠ = ° OA AH R= = 2OH R= 2 2MN OP R AP= = = 25 2ON R= − 27 2DN R= − 21 2 2S r ππ′ = = 3tan 5ODC∠ = 25 32 527 2 R R − = − 2 2R = AOB 2 1 135 (2 2) 3360S π π= ⋅ ⋅ = 1 2 2 2 2 42AOHS∆ = × × = r S′ 21 2 2S r ππ′ = = 1 5 42AOHS S S S π∆ ′= + − = + ∴面积为 . 16.已知直四棱柱 的棱长均为 ， ，以 为球心， 为半 径的球面与侧面 的交线长为 . 答案： 解析： 在直四棱柱 中，取 中点为 ， 中点为 ， 中点为 ，由 题意易知 ，又 ，则 面 ，在面 内取一点 ，使 ，且 ，∴ ，又 ， ， ∴以 为球心， 为半径的球面与侧面 的交线是以 为圆心，以 为半径的 圆弧 ，由题意易得 ，故该交线长为 . 17.在① ，② ，③ 这三个条件中任选一个，补充在下面问题 中，若问题中的三角形存在，求 的值，若问题中的三角形不存在，说明理由. 问 题 ： 是 否 存 在 ， 它 的 内 角 ， ， 的 对 边 分 别 为 ， ， ， 且 25( 4)2 cmπ + 1 1 1 1ABCD ABCD− 2 60BAD∠ = ° 1D 5 1 1BCC B 2 2 π 1 1 1 1ABCD ABCD− 1 1BC O 1BB F 1CC E 1 1 1DO BC⊥ 1 1BB DO⊥ 1DO⊥ 1 1BBCC 1 1BBCC P 1//OP BB 2O P = 2 2 1 1 5D P D O OP= + = 1 5DE = 1 5DF = 1D 5 1 1BCC B O 2 FPE 2FOE π∠ = 222 2 π π× = 3ac= sin 3c A = 3c b= c ABC∆ A B C a b c ， ？ 答案： 见解析 解析： ①选条件 ，∵ ，∴ ，∵ ，∴ ， ， ，又 ，即 ，∴ ， ∴ ，得 ， ② 选 条 件 ， ， ∵ ， ∴ ， ， ∴ ， ∵ ，∴ ，∴ ，又 ，∴ ， ③选条件 ，∵ ，∵ ，∴ ， 又 ，∴ ， 得 ，不成立.所以三角形 不存在. 18.已知公比大于 的等比数列 满足 ， . （1）求 的通项公式; （2）记 为 在区间 中的项的个数，求数列 的前 项和 . 答案： 见解析 解析： （1）设公比为 ，∴ ， ，解得 或 （舍）， ∴ . （2）由（1）可得 ，∴ ， ，…， ， ， ∴当 时， ；当 时， ； sin 3sinA B= 6C π= 3ac= 3ac= 3c a = sin 3sinA B= 3a b= 1bc =  6c π= 2 2 2 2 cosa b c ab C+ − = 2 2 2 2 2 1 33 2 3 32b b b bb + − = ⋅ ⋅ = 2 2 1 0b b − = 1b= 3, 1a c= = sin 3c A = sin 3c A = sin 3a C = sin 36a π = 6a = sin 3sinA B= 3a b= 2 3b= 2 2 2 32 cos 36 12 2 6 2 3 122c a b ab C= + − = + − ⋅ ⋅ ⋅ = 2 3c = 3c b= 3c b= sin 3sinA B= 3a b= 2 2 2 2 cosa b c ab C+ − = 2 2 23 3 2 3 cos 6b b b b b π+ − = ⋅ ⋅ 2 23b b= ABC 1 { }na 2 4 20a a+ = 3 8a = { }na mb { }na *(0, ]( )m m N∈ { }mb 100 100S q 3 3 20a a qq + = 3 8a = 2q = 1 2q = 3 3 2n n na a q −= = 2n na = 1 2a = 2 4a = 6 64a = 7 128a = 2m < 0mb = 4 2m> ≥ 1mb = 当 时， ；当 时， ； 当 时， ；当 时， ； 当 时， . ∴ . 19..为加强环境保护，治理空气污染，环境检测部门对某市空气质量进行调研，随机抽查了 天空气中的 和 浓度（单位： ），得下表： （1）估计事件“该市一天空气中 浓度不超过 ，且 浓度不超过 ”的概率. （2）根据所给数据，完成下面的 列联表： （3）根据（2）中的列联表，判断是否有 的把握认为该市一天空气中 浓度与 浓度有关？ 附： ， 答案： 见解析 解析： （1）由表格可得 浓度不超过 且 浓度不超过 的天数 有 天. 8 4m> ≥ 2mb = 16 8m> ≥ 3mb = 32 16m> ≥ 4mb = 64 32m> ≥ 5mb = 100 64m≥ ≥ 6mb = 100 1 2 100 0 2 1 4 2 8 3 16 4 32 5 37 6 480S b b b= + + + = + × + × + × + × + × + × = 100 2.5PM 2SO 3/g mµ 2.5PM 75 2SO 150 2 2× 99% 2.5PM 2SO 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d −= + + + + 2.5PM 75 2SO 150 32 6 18 8 64+ + + = ∴概率为 . （2） （3） . ∴有 的把握认为 的浓度与 浓度有关. 20.如图，四棱锥 的底面为正方形， 底面 ，，设平面 与平面 的交线为 . （1）证明： 平面 . （2）已知 ， 为 上的点，求 与平面 所成角的正弦值的最大值. 答案： 见解析 解析： （1）平面 平面 ， 平面 ，∴ ，∵ 平面 ，∴ ，∵正方形 ，∴ ，又 ，∴ 平面 ，∴ 平面 . （ 2 ） 以 为 原 点 ， ， 为 ， ， 轴 ， 建 立 空 间 直 角 坐 标 系 ， 则 ， ， ， ，设平面 的法向量为 ，点 坐标为 ，∴ ，即 ，令 ，得 ，∴ ，∵ ，∴ ， 64 0.64100 = 2 2 2 ( ) 100 (64 10 16 10) 7.484 6.635( )( )( )( ) 80 20 74 26 n ad bcK a b c d a c b d − × × − ×= = ≈ >+ + + + × × × 99% 2.5PM 2SO P ABCD− PD⊥ ABCD PAD PBC l l ⊥ PDC 1PD AD= = Q l PB QCD PAD∩ PBC l= / /BC APD / /BC l PD⊥ ABCD PD BC⊥ ABCD BC DC⊥ PD DC D∩ = BC ⊥ PDC l ⊥ PDC O DA DC DP x y z (0, 0, 0)D (0,1,0)C (0,0,1)D (1,1,0)B QDC ( , , )n x y z= Q ( , 0,1)t 0 0 DC n DQ n  ⋅ = ⋅ =     0 0 y tx z =  + = 1x = z t=− (1,0, )n t= − (1,1, 1)PB= − 2 2 | | |1 | |1 |sin | cos , | | | | | 1 3 3 3 n PB t tn PB n PB t t θ ⋅ + += 〈 〉 = = = ⋅ + ⋅ +      得 ，令 ，得 ，有 ，得 ，∴ 的最大值为 ，∴ 与平面 所成角 的正弦最大值为 . 21.已知椭圆 过点 ，点 为其左顶点，且 的斜率为 . （1）求 的方程； （2）点 为椭圆上任意一点，求 的面积的最大值. 答案： 见解析 解答： （ 1 ） 根 据 题 意 ， 把 点 代 入 椭 圆 得 到 ① ， 设 ， 又 ，∴ ，代入①式，求得 ，∴椭圆 的方程为 . （2）由题意，可知 的直线方程为 ，设直线 与椭圆相切 于 点 ， ， 联 立 方 程 组 得 ， ，得 ，由题意可知 时， 面积最大， 直线 与直线 距离 ， ，∴ . 22.已知函数 . （1）当 时，求曲线 在点 处的切线与两坐标轴围成的三角形的面积. 2 2 1 2sin 3 3 t t t θ + += + 2 2 1 2 3 3 t ty t + += + 2(3 1) 2 (3 1) 0y t t y− − + − = 24 4(3 1) 0y∆ = − − ≥ 20 3y≤ ≤ sinθ 6 3 PB QCD 6 3 2 2 2 2: 1( 0)x yC a ba b + = > > (2,3)M A AM 1 2 C N AMN∆ (2,3)M 2 2 4 9 1a b + = ( ,0)A a− 3 1 2 2AMk a = =+ 4a = 2 12b = C 2 2 116 12 x y+ = AM 2 4 0x y− + = 2 0x y m− + = N 2 2 2 0 116 12 m x x y y+ − + = =   2 216 12 3 48 0y my m− + − = 2 2144 64(3 48) 0m m∆ = − − = 8m = ± 8m = − AMN∆ 2 4 0x y− + = 2 8 0x y− − = 2 2 | 4 ( 8) | 12 5 51 ( 2) d − −= = + − | | 3 5AM = 1 12 53 5 182 5AMNS∆ = × × = 1( ) ln lnxf x ae x a−= − + a e= ( )y f x= (1, (1))f （2）若 ，求 的取值范围. 答案： 见解析 解析： （ 1 ） 当 时 ， ， ∵ ， ∴ ， 又 ， 则 在 点 处 的 切 线 方 程 为 ， 即 ，令 ，则 ，令 ，则 ，故该切线与两坐标轴围成 的三角形的面积为 . （ 2 ） ∵ ， 即 ， ∴ ， ∴ ， ∴ ， 故 ， 令 ， 则 上 式 转 化 为 ，又 ，∴ 在 单调递增，由 可知总有 ， 则 ， 令 ， 则 ， ∴ 当 时 ， ， 此 时 单 调 递 增 ， 当 时 ， ， 此 时 单 调 递 减 ， ∴ ，∴ . ( ) 1f x ≥ a a e= ( ) ln 1xf x e x= − + 1( ) xf x e x ′ = − (1) 1f e′ = − (1) 1f e= + ( )f x (1, (1))f ( 1) ( 1)( 1)y e e x− + = − − ( 1) 2y e x= − + 0x = 2y = 0y = 2 1x e = − − 1 2 222 1 1S e e = × × =− − ( ) 1f x ≥ 1 ln ln 1( 0, 0)xae x a a x− − + ≥ > > 1 1 lnx xae a − ≥ + lnx e exe a a ≥ lnx ex exxe a a ≥ ln ln ex x aaxxe ee ⋅≥ ( ) xg x xe= ( ) (ln )exg x g a ≥ (*) ( ) ( 1)xg x e x′ = + ( )g x (0, )+∞ (*) ln exx a ≥ x exa e ≥ ( ) x exh x e = (1 )( ) x x e ex e xh x e e − −′ = = (0,1)x ∈ ( ) 0h x′ > ( )h x (1, )x ∈ +∞ ( ) 0h x′ < ( )h x max( ) (1) 1h x h= = 1a ≥